La función de Dirichlet
Trataremos en este post de ver cómo existen situaciones relativamente sencillas para las cuales la integral de Riemann no es aplicable.
Adelantamos que en ciertas situaciones aparecen funciones que no son riemann-integrables, y pusimos como ejemplo un problema de cálculo de probabilidades:
Sea una función real de variable real definida en el intervalo [0,1], de la manera siguiente:
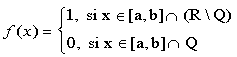
Esta función recibe el nombre de función de Dirichlet.
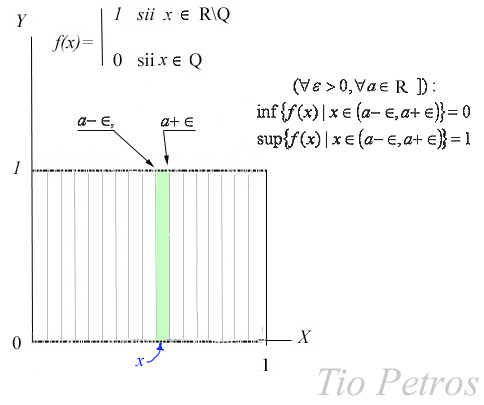
La función vale la unidad para todo punto de [0,1] irracional, y cero para todo punto racional de dicho intervalo. Por lo tanto, la función está definida para todo punto de [0,1].
La representación gráfica de esta función es un poco difícil: entre dos puntos racionales cualesquiera de [0,1] hay infinitos puntos irracionales, y la recíproca también es cierta, así que la gráfica de la función consta de una nube lineal de puntos de ordenada unidad y otra nube lineal de puntos de ordenada nula.
Cuál es el valor esperado de dicho experimento? Un uno es que hemos obtenido un irracional y un cero lo contrario. Cuando hablamos de la insoportable levedad del conjunto Q explicamos que a pesar de la aparente reciprocidad entre Q y R-Q (entre dos irracionales siempre hay infinitos racionales y viceversa), ambos tenían propiedades cardinales muy diferentes: Q es numerable y R-Q tiene la potencia del continuo. Los irracionales contenidos en [0,1] forman un conjunto incomparablemente mayor que los racionales, y esto nos legitima "de alguna manera" a concluir que la probabilidad de que resulte elegido un racional es nula.
Este "de alguna manera" es una vaga invocación a la ley de Laplace de casos favorables entre casos posibles, si bien entre dos conjuntos infinitos la cosa deja mucho de estar clara aunque la intuición resulta (esta vez) ser correcta.
Veamos que la integral de Riemann no nos sirve de gran ayuda en este aspecto. Intentemos integrar la función de Dirichlet por medio de las sumas superiores e inferiores definidas en el post anterior.
A poco que pensemos, vemos que en cualquier elemento de una partición del intervalo [0,1], por muy fina que sea habrá dos clases de puntos: los que tienen la función igual a uno y los que la tienen igual a cero.
Por lo tanto las sumas superiores suman la unidad, mientras que las inferiores son una suma de sumandos nulos, que es nula. No hay por tanto convergencia de las I(f,P) con las S(f,P) del post anterior.
Tenemos que I(f,P)=0 y S(f,P)=1 para cualquier partición P. Por ello I*(f) = 1 ≠ 0 = I*(f) y por lo tanto la función no es Riemann integrable. Como intuimos, la solución a este inconveniente vendrá desde la teoría de la medida...
2 comentarios
mtb -
Maria Teresa Bianchi
Engineer -