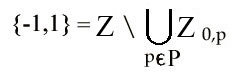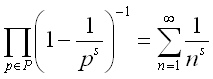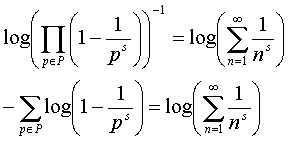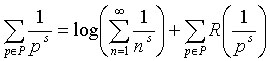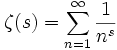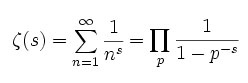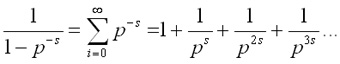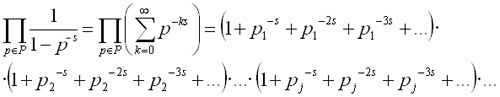Tio Petros

Hay muchos tipos de libros, pero como recordaba Carl Sagan, una vida humana es excesivamente corta para leer una fracción infinitesimal de lo que se publica y hay que elegir. La primera clasificación, obvia donde las haya, es la que separa lo publicado en dos bloques: lo que me interesa y lo que no me interesa. Así no hacemos juicios de valor sobre las obras.

Dentro de lo que me interesa, una separación muy personal pero clara es la siguiente: lo que es accesible para mí y lo que no lo es. Aquí entramos en un terreno muy personal en el que la disponibilidad de tiempo, mi propia preparación, mis prioridades y mi economía tienen mucho que decir. Escojamos pues lo que me interesa y es accesible para mí.

En este clado existen libros que puedo leer en cualquier lugar y libros para los que necesito una cierta parafernalia exterior: hay libros que sólo puedo leer bajo un flexo, envuelto en humo de tabaco y en silencio absoluto e incluso con papel y lápiz cerca para tomar notas; otros son lecturas de verano en tumbona bajo una sombrilla (nunca a pleno sol, por favor).

En este punto la clave de clasificación personal de libros que les muestro, deja de ser dicotómica y se vuelve multivariante. Tengo libros de escritorio, libros para leer en la cama, libros de tumbona, de taberna y de transporte público. Pero quisiera hablar de un tipo de libros que tengo reservado para uno de mis lugares preferidos; el sancta sanctorum del lector: el cuarto de baño.

En mi taxonomía libresca privada clasificar un libro como libro de cuarto de baño es decir mucho sobre el ejemplar en cuestión, y todo bueno: debe ser un libro ágil; de capítulos cortos para poder leer uno entero en el tiempo racional que uno pasa en dicho lugar; debe ser interesante y debe no encajar exactamente en ninguna de las clasificaciones anteriores. Este último punto es importante, porque estoy muy influído por mis lecturas de biología y siempre me ha fascinado la taxonomía y en particular el esfuerzo humano por clasificar la diversidad biosférica en clados anidados, de manera que un clado nunca pertenezca sino a uno y sólo uno de los clados superiores. Así pues, no son para mí libros para leer en ningún otro lugar; y por lo tanto a pesar de lo aparentemente escatológico del asunto este taxón es de absoluta excelencia en lo que a mi respecta. Pocos libros merecen tal categoría.

Así pues, hablemos de los libros para leer en el cuarto de baño. Libros para aprovechar, saborear y disfrutan en cortos espacios de tiempo. Libros cuyos capítulos son joyas que merecen el reposo y la soledad de estos momentos íntimos e intransferibles.

Mi libro actual en estas circunstancias es " Ideas para la imaginación impura ", 53 reflexiones en su propia substancia, de Jorge Wagensberg.

El autor nació en Barcelona en 1948, es licenciado y doctor en Física por la Universidad de Barcelona y profesor de Teoría de los Procesos Irreversibles en la Facultad de Física de dicha universidad, donde dirige un grupo de investigación en biofísica. Es autor de múltiples trabajos científicos aparecidos en publicaciones especializadas internacionales y de una extensa obra de difusión científica hacia otros dominios de la cultura. En 1980 publicó el libro Nosotros y la ciencia (Bosch Editor) y en 1985 Ideas sobre la complejidad del mundo (Tusquets Editores). En 1983 crea la colección de pensamiento científico «Metatemas», también de Tusquets, y desde el año 1991 es director del Museo de la Ciencia de la Fundación ‘la Caixa’.

Tras este cúmulo de avales uno no toma este librito sin esperar algo de mucho interés; de forma que la exigencia a priori es alta. Cincuenta y tres reflexiones en 276 páginas hacen que cada reflexión sea muy cortita en extensión y muy fácil de leer, pero cada una de ellas está llena de bellas implicaciones y reflexiones profundas que se pueden aborar a posteriori. En ellas se muestra al científico como un ser ávido de reflexión y buscador impenitente de fuentes de inspiración en cualquier acontecimiento diario apartentemente trivial.

Un libro en suma excepcional por su interés, digno de un autor que ha demostrado largamente su potencia de divulgador a la vez que su talla de científico, un autor que tituló a otra de sus obras con uno de los títulos más sorprendentes y maravillosos que haya visto nunca; con una frase digna del mejor koan zen: "Si la naturaleza es la respuesta, ¿cuál era la pregunta?" (Colección Metatemas, nº 75; Tusquets editores).

FICHA DEL LIBRO:

TITULO:"Ideas para la imaginación impura, 53 reflexiones en su propio jugo"

AUTOR: Jorge Wagensberg

COLECCIÓN METATEMAS

EDITORIAL: Tusquets Editores

Nada más empezar están los especímenes más conocidos, la base decimal, la binaria y la hexadecimal:

A continuación, están los sistemas basados en una base negativa, gracias a lo cual se pueden representar los números enteros sin tener que indicar su signo. Veamos la base -2:

Observemos cómo los enteros negativos tienen un número par de dígitos, y los enteros positivos un número impar.

Seguimos, y nos encontramos con bases que no son números enteros.

Para comenzar tenemos la base racional 1/10, en la que para convertirla a decimal basta con invertir los dígitos:

Le sigue la base irracional , en la que los números son los mismos que en base 10, pero añadiéndoles ceros entre sus dígitos:

Y ahora, la base , en la que sólo empleamos los dígitos 0 y 1:

Debido a su propiedad , concluimos que en esta base 11=100. Es decir, un mismo número puede representarse de dos formas distintas. Pero recordemos que eso mismo también ocurre en nuestra base diez: 1=0,9999...

Sigamos adentrándonos en el zoo, y vemos ahora la base imaginaria 2i, que emplea los dígitos 0, 1, 2 y 3, y es capaz de representar cualquier número complejo sin ni siquiera tener que indicar su signo:

Cambiando totalmente la dirección de nuestro paseo, llevamos nuestros pasos junto a la base de numeración más antigua y simple, la base 1:

El siguiente sistema posicional más antiguo conocido es el babilónico, de base 60.

Y cerca está la numeración maya. Utilizaban base 20, excepto en astronomía, en la que a partir del tercer dígito en adelante un 20 es cambiado por un 18 (es decir, los multiplicadores son 1, 20, 18×20, 18×20², 18×20³...):

Seguimos, y podemos ver otro sistema de base múltiple, pero que empleamos diariamente: 4 semanas, 5 días, 9 horas, 26 minutos y 8 segundos, son 4₇5₂₄9₆₀26₆₀8 = 2885168 segundos.

Vemos también la base factorial:

Volvemos a cambiar la dirección de nuestros pasos. Hasta ahora, en una base cualquiera b se usan los dígitos 0, 1, 2 y siguientes hasta b-1; en caso de quedarse sin dígitos, se usan letras.

El siguiente espécimen es la base 10 sin cero, en la que para compensar esta carencia se utiliza A=10:

La ya vista base 1 es otro caso de base sin cero.

Igualmente, podemos desplazar la serie de dígitos en sentido contrario, y tener algunos de ellos siendo negativos.

Para la base 3, podemos observar los especímenes basados en (1, 2, 3), (0, 1, 2), (-1, 0, 1) y (-2, -1, 0). Fijémonos en el caso de base 3 balanceada:

Una aplicación común de este último es en balanzas de dos platillos, con pesas que sean múltiplos de 3.

En la base 4 con los dígitos , los números y corresponden ambos al 6.

Después de esto, vienen las bases que emplean más cantidad de dígitos que lo que indica la propia base, que tienen el inconveniente de que los números pueden tener múltiples representaciones. Contemplemos la base 2 con (-1, 0, 1):

Lo siguiente son bases cuyos dígitos no son exclusivamente números enteros, pudiendo tener dígitos que representen números racionales, irracionales, complejos...

Llegamos al final de nuestro paseo y, llevando la vista atrás, sólo nos queda recordar que todos estos sistemas pueden mezclarse entre sí...

Fuentes documentales

Artículos de la Wikipedia sobre Non-standard positional numeral systems.

Siempre he asociado las izquierdas a la racionalidad. Siempre he creído que el pensamiento de la izquierda era, por un lado heredero de las ideas de la ilustración y por otro de la doctrina de filósofos posteriores que se destacaron por su defensa de la razón y del pensamiento científico.

Sin embargo estamos asistiendo a un giro importantísimo de la izquierda hacia el relativismo cultural. Influidos quizás por pensadores francófonos de la talla (baja) de Luce Yrigaray ( La ecuación E = mc², ¿es sexuada? Puede que sí. Supongamos que lo es en la medida en que privilegia la velocidad de la luz frente a otras que nos son menos necesarias), Jacques Lacan (El Organo Eréctil y La Raíz Cuadrada de Menos 1: Así, calculando esa significación según el álgebra que utilizamos, a saber: S (significante) sobre s (significado) = S (el enunciado). Con S=1, tenemos s = Raíz Cuadrada de menos 1. Es así como el órgano eréctil viene a simbolizar el lugar del goce. No en cuanto él mismo, ni siquiera en cuanto a imagen, sino en cuanto parte faltante de la imagen deseada: por eso es igualable a Raíz Cuadrada de menos 1.) o Jean Braudillard (En el espacio euclidiano de la historia, el camino más rápido de un punto a otro es la línea recta, la del progreso y la democracia. Pero esto no es válido nada más que para el espacio lineal de las luces. En el nuestro, el espacio no-euclidiano del fin de siglo, una curva maléfica desvía invenciblemente todas las trayectorias. Ligada sin dudas a la esfericidad del tiempo (visible al horizonte del fin de siglo como aquella de la tierra al horizonte del fin de la jornada) o a la sutil distorsión del campo de gravedad.)…

Influidos, quizás, por tales “pensadores” postmodernos, decía, parece ser que las izquierdas están dando un giro. Es difícil saber hacia dónde. No es hacia la derecha; yo creo que están girando hacia abajo, alejándose de lo que tradicionalmente se ha entendido por pensamiento de izquierdas y deslizándose por un peligroso camino.

El boletín Oficial de las Cortes Generales en su edición del 15 de septiembre del corriente (que lo tienen a su disposición aquí) en su pagina 11 publica la propuesta no de ley 162/00512 con el siguiente título:

PROPUESTA NO DE LEY PRESENTADA POR EL GRUPO PARLAMENTARIO IZQUIERDA UNIDA- INICIATIVA PER CATALUNYA VERDS, sobre la necesidad de regular, de forma consensuada, las terapias naturales, la formación de las mismas y productos naturales pudiendo ser integrados en el sistema sanitario.

En el interior de la propuesta, destacan frases como las siguientes:

"la OMS apoya los tratamientos naturales que tienen que ver con la Naturopatía, la Homeopatía, la Medicina Tradicional China (MTC), así como los tratamientos manuales como la Quiropráctica, la Osteopatía, y por extensión el Masaje Terapéutico, etc. "

¿Es esto verdad?

Veamos lo que dice la OMS por boca de su director general el el Dr. LEE Jong-wook:

«La OMS apoya el uso de las medicinas tradicionales y alternativas cuando éstas han demostrado su utilidad para el paciente y representan un riesgo mínimo, pero a medida que aumenta el número de personas que utiliza esas medicinas, los gobiernos deben contar con instrumentos para garantizar que todos los interesados dispongan de la mejor información sobre sus beneficios y riesgos.» En ese mismo enlace se dice que:

La atención primaria de salud de hasta un 80% de la población de los países en desarrollo se basa en la medicina tradicional, por tradición cultural o porque no existen otras opciones. En los países ricos, muchas personas recurren a diversos tipos de remedios naturales porque consideran que «natural» es sinónimo de inocuo.

La verdadera opinión de la OMS al respecto de las medicinas alternativas es ésta :

Existen datos que parecen avalar el uso de determinadas medicinas tradicionales y complementarias, por ejemplo, la acupuntura para aliviar el dolor, el yoga para disminuir los ataques de asma, o las técnicas de tai ji para ayudar a las personas mayores a disminuir su miedo a sufrir caídas. En la actualidad la OMS no recomienda esas prácticas, pero está colaborando con los países en el fomento de un planteamiento basado en la evidencia para elucidar los cuestiones relativas a la seguridad, eficacia y calidad.

¿Cómo podría ser de otra manera?

La OMS no puede estar de espaldas a un problema de salud a nivel mundial, y se interesa por ello. Sabe que muchos remedios tradicionales son buenos, y explica que apoya el uso de las medicinas tradicionales y alternativas cuando éstas han demostrado su utilidad para el paciente y representan un riesgo mínimo. Es que decir lo contrario sería simplemente idiota: un remedio, natural, tradicional o convencional deberá ser promovido si se demuestra su utilidad, factibilidad y ausencia de efectos secundarios. Si a uste le sienta bien una manzanilla o una tila, tómesela. Sin embargo, las demostraciones caen completamente dentro de la esfera de la ciencia, no de las declaraciones políticas.

Por eso, concluir como hace IU que la OMS da el visto bueno a la homeopatía, es una absoluta barbaridad.

Sigue explicando la propuesta no de ley :

La Administración debe asumir su responsabilidad en la regulación coherente de este sector, de forma consensuada con las partes implicadas, respetando la libertad del ciudadano a elegir libremente la forma que decida para el cuidado de su salud, estableciendo los criterios necesarios que garanticen una mejor seguridad de su salud y de la aplicación de las terapias, basándose en los criterios científicos que conduzcan a un ordenamiento real y justo del sector que beneficie a todas las partes implicadas, en especial del usuario.

Por todo ello se formula la siguiente

PROPOSICIÓN NO DE LEY

El Congreso de los Diputados insta al Gobierno a que constituya un grupo de trabajo, del que formarán parte el Ministerio de Sanidad y Consumo, los grupos parlamentarios con representación en el Congreso de los Diputados y el sector de la salud natural, que culmine con la presentación ante esta Cámara de un proyecto de ley de regulación de dichas terapias con el tiempo suficiente para que sea aprobado en la presente legislatura.

Yo, cuando estoy enfermo lo que reivindico es que me curen de la mejor forma posible. Para ello me pongo en manos de unos profesionales, los médicos. Y no les digo qué tratamiento me deben dar, sino que les pregunto qué tratamiento debo seguir. Si veo que mi gobierno me da la opción de elegir métodos homeopáticos o alopáticos (convencionales) a mi elección, tendré una sensación de libertad, pero perfectamente podré elegir mal.

¿La medicina actual es la mejor de los posibles? Claro que no; pero la única alternativa es una medicina mejor; no una medicina homeopática basada en principios anticientíficos ni una medicina chamánica, por imposición de manos o por apelación a los espíritus de la naturaleza. Allá donde la medicina científica ha ido sustituyendo a estas otras formas espurias de pseudoconocimiento se ha conseguido aumentar la esperanza de vida de los países hasta límiten nunca soñados, así como su calidad de vida.

Izquierda Unida se muestra sorprendentemente cerca de las tesis de la infame revista DSALUD, de los que hablamos aquí y que en uno de sus números declara:

La verdad es que en el largo camino hacia la equiparación con la medicina alopática las otras medicinas encuentran muchos escollos. Entre ellos, el tiempo que deberá transcurrir hasta que se asimilen los nuevos conceptos y enfoques sobre la salud, y se produzca la necesaria modificación de las políticas sanitarias de los distintos estados miembros. Algo más que una aventura.

A lo mejor asistimos en breve a propuestas de ley a favor del curanderismo y de la imposición de manos. Todo ello en aras de un sano distanciamiento de posiciones etnocentristas; como mandan los nuevos cánones idiotas de lo políticamente correcto.

Antes que nosotros, otra cobaya es obligada a elegir a ciegas una de las dos ampollas. La bebe y resulta ser inocua. Ahora nos toca bebermos a nosotros la otra.

La pregunta es la siguiente: ¿nuestra situación es igual, mejor o peor que si simplemente hubiéramos tenido que bebernos la ampolla primera, que tanto podía ser mortal como inocua?

Vayamos paso a paso explicando la situación, y empecemos por poner en común la nomenclatura:

Sea X la elección de la primera persona e Y la elección nuestra.

Llamamos ampolla 1ª a la que ya estaba en la bolsa: de agua pura, y 2ª a la introducida en segundo lugar: la elegida al azar entre dos, una mortal y otra inocua.

Nuestro resultado está afectado por lo que haya sucedido antes: no es lo mismo que el otro cobaya haya tomado la primera ampolla (en cuyo caso quedaría para nosotros la segunda, que puede ser inocua o mortal con equiprobabilidad), que la segunda (en cuyo caso quedaría para nosotros la primera, que es inocua con seguridad). Calculemos la probabilidad a priori de que salvemos la vida en la prueba.

Evidentemente P{X=1ª} = P{X=2ª}=1/2.

Ahora bien, las probabilidades condicionadas por la elección del primero son:

P{Y=inocua /X=1ª}= ½

P{Y=inocua /X=2ª}=1.

Así pues, la probabilidad (absoluta) de que salvemos la vida ( P{Y=inocua}) es:

P{Y=inocua}= P{Y=inocua /X=1ª}· P{X=1ª} + P{Y=inocua /X=2ª}· P{X=2ª}=1/2 ·1/2 + ½ · 1 = ¾.

Por lo tanto tenemos 3 posibilidades de 4 de salvar la vida., y por lo tanto ¼ de morir.

Hemos empleado el teorema de la probabilidad total:

Teorema de la probabilidad total

Sea A₁, A₂, ...,A_n un sistema completo de sucesos tales que la probabilidad de cada uno de ellos es distinta de cero, y sea B un suceso cualquier del que se conocen las probabilidades condicionales P(B/A_i), entonces la probabilidad del suceso B viene dada por la expresión:

Otra forma de hacerlo es dividir el espacio muestral en subsucesos equiprobables y aplicar la regla de Laplace de dividir casos favorables entre posibles.

Efectivamente cuatro son los casos posibles: que nuestro compañero elija la 1ª siendo 2ª inocua, que elija la 1ª siendo la 2ª mortal, que elija la 2ª siendo ésta inocua y que elija la 2ª siendo ésta mortal. Él tiene una posibilidad de cuatro de morir: elegir la 2ª siendo ésta mortal; 1 de 4.

O si queremos, aún podemos calcularno de otra manera, haciendo uso del siguiente teorema:

Si dos sucesos A y B son independientes, entonces la probabilidad de que se den ambos es igual al producto de las probabilidades.

Para que muera el primer elector deben suceder dos cosas: A={que elija la segunda ampolla} y B={que la segunda sea mortal}. Ambos sucesos son independientes de probabilidad ½, luego la conjunción de ambas se dará con la probabilidad producto, que es otra vez ¼.

Así pues, ambos tenemos a priori la misma probabilidad de morir. Esto no debiera parecer extraño: una vez que el primero ha escogido, está clarificado qué ampolla va a tomar cada uno de los dos.

Ahora bien, en nuestro problema estamos preguntando por la probabilidad de que salvemos la vida una vez que sabemos que el primero ha salvado la suya. Ahora las probabilidades a posteriori cambian: sabemos que la posibilidad de que nuestro compañero haya tomado la 2ª, siendo ésta mortal no se ha dado, con lo que quedan tres únicas posibilidades, de las que una nos matará: nuestra probabilidad de morir ahora es 1/3, como había dicho Engineer en los comentarios del post anterior.

Aún así, nuestra situación sigue siendo mejor que si hubiéramos estado obligados a bebernos la ampolla inicial…

Muchas veces lo hemos dicho: los humanos estamos muy mal dotados para calcular probabilidades. Esto es un misterio bastante grande, habida cuenta de lo importante que es en la vida cotidiana tal destreza, pues nos salvaría de un sinnúmero de dificultades. En efecto, no hace falta conocer la Teoría de los Juegos ni el cálculo de riesgos bayesiano para entender que una correcta estimación de las probabilidades es una ayuda inestimable en la vida real. La naturaleza nos debiera haber provisto de una mejor capacidad para ello, dada la mayor probabilidad de incrementar nuestra descendencia en caso de poseer efectivamente tal habilidad. Darwinismo puro y duro que por alguna razón que no entiendo no ha funcionado como aparentemente debiera.

Hablamos de ello aquí cuando dábamos una vuelta de tuerca al famoso problema de Monty Hall, que ha hecho correr ríos de tinta.

También lo mencionamos cuando hablábamos de probabilidades condicionadas y de independencia entre variables aleatorias, aquí y aquí.

Les propongo uno muy sencillo:

En una especie de macabro experimento del que somos las cobayas humanas, vemos como el experimentador escoge al azar entre dos ampollas idénticas llenas de líquido. Nos explican que una contiene un veneno mortal y fulminante, y la otra agua. Repito que la elección se realiza al azar. Dicha ampolla es introducida en una bolsa que ya contenía una ampolla, ésta última de agua pura.

Antes que nosotros, otra cobaya es obligada a elegir a ciegas una de las dos ampollas. La bebe y resulta ser inocua. Ahora nos toca bebermos a nosotros la otra.

La pregunta es la siguiente: ¿nuestra situación es igual, mejor o peor que si simplemente hubiéramos tenido que bebernos la ampolla primera, que tanto podía ser mortal como inocua?

Les espero.

Se ha comentado mucho en la blogosfera, pero nunca será lo suficiente. Ahora que han caído en mis manos me parece un buen momento para comentarlo en Tio Petros, la bitácora de matemáticas que languidece porque su autor no escribe en ella, mientras que sus visitas inexplicablemente siguen aumentando llegando a casi al millar diario.

Ha salido a la arena una colección valiente cuando las soplapolladas venden más que nunca, cuando las míseros códigos Da Vinci son best sellers, cuando la tontería ha invadido los escaparates de nuestras librerías, un puñado de quijotes lanza la colección ¡Vaya timo!

La Editorial Laetoli en colaboración con la Sociedad para el Avance del Pensamiento Crítico bajo el nombre ¡Vaya timo! va a ir tratando esas historias que a menudo nos intentan colar sin ningún tipo de fundamento, o lo que es peor, bajo el amparo de algún tipo de pseudociencia; los tres primeros libros de la colección tratan de OVNIS, la sábana santa y el creacionismo.

El hecho de que el autor de uno de ellos (el de la sábana supuestamente santa), Félix Ares de Blas sea amigo personal mío, además de maestro admirado en lides escépticas ha hecho que no me haya sorprendido en absoluto cuánto pueden dar de sí diez euros. Los otros dos libros prometen la misma calidad.

¿Qué esperas para comprarlos?

Hagamos guerra a la tontería comprando los volúmenes que la editorial Laetoli se ha atrevido a publicar cuando lo que vende es lo contrario.