Demostración topológica de la infinitud de los primos (y 2)

Cumplamos con lo prometido en el post anterior.

Habíamos demostrado dos propiedades importantes en la topología en la que estábamos trabajando:

1.- Todo abierto no vacío es infinito

2.- Todo conjunto de la forma Z_a,b es cerrado, además de abierto.

Según esto, nada nos costará convencernos de que el conjunto formado por los puntos 1 y -1; B={-1,1} no puede ser abierto: es un conjunto finito (sólo tiene dos elementos), y todo abierto diferente del vacío es infinito según la propiedad 1.

Por otro lado, estos dos enteros (el -1 y el 1) son los únicos con los que nos quedaríamos si al conjunto Z le vamos quitando conjuntos de la forma Z_0,p con p, primo mayor que la unidad. En efecto, cada Z_0,p no es sino el conjunto de los múltiplos del primo p, con el cero incluido. Recorriendo todos los primos está claro que nos llevamos todo el Z excepto precisamente los dos puntos citados -1 y 1.

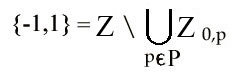
Ahora bien, todos los citados Z_0,p son cerrados por la propiedad 2, y si efectuamos una suma finita de cerrados, seguimos teniendo un cerrado. La única forma de mantener la posibilidad de que {-1,1} no sea abierto es que la unión de todos los Z_0,p no sea cerrada; y para que esto ocurra es necesario que la unión sea infinita. (Recordemos que la unión de infinitos cerrados sí puede ser abierta).

A riesgo de ser repetitivo, y para que se entienda bien, lo volvemos a explicar: si el conjunto de primos fuera finito, entonces la suma de todos los Z_0,p sería un cerrado, y {-1,1}, por ser complementario de un cerrado, sería un abierto; en franca contradicción de la propiedad 1, que nos asegura que {-1,1} no puede ser abierto por ser finito diferente del vacío.

Luego el conjunto de los números primos es infinito.

Es sorprendente la manera que tienen los números primos de entrar en este discurso. En todo el post anterior no hicieron acto de presencia, y ahora , de un plumazo los tenemos encima. ¿No podríamos haber hecho lo mismo con conjuntos N_0,p en los que p no fueran precisamente primos?

Algún lector se anima a responder a esta pregunta?

29/03/2006 16:38

Comentarios » Ir a formulario

Autor: Lola

ooooooole! Jajaja, ¡qué bueno! Me estoy planteando ponerlo en el único tema en el que puedo meter algo de topología como ejemplo...

Y en cuanto a la pregunta del final... me reservo la resupesta a modo de acertijo! (y le quito el primo 23 y me quedo pululando en el infinito, ea).

Fecha: 29/03/2006 17:33.

Autor: Anabel

El conjunto de los p para que me queden sólo el +1 y el -1 tiene que ser exactamente el de los primos, en caso contrario no quedarían sólo esos dos.

Fecha: 29/03/2006 18:14.

Autor: Tio Petros

La frase que has escrito, Anabel; no es cierta.

Fecha: 29/03/2006 18:29.

Autor: Lola

si hay que añadir, se añade... pero añadir pa na es tontería :P

Fecha: 29/03/2006 20:10.

Autor: Tio Petros

Esa es mi Lola.

Fecha: 29/03/2006 21:53.

Autor: omalaled

Creo que sí puedes hacer lo mismo que dices con N0,p donde p no fuera precisamente número primo, lo que pasa es que demuestras una cosa evidente y es que el número de números no precisamente primos también es infinito.

¿Apruebo?

Salud!

Fecha: 30/03/2006 13:41.

Autor: TioPetros

El conjunto de los p necesarios para quitar a Z todos sus elementos excepto los {1,-1} por sustracción conjuntística de los correspondientes N0,p no es un conjunto definido. Hay infinitos conjuntos que hacen esto, pero la intersección de todos ellos es el conjunto P de los primos.

Dicho de otra manera: el conjunto P de los primos es el menor conjunto que cumple la propiedad citada. Sólo asegurando que para todo primo el conjunto N0,p está sustraido de Z podemos asegurar que sólo nos queda el conjunto {1,-1}.

Como todos estos conjuntos deben ser infinitos, el conjunto P, aún siendo el menor de todos ellos es infinitos. Que la sustracción la hagamos sobre conjuntos mayores que P es posible, pero inútil.

Por eso decía Lola que "si hay que añadir, se añade... pero añadir pa na es tontería".

Fecha: 30/03/2006 19:14.

Autor: Tio Petros

Omalaled, apruebas, apruebas.
Con nota.

Fecha: 01/04/2006 07:29.

Autor: Lola

Pero que digo yo.... si nos falta, digamos, el primo 23... ¿Cómo se consiguen 23, 23^2, 23^3... 23^n....? Es decir el complementario no sería finito y no se podría deducir que la unión hubiera de ser infinita...no? :

Fecha: 01/04/2006 10:00.

Autor: Tio Petros

Hola Lola. Se me había pasado tu último comentario, perdona.

Si tenemos todos los primospero nos falta uno, por ejemplo el 23, entonces el conjunto que nos quedará será infinito pues constaría e los elementos +1, -1 y de todos los múltiplos de 23, que obviamente son infinitos.

Por eso digo que los p pueden estar extendidos a múltiples subconjuntos diferentes de N para que sólo queden al final los elementos {+1,-1}, pero todos ellos deben incluir al conjunto P de los primos.

El complementario no sería finito, con lo que no podríamos afirmar que no puede ser abierto. Un conjunto finito en este topología no lo puede ser, pero uno infinito puede serlo o no serlo. Esto responde a tu pregunta?

Fecha: 03/04/2006 08:23.

Autor: Lola

No, sólo estaba pensando en alto sobre el comentario de omalaled, que yo no lo daba por aprobado, pero vamos, que es un comentario que casi sobra :P

Fecha: 03/04/2006 10:59.

Autor: omalaled

Vaya, Lola ... tendré que repetir post :)

Salud!

Fecha: 03/04/2006 16:56.

Autor: Lola

jajaja, igual el Tío Petros te hace comentar n veces en cada post o algo así... :D

Fecha: 03/04/2006 17:40.

Autor: mewt

Que agradable sorpresa tenerte de vuelta, Tio Petros! Creía que te habías retirado definitivamente de esto del blogueo...
Muy bonita la demostración. Después de ver la primera parte pensaba que ibas a usar el teorema de Dirichlet para sucesiones aritméticas, pero la simplicidad de la demostración que das es sorprendente...
Lola, ¿te animas a buscarle propiedades interesantes a esta topología?, por ejemplo, dado un conjunto finito de enteros {a1,...,an} ¿cuál es el menor abierto que los contiene? ¿Es una topologia T1? ¿Cuáles son los conjuntos densos?

Fecha: 08/04/2006 15:24.

Autor: sergio