Tio Petros

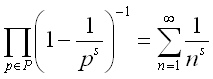
Tomamos logaritmos a ambos lados de la expresión anterior:

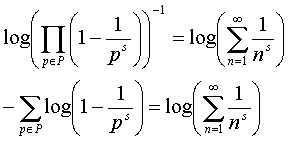
Ahora nos conviene sustituir la función log(1-x) por su desarrollo en serie de Taylor; donde x = 1/p^s < 1/2.  Haciendo dicha sustitución y englobando los términos a partir del segundo en un resto R(1/p^s) ≈ O(1/p^s₎2 obtenemos:

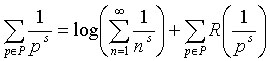
Hagamos s→1. El primer término del segundo miembro es el logaritmo de la serie armónica y por lo tanto es infinito. El segundo término está sin embargo acotado en virtud del orden cuadrático del resto, por lo tanto la suma total es infinita, y de ello deducimos que el primer miembro, que no es sino la suma de los recíprocos de los primos, también es infinita.
Evidentemente esto sólo puede ocurrir si el número de primos es a su vez infinito.

A modo de nota al margen, la posible convergencia de esta suma de recíprocos no hubiera demostrado la finitud de los primos, mientras que la implicación contraria está clara. Un caso de este estilo es el que ocurre con los primos gemelos, que son aquellos primos que distan dos unidades, como el 3 y el 5. Se sabe que la suma de sus recíprocos es convergente, pero aún se desconoce si existen infinitos de ellos. En su día hablamos de ello aquí

En los próximos días hablaremos de otra demostración de lo mismo (de momento la última). Esta es verdaderamente sorprendente, porque utiliza argumentos exclusivamente topológicos (¿Me lees, Lola?).

Al igual que ésta, la desmenuzaremos hasta el límite, necesitando para ello otros dos post. Espero que el paseo les resulte agradable.