Euler y el problema de Basilea
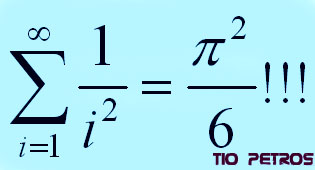Las admiraciones de la fórmula que encabeza este post no son factoriales: son simples exclamaciones que reflejan la sorpresa que produjo en el mundo matemático el descubrimiento de Euler.Hemos contado cómo las mentes de los dos hermanos Bernoulli unidas no fueron suficiente para desentrañar el misterio de la serie de los inversos de los cuadrados 1+1/4+1/9+1/16+...
En un post anterior escribíamos:
Los hermanos Bernoulli, ebrios de gozo por la demostración conseguida (la divergencia de la serie armónica), intentaron conocer los misterios de otra serie: la suma infinita de los inversos de los cuadrados perfectos: 1+1/4+1/9+1/16+1/25+...
Sin embargo, el genio de ambos hermanos juntos era insuficiente para desentrañar el misterio. La serie era convergente,pero...hacia qué número real convergía? Fué necesario el cerebro del maestro de todos los matemáticos para desentrañar el misterio, en un alarde de magia euleriana casi sin parangón en la historia de la matemática.
Mengoli y Leibniz se habían estrellado antes, y ahora los Bernoulli admitían la derrota:
Grande será nuestra gratitud si alguien encuentra y nos comunica lo que hasta ahora ha escapado a nuestros esfuerzos , escribía Jakob Bernoulli en su Tractatus.
Como escribió en Basilea, el reto lanzado fue conocido en su tiempo como el problema de Basilea
Por desgracia para él, moría sin que nadie hubiera podido avanzar en el tema. Hacía falta no uno de los grandes, sino el más grande del momento para recoger el guante y triunfar donde los demás habían fracasado.
Cuando Euler publicó el resultado, el hermano de Jakob, Johann escribió: Utinam Frater superstes effet! (Si viviera mi hermano!). Y no era para menos. La sorpresa por ver el problema de Basilea resuelto quedaba en nada ante la perplejidad del resultado. PI CUADRADO SEXTOS !!!
La irrupción de la constante pi en un lugar tan inesperado no era normal. Según la matemática ha ido avanzando, hemos visto aparecer nuestra querida constante en muchos sitios, pero aquella vez era una de las primeras, y la sorpresa era grande. Sorpresa sí, pero no incredulidad. Se habían sumado más de mil términos de la serie, obteniendo el valor de 1.64393 . Se sabía que la convergencia era lenta, pero pi cuadrado sextos era el valor buscado, sin duda alguna (1.1.6449340...)
En 1.735, Euler escribía pletórico de felicidad: ...Sin embargo, he encontrado ahora y contra todo pronóstico una expresión elegante para la suma de la serie 1+1/4+1/9+1/16+etc., que depende de la cuadratura del círculo... He encontrado que seis veces la suma de esta serie es igual al cuadrado de la longitud de la circunferencia cuyo diámetro es la unidad
¿Cómo consiguió el mago de los números obtener el resultado?
Apartándonos un poco de la tónica general del blog, en el siguiente post describiremos exactamente cómo lo hizo. Como en otras ocasiones, he intentado poner un enlace de algún lugar de la web en el que se explique; pero no lo he encontrado. Así que lo describiremos aquí. Esto no debiera intimidar a nadie: si el lector no puede o no le apetece seguirlo, que ignore el post olímpicamente, pues esto no va a ser un cambio en la tónica general del blog, sino una excepción, que además me permitirá comprobar si puedo insertar con buenos resultados fórmulas propias en medio del texto de un post.
Les espero para mostrarles el mejor Euler en acción sacándose del sombrero una perla de belleza infinita.
______________________________________________________________________
Como siempre pasa en matemáticas, desentrañar un misterio sólo sirve para encontrar otros mucho más difíciles. Efectivamente, la pregunta siguiente era obvia: qué pasa si el exponente de los denominadores no es 2? Y si es cualquier valor real? Y el colmo de la perversión: y si es cualquier valor complejo?
Esta última audaz pregunta dió paso a uno de los objetos más complicados de la matemática (modernos fractales incluidos!!!); la función zeta de Riemann . Pero, como decía Michael Ende, esta es otra historia y deberá ser contada en otra ocasión.
4 comentarios
filomates -
Mientras tanto, para completar bibliografía y acceder a documentos sobre el tema recomiendo:
http://parafernaliasmatematicas.blogspot.com.es/2014/11/problema-de-basilea.html
cero -
Carlos -
jose -
Desde luego los matemáticos son magos.