Blogia
Tio Petros

El Teorema de Feuerbach

- Teoremas
El Teorema de Feuerbach El Teorema de Feuerbach ha sido denominado como la joya de la geometría del siglo XIX . Y realmente no es para menos... Les invito a acercarse un poco al sabor de dicho teorema; como siempre, sin demostraciones y sin hacer matemáticas; tan solo paseando agradablemente.

Que tres puntos de un plano pertenezcan a una misma circunferencia no solo no es nada extraordinario, sino que es algo absolutamente obligado; de hecho tres puntos son los que definen una circunferencia. Dicho de otra manera: dados tres puntos no alineados, existe una y solo una circunferencia que pasa por los tres.

Si dados cuatro puntos existe una circunferencia que pasa por los cuatro, tenemos algo por lo menos curioso: existe alguna relación entre ellos que se refleja en la pertenencia común a la misma circunferencia. Según vamos aumentando el número de puntos, más extraordinario es que todos ellos pertenezcan a la misma circunferencia (o que todos ellos equidisten de otro punto), o más especialmente elegidos son dichos puntos. Por eso, la existencia de la circunferencia de Feuerbach es algo insólito.

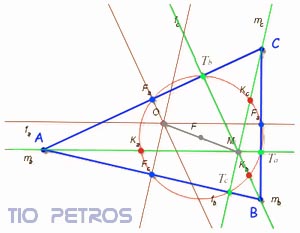
Dado un triángulo ABC cualquiera, las alturas son los segmentos de recta que van desde cada vértice hasta el lado opuesto correspondiente perpendicularmente. En la figura están pintadas de verde. Las tres alturas se concurren en el mismo punto, llamado ortocentro del triángulo (punto M del dibujo). Los puntos de corte de las alturas con los lados del triángulo se denominan pies de las mismas(Puntos Ta,Tb y Tc).

Pues bien: los tres pies de las alturas de un triángulo determinan un círculo, que se llama circunferencia de Feuerbach del triángulo, y recibe también el nombre de circunferencia de los nueve puntos .

Dicha denominación de circunferencia de los nueve puntos proviene del extraordinario hecho de que además de los tres pies citados, también pertenecen siempre a dicha circunferencia los tres puntos medios de los lados del triángulo(puntos Fa,Fb y Fc en el dibujo), y los tres puntos medios de los segmentos que unen cada vértice con el baricentro(puntos Ka,Kb y Kc en el dibujo). Nueve puntos, todos ellos en la misma circunferencia .

En la figura tienen también dibujadas las mediatrices del triángulo (perpendiculares a cada lado por sus puntos medios), que también concurren en un punto: el circuncentro (punto Q en el dibujo). La recta que une ambos puntos, circuncentro y baricentro se denomina recta de Euler . Precisamente el punto medio del segmento QM (punto F) es el centro de la circunferencia de Feuerbach (Dibujado en gris).

Pues bien, esto no es todo: el Teorema de Feuerbach afirma que la circunferencia de nueve puntos es tangente a otras cuatro circunferencias: la inscrita al triángulo y las tres exinscritas.



El punto de tangencia de la circunferencia de Feuerbach (en rojo en la figura anterior) con la inscrita es llamado punto de Feuerbach

Aquí tienen una demostración equivalente al teorema de Feuerbach que no utiliza apenas arsenal analítico.

Belleza en estado puro, ¿no es así?

43 comentarios

jose -

excelente el articulo ya que me permite demostar que el inverso del area del triangulo inscrito es gual a la suma de los inversos de los tres areas de los triangulos exinscritos

Sildenafil -

Tengo que hacer la circunferencia de los nueve puntos, pero no entiendo nada.
Ma podrían explicar paso por paso.

LEONARDO HERNANDEZ -

ESTA TODO MUY BIENO

galois -

comenten sobre el triangulo ortico es un triangulito interesantisimo bastantes propiedades publiquen todas las propiedades en el please

galois -

buenaso el de feuerbach ademas que es uno de los teoremas mas famosos de la geometria

sandra milena -

yo la verdad no se q es eso necesito una explicacion para una exposicion

kenir -

demostracio

Theo -

awer Flácido la recta de Euler esta bien definida en el texto, pero tu tambien la defines bien, ya que la recta de Euler une el circuncentro el baricentro y el Ortocentro

veltham -

odio las matematicas

karla -

me gustaria saber cuales son los teoremas de los angulos de la circunferencia

MAYELA -

no sabe nada ese viejo autor de la página, es un tonto ignorante junto con los que lean esto!

Sirius -

bueno tengo demostrado q la distancia del centro de la circunferencia de los nueve puntos a los nueve puntos
y tambien la de la razon del radio de esta con el radio de la circunscrita por si alguien la kiere ver

neceito luces para demostrar que es tangente a las excinscritas y a la inscrita

YURI -

me interesaria la demostracion de la relacion 1:2 de los radios de la circunferencia de los 9 puntos
y el circunradio del triangulo en referencia

jaume -

felicitats per aquesta pàgina!! parlant d'altures i de triangles... voldria prendrem la llibertat de proposar un tema que es pugui esplicar en aquesta web: la creació d'un triangle a partir de les seves tres altures. Se que és possible, però m'agradaria que expliquesiu el procediment d'una manera sencilla.

jaume -

felicitats per aquesta pàgina!! parlant d\'altures i de triangles... voldria prendrem la llibertat de proposar un tema que es pugui esplicar en aquesta web: la creació d\'un triangle a partir de les seves tres altures. Se que és possible, però m\'agradaria que expliquesiu el procediment d\'una manera sencilla.

merci!

Antonio -

excelentes comntarios y muy buena pagina

Anónimo 10 -

Tengo que hacer la circunferencia de los nueve puntos, pero no entiendo nada.
Ma podrían explicar paso por paso.

GRACIAS...

Anónimo -

Muy Bueno!!!!!!
Sigan Así.

Rescuer -

Muchas gracias por mostrar este teorema... me acabas de sacar de un gran problema matematico.
Es muy buena la pagina, y gracias

Flácido -

Hola otra vez, me acabo de dar cuenta de que el parrafo que habla de la recta de Euler, dice que esta es
la recta que une el circuncentro con el baricentro, y creo que debe dercir que la recta de Euler es la que une
el circuncentro con el ortocentro.

Flácido -

Hola, me temo que para terminar con el pequeño entuerto del baricentro y el ortocentro, todavia hay que corregir el parrafo en el que se explica por que a la circunferencia de Feuerbach se le llama tambien "circunferencia de los nueve puntos". Este parrafo dice que los puntos Ka, Kb y Kc son los puntos medios de los segmentos que unen el baricentro con los vertices del triangulo, pero creo que debe decir que Ka, Kb y Kc son los puntos medios de los segmentos que unen el ortocentro con los vertices.

Anónimo -

arnaldo -

como se llama la union de tres mediatrices

jesus -

Agradezco a tio pretos por la informacion. es la 1 vez q entro y me parece de la PM . Hasta la vista

kenneth -

cual es la demostracion del teorema?

inez -

quiero demostrar q el centro de la Cfa de feiu...es pto medio entre el ortocentro y el circuncentro
??

JIMENA -

holas, alguien me puede mandar una demostracion de que las medianas concurren en el baricentro. GRACIAS

el geometra loco -

Laura, (con su permiso tio PETROS), no se dice "punto de corte", una tijera corta, un serrucho corta, dos rectas NO¡¡, dos rectas se intersecan y no maltrates la geometría.

el geometra loco -

oe cristofer, leete el libro titulado, GEOMETRIA, por Shively.

el geometra loco -

por que un filosofo aleman como feurbach, se interesaria por la geometría?, (su trabajo es excelente tio petros)

Christopher -

Hola, pucha mis respetos, esta bien pero bien piola tu introduccion filosofica.
En la demostración no entiendo lo que es inversión, aqui en el Perú no se lleva eso de inversión =S porfis alguien que me explique

RENE -

EN DONDE PUEDO ENCONTRAR LA DEMOSTRACION DE LA CIRCUNFERENCIA

lauris -

dónde puedo encontrar una demostración de la circunferencia de los nueve puntos, no tan complicada?
gracias..

TioPetros -

Por supuesto que teneis razón. Fué un lapsus que corrijo inmediatamente. Gracias a todos .

Nico -

Hola a todos. Hablando de baricentros y de varios centros, me enseñaron en el cole una regla mnemotécnica para saber en qué centro de un triángulo se cruza qué. Posiblemente muchos la sepáis, pero por si acaso, aquí va. Empleando las palabras MAMBo y BOCIna, e identificando letra a letra por su orden, tenemos que las Medianas se cruzan en el Baricentro, las Alturas en el Ortocentro, las Mediatrices en el Circuncentro, y las Bisectrices en el Incentro. La verdad es que para mí ha resultado ser una regla mnemotécnica "inolvidable". Saludos a todos.

Laura -

me sorprende que aún no hallas corregido el artículo, ya que varios lectores como yo han visto que debe decir que el punto de corte de las alturas es el ortocentro.

Jean Paul -

Ortocentro, sin H y tal como lo dijo Nico.

YUSENT -

Solo quisiera añadir que la recta de euler contiene al hortocentro, baricentro y circuncentro.

YUSENT -

Yo estoy de acuerdo con Nico de hecho es el hortocentro, el baricentro es la interseccion de las medianas (union de un vertice con el punto medio de el lado opuesto a el)

Nico -

Hola. Gracias por la página Tío Petros. Una cosilla: la intersección de las alturas es el ortocentro ¿no?

TioPetros -

Por supuesto!!!

Queda corregido. Gracias.

abc -

Un pequeño comentario...
"el Teorema de Feuerbach afirma que la circunferencia de nueve puntos es tangente a otras cuatro circunferencias: la inscrita al triángulo y las tres circunscritas."

...será las "tres exinscritas??"

inwit -

Genial!! Muchas gracias, tio Petros! :-)