El Teorema de Wallace-Simson
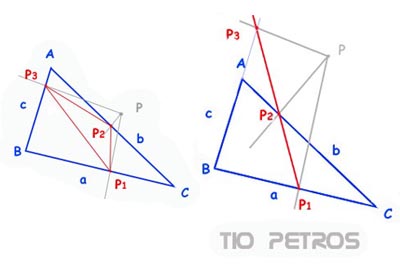
Seguimos con nuestro paseo por los hermosísimos parajes de la geometría plana de los triángulos.Supongamos que tenemos un triángulo cualquiera, definido por sus vértices A,B,C como en la figura(triángulos azules). Dado un punto cualquiera P (en gris en las figuras), que puede ser exterior o interior al triángulo, tracemos las tres perpendiculares desde dicho punto hasta los tres lados del triángulo, o hasta sus prolongaciones en su caso.
Los puntos P1,P2,P3 de intersección determinan un triángulo que denominaremos Triángulo podal del triángulo ABC relativo al punto P. Lo tenemos en rojo en las figuras.
Resulta que este triángulo degenera en un segmento en determinados casos. En la figura de la derecha podemos ver que para el punto P elegido, los puntos P1,P2,P3 están alineados, con lo que el triángulo podal es un segmento.
Cuando esto ocurre, la recta definida por los tres puntos alineados se denomina Recta de Wallace-Simpson del triángulo dado respecto al punto P
El Teorema de Wallace-Simson afirma que :
El lugar geométrico de todos los puntos P para los cuales los tres puntos antes citados están alineados es precisamente la circunferencia circunstrita del triángulo original.
Según el punto P va recorriendo la circunferencia circunscrita al triángulo original, la recta de Wallace-Simpson correspondiente va girando.
El Teorema de Steiner afirma que la envolvente de todas las rectas de Wallace.Simpson de un triángulo dado es una deltoide tricúspide .
Aquí tienen ustedes una generalización del teorema de Wallace-Simson debido a Don Miguel de Guzmán, recientemente fallecido como hemos comentado hace unos días. Dicha generalización consiste en no limitar la dirección de las rectas desde el punto P hasta los lados del triángulo.
El propio Miguel de Guzmán recuerda su encuentro con el teorema de Steiner tras trabajar con la envolvente de todas las rectas de Wallace-Simson de un triángulo dado.
En la imagen tienen la deltoide tricúspide de Steiner como envolvente de una familia de rectas de Wallace-Simson.
Por cierto: Una vez más parece que la historia no ha sido justa. Simson parece no tener nada que ver con el teorema citado, que es obra exclusiva de Wallace. Ambos eran matemáticos escoceses, y Wallace logró su demostración en 1856.
En esta dirección el profesor Guzmán nos propone una demostración "sencilla" del teorema de la deltoide de Steiner, demostración lograda por él mismo.
10 comentarios
RAFAEL MENESES CUADROS -
En arcos iguales el ángulo de intersección de líneas
Secantes es igual al ángulo de deflexión, y el eje X en
Giro tangencial forma la bisectriz de las líneas
Secantes
TEOREMA APLICADO EN METODO DE LA SECANTE PARA CONSTRUCCION
DE CURVAS EN MINERIA SUBTERRANEA
raul -
leolo -
En cuanto a comentarios absurdos... mejor no comentarlos.
maite -
Anónimo -
alejandra aceveda -
cieñito -
Laura -
Por cierto el artículo me parece por demás interesante
ad -
maico -