Blogia
Tio Petros

El teorema de Napoleón Bonaparte

- Teoremas
El teorema de Napoleón Bonaparte No deja de ser curioso que un tema tan manido, tan antiguo y tan básico y elemental como la geometría de los triángulos planos tenga tantas sorpresas.

Hace unos meses comentábamos el teorema de Morley, bello teorema que concierne a triángulos y que fué demostrado anteayer, como quien dice(en pleno siglo XX).

El teorema que comentamos hoy tiene como curioso, además de su contenido matemático, la atribución de paternidad: nada menos que al gran Napoleón Bonaparte.

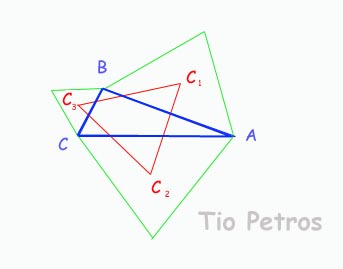
Supongamos un triángulo general cualquiera (dibujado en azul). Sobre cada uno de sus lados dibujamos un triángulo equilátero (dibujado en verde). Pues bien: los centros de los trres triángulos equiláteros forman a su vez un triángulo necesariamente equilátero (dibujado en rojo), con independencia del triángulo original.

Este es el denominado Teorema de Napoleón .

En esta dirección podéis ver la demostración, así como los conceptos previos necesarios para entenderla.

Respecto a la paternidad de la demostración, parece fuera de toda duda que no es de Bonaparte, sino de Lorenzo Mascheroni , quien sabiendo la pasión del general francés por la geometría, dedicó su libro Geometria del Compasso (Pavia, Pietro Galeazzi, anno V della Republica Francese, 1797) a Napoleon:

Según podemos leer en esta dirección,

El aprecio de Napoleón por la obra de Mascheroni fue grande y la hizo traducir al francés: Mascheroni Lorenzo: _Geometrie du compas_, Ouvrage traduit de l'italien par

A.M. Carette, Paris, Duprat, xxiv, 263 pp. 14 plates, 1798.


En todo caso, si por la relación entre uno y otro, el general se llevó a la posteridad el nombre del teorema de forma injusta, Mascheroni se desquitó uniéndo su nombre al del gran Euler en la que hoy en día se conoce como la constante de Euler-Mascheroni , denominación injusta según explica estupendamente Mario Bunge en su artículo publicado en el rincón matemático.

Y es que el tema de las atribuciones y los honores en los logros científicos es un tema bastante escabroso en general, tanto o más que el tema de las atribuciones de inventos. Ya hablaremos de ello en otra ocasión...


ADICION POSTERIOR:

Me escribe Mario Bunge para decirme que:

Por favor, corregí lo que pusiste sobre Mascheroni: No soy yo quien lo explica "estupendamente", porque el artículo ese no es mío: es de William Dunham. Lo único que hice yo fue tipear texto y ecuaciones, y hacer los dibujitos con el "dibujador" del Word. Todo lo demás es obra de Dunham.

Pues dicho queda. No obstante, no quería dejar pasar la oportunidad para comentar que el rincón matemático es una página de interés enorme para todo amante de la matemática.

16 comentarios

Jordan 11 -

Time cures sorrows and squabbles because we all change, and are no longer the same persons. Neither the offender nor the offended is the same.

napoleon -

me gustaria saber como es que napoleon aplicaba lo del triangulo de napoleon , o como es que lo invento, porque, con que fin

Fabián -

Estoy trabajando con un alumno en la resolución de problemas geométricos básicos empleando únicamente regla de bordes paralelos. ¿Existe alguna bibliografía al respecto?
Gracias

Anónimo -

esta malisima la pagina

evelin -

me parecio un poco interesante

goloso -

muy bonito el teorema me gustaria saber que aplicaciones tiene

tonny -

hace tiempo que busco la demostracion del teorema de soddy tal vez pudieran publicarla.Gracias .

KAREN -

cual es el teorema de los triangulos

jose luis garcia -

tienen q poner la demostracion de soddy

lauri -

aburrido

Anónimo -

cual es el teorema de los triangulos

Jhonathan -

Edgar L. Ruiz -

me gustaria que presentaran la demostracion del teorema de Napoleon en la pagina o que si son tan amables que me la mandaran. Gracias

Anita de Argentina -

necesito datos de la demostración de la bisección de un arco sólo con compás. Gracias!!!!!

Tio Petros -

Lo tiene, lo tiene. A mi también me lo parece. En general toda la geometría plana, por aquello de la regla y el compás tiene reminiscencias algo masónicas y mistéricas. Forma parte del encanto...

dob -

La estrella, la "magia" de los números y las proporciones... ¿Tiene un aire cabalístico este teorema de los triángulos, o a mí me lo parece?
¿Era masón Napoleón?