El teorema de Pick (2)
Para que no haya confusión es importante explicar que cuando en este post nos refiramos a los puntos de la frontera o del interior de un polígono cualquiera nos estaremos refiriendo exclusivamente a los puntos de la malla de Pick de dichos polígonos.Vamos a demostrar que la función V(P) = I+ B/2 1 definida sobre polígonos de Pick explicada en el post anterior es una función aditiva. Esto es: si el polígono P resulta de la unión de los polígonos P1 y P2, entonces :
V(P)=v(P1)+v(P2)
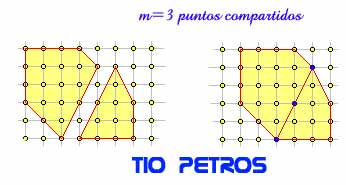
Sean pues dos polígonos de Pick P1 y P2, con I1 e I2 puntos de la cuadrícula en el interior de los mismos; y con B1 y B2 puntos de la cuadrícula en su frontera respectivamente. Llamaremos m al número de puntos del polígonos resultante P que provienen de la coincidencia de dos puntos de la frontera de ambos polígonos iniciales. Está claro que dichos puntos serán puntos internos de P salvo los dos extremos, que seguirán perteneciendo a la frontera.
Así pues, podemos pasar a comprobar que V(P) es precisamente la suma de V(P1) y V(P2).
Tenemos:
V(P1) = I1 + B1/2 1
V(P2) = I2 + B2/2 1
V(P) = I + B/2 1.
El número de puntos internos de P será la suma de los de los polígonos iniciales P1 y P2 más la cantidad de puntos frontera de éstos que se han convertido en interiores. Dicha cantidad es de (m-2), pues los dos puntos extremos de los m que coinciden siguen siendo frontera en el polígono resultante, convirtiéndose en interiores los demás. Así pues tenemos que:
I = I1 + I2 + m 2.
Respecto a los puntos de la frontera de P vemos que provienen de los puntos frontera originales, excepto precisamente los m compartidos, que pasan a ser internos todos ellos menos los dos extremos. Así pues:
B= B1 + B2 - 2m + 2
Ahora estamos en condiciones de afrontar la prueba de aditividad:
V(P) = I + B/2 1 = (I1 + I2 + m 2) + (B1 + B2 - 2m + 2)/2 1 =
= (I1 + B1/2 1 ) + (I2 + B2/2 1) = V(P1) +
V(P2), que es lo que queríamos demostrar.
Queda demostrada la aditividad de la medida propuesta. Esto no sólo es importante por ser condición necesaria para que dicha medida sea efectivamente un área, sino porque además nos habilitará para demostrar que para figuras sencillas como triángulos efectivamente ES un área. Dado que cualquier polígono de Pick puede triangularse, aplicando la aditividad quedará demostrado que la fórmula es válida para todos ellos.
La doble arma de poder demostrar lo que queremos para figuras muy sencillas de forma directa y aplicar luego aditividad para extender la veracidad de la afirmación a figuras más complicadas nos habilitará para comprender una interpretación nada evidente de la fórmula de Pick: los ángulos de visión del polígono dado desde cada uno de los puntos de la malla.
Efectivamente, vean la siguiente ilustración:
Vamos a efectuar el conteo de los ángulos de visión del polígono desde cada uno de los puntos del mismo. La unidad del conteo será la circunferencia completa. Comprenderán que un punto interior como el i de la figura contabiliza como una unidad: su "angulo de visión del polígono" es la circunferencia entera por pertenecer al interior del polígono. Un punto como b , contabilizará como media unidad, pues pertenece a la frontera sin ser un vértice, y tiene un ángulo de visión del polígono de media circunferencia. Si el polígono es un triángulo, los ángulos de visión de los vértices son precisamente los propios ángulos de los vértices, que suman siempre media circunferencia (180º), lo que hace media unidad entre los tres. O lo que es lo mismo: podemos contabilizar dichos vértices como cualquier punto de la frontera y luego restar una unidad al resultado, obteniendo la fórmula original de Pick: I+B/2 -1.
Dado que lo anterior es válido para cualquier triángulo y daddo que cualquier polígono de Pick se puede triangular, basta ver la aditividad de esta "nueva forma de ver las cosas", pero esto ahora es casi trivial: si tenemos dos polígonos que se unen, sus puntos respectivos siguen contabilizando como en los originales salvo cuando pertenecen a la frontera. Si dicha parte de la frontera no es de la zona de unión, nada ocurre. Si lo es pueden pasar dos cosas: que el punto pase a ser interior o que continúe siendo frontera del polígono suma.
Si sucede lo primero, dos puntos frontera que tenían un ángulo de visión de media circunferencia cada uno pasan a ser un punto interior con un ángulo de una circunferencia completa y se conserva la aditividad. Si sucede lo segundo, dos vértices se unen en un punto que sigue siendo un vértice, pero en este caso también se suman los ángulos de visibilidad, luego también se conserva la aditividad.
En suma: el sumatorio de los ángulos de visibilidad de todos los puntos de la malla de Pick de un polígono dado nos da el área de dicho polígono, medidos dichos ángulos en circunferencias completas.
¿No es curioso?
En el próximo post veremos que el teorema de Pick es más potente de lo que parece: todo lo aquí dicho valía para polígonos de Pick convexos o no convexos, pero sin agujeros. Una pequeña ampliación en el mismo lo habilita para todo tipo de polígonos de Pick, incluso con agujeros.
7 comentarios
Sildenafil -
JOAB ISAI MUÑOZ GONZALEZ -
mewt -
Descomposicion de un poligono de Pick en componentes simplemente conexas o algo como Area = Area sin agujeros - Area agujeros ?
Lo espero con impaciencia...
PS: Gracias por el link al post de los mosaicos en el plano, las fotos de la Alhambra me hacen sentir como en casa :-D
JuanPablo -
chuchi -
gustaria insistencia en ideas
de fudamento dificiles de comprender, y que tú sabes enfocar con maestria como:
Lo continuo
Lo medible
Lo numerable
Lo convergente
Lo equivalente
Lo generable
Y por último abusando de tu amabilidad, un temita, sobre
estructura, morfismo, e isomorfia.
Thanks.
Antón -
Matías -
No vale. Matemático tenía que ser ;)