El teorema de Pick (2)
 Para que no haya confusión es importante explicar que cuando en este post nos refiramos a los puntos de la frontera o del interior de un polígono cualquiera nos estaremos refiriendo exclusivamente a los puntos de la malla de Pick de dichos polígonos.
Para que no haya confusión es importante explicar que cuando en este post nos refiramos a los puntos de la frontera o del interior de un polígono cualquiera nos estaremos refiriendo exclusivamente a los puntos de la malla de Pick de dichos polígonos.Vamos a demostrar que la función V(P) = I+ B/2 1 definida sobre polígonos de Pick explicada en el post anterior es una función aditiva. Esto es: si el polígono P resulta de la unión de los polígonos P1 y P2, entonces :
V(P)=v(P1)+v(P2)
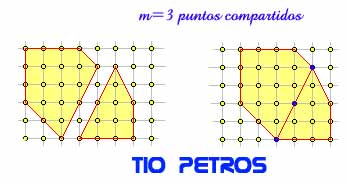
Sean pues dos polígonos de Pick P1 y P2, con I1 e I2 puntos de la cuadrícula en el interior de los mismos; y con B1 y B2 puntos de la cuadrícula en su frontera respectivamente. Llamaremos m al número de puntos del polígonos resultante P que provienen de la coincidencia de dos puntos de la frontera de ambos polígonos iniciales. Está claro que dichos puntos serán puntos internos de P salvo los dos extremos, que seguirán perteneciendo a la frontera.
Así pues, podemos pasar a comprobar que V(P) es precisamente la suma de V(P1) y V(P2).
Tenemos:
V(P1) = I1 + B1/2 1
V(P2) = I2 + B2/2 1
V(P) = I + B/2 1.
El número de puntos internos de P será la suma de los de los polígonos iniciales P1 y P2 más la cantidad de puntos frontera de éstos que se han convertido en interiores. Dicha cantidad es de (m-2), pues los dos puntos extremos de los m que coinciden siguen siendo frontera en el polígono resultante, convirtiéndose en interiores los demás. Así pues tenemos que:
I = I1 + I2 + m 2.
Respecto a los puntos de la frontera de P vemos que provienen de los puntos frontera originales, excepto precisamente los m compartidos, que pasan a ser internos todos ellos menos los dos extremos. Así pues:
B= B1 + B2 - 2m + 2
Ahora estamos en condiciones de afrontar la prueba de aditividad:
V(P) = I + B/2 1 = (I1 + I2 + m 2) + (B1 + B2 - 2m + 2)/2 1 =
= (I1 + B1/2 1 ) + (I2 + B2/2 1) = V(P1) +
V(P2), que es lo que queríamos demostrar.
Queda demostrada la aditividad de la medida propuesta. Esto no sólo es importante por ser condición necesaria para que dicha medida sea efectivamente un área, sino porque además nos habilitará para demostrar que para figuras sencillas como triángulos efectivamente ES un área. Dado que cualquier polígono de Pick puede triangularse, aplicando la aditividad quedará demostrado que la fórmula es válida para todos ellos.
La doble arma de poder demostrar lo que queremos para figuras muy sencillas de forma directa y aplicar luego aditividad para extender la veracidad de la afirmación a figuras más complicadas nos habilitará para comprender una interpretación nada evidente de la fórmula de Pick: los ángulos de visión del polígono dado desde cada uno de los puntos de la malla.
Efectivamente, vean la siguiente ilustración:

Vamos a efectuar el conteo de los ángulos de visión del polígono desde cada uno de los puntos del mismo. La unidad del conteo será la circunferencia completa. Comprenderán que un punto interior como el i de la figura contabiliza como una unidad: su "angulo de visión del polígono" es la circunferencia entera por pertenecer al interior del polígono. Un punto como b , contabilizará como media unidad, pues pertenece a la frontera sin ser un vértice, y tiene un ángulo de visión del polígono de media circunferencia. Si el polígono es un triángulo, los ángulos de visión de los vértices son precisamente los propios ángulos de los vértices, que suman siempre media circunferencia (180º), lo que hace media unidad entre los tres. O lo que es lo mismo: podemos contabilizar dichos vértices como cualquier punto de la frontera y luego restar una unidad al resultado, obteniendo la fórmula original de Pick: I+B/2 -1.
Dado que lo anterior es válido para cualquier triángulo y daddo que cualquier polígono de Pick se puede triangular, basta ver la aditividad de esta "nueva forma de ver las cosas", pero esto ahora es casi trivial: si tenemos dos polígonos que se unen, sus puntos respectivos siguen contabilizando como en los originales salvo cuando pertenecen a la frontera. Si dicha parte de la frontera no es de la zona de unión, nada ocurre. Si lo es pueden pasar dos cosas: que el punto pase a ser interior o que continúe siendo frontera del polígono suma.
Si sucede lo primero, dos puntos frontera que tenían un ángulo de visión de media circunferencia cada uno pasan a ser un punto interior con un ángulo de una circunferencia completa y se conserva la aditividad. Si sucede lo segundo, dos vértices se unen en un punto que sigue siendo un vértice, pero en este caso también se suman los ángulos de visibilidad, luego también se conserva la aditividad.
En suma: el sumatorio de los ángulos de visibilidad de todos los puntos de la malla de Pick de un polígono dado nos da el área de dicho polígono, medidos dichos ángulos en circunferencias completas.
¿No es curioso?
En el próximo post veremos que el teorema de Pick es más potente de lo que parece: todo lo aquí dicho valía para polígonos de Pick convexos o no convexos, pero sin agujeros. Una pequeña ampliación en el mismo lo habilita para todo tipo de polígonos de Pick, incluso con agujeros.







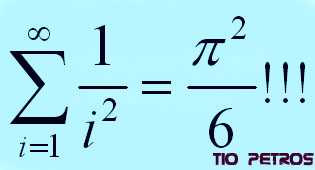 Las admiraciones de la fórmula que encabeza este post no son factoriales: son simples exclamaciones que reflejan la sorpresa que produjo en el mundo matemático el descubrimiento de Euler.
Las admiraciones de la fórmula que encabeza este post no son factoriales: son simples exclamaciones que reflejan la sorpresa que produjo en el mundo matemático el descubrimiento de Euler.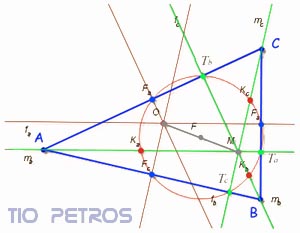 El Teorema de Feuerbach ha sido denominado como la joya de la geometría del siglo XIX . Y realmente no es para menos... Les invito a acercarse un poco al sabor de dicho teorema; como siempre, sin demostraciones y sin hacer matemáticas; tan solo paseando agradablemente.
El Teorema de Feuerbach ha sido denominado como la joya de la geometría del siglo XIX . Y realmente no es para menos... Les invito a acercarse un poco al sabor de dicho teorema; como siempre, sin demostraciones y sin hacer matemáticas; tan solo paseando agradablemente.
 Seguimos con nuestro paseo por los hermosísimos parajes de la geometría plana de los triángulos.
Seguimos con nuestro paseo por los hermosísimos parajes de la geometría plana de los triángulos.
 No deja de ser curioso que un tema tan manido, tan antiguo y tan básico y elemental como la geometría de los triángulos planos tenga tantas sorpresas.
No deja de ser curioso que un tema tan manido, tan antiguo y tan básico y elemental como la geometría de los triángulos planos tenga tantas sorpresas. A diferencia de la mayoría de los post de este blog, este, y quizás los que sigan exige un poco más de esfuerzo para su comprensión. No obstante, creo que vale la pena. Vamos a intentar entender un teorema difícil. Eso nunca NUNCA es gratis. Además, vamos a intentarlo sin utilizar matemáticas, o casi. Esta vez, el paseo que les propongo es más escarpado. Pero coincidirán conmigo en que el placer de alcanzar la cumbre es proporcional a la pendiente dejada a nuestras espaldas.
A diferencia de la mayoría de los post de este blog, este, y quizás los que sigan exige un poco más de esfuerzo para su comprensión. No obstante, creo que vale la pena. Vamos a intentar entender un teorema difícil. Eso nunca NUNCA es gratis. Además, vamos a intentarlo sin utilizar matemáticas, o casi. Esta vez, el paseo que les propongo es más escarpado. Pero coincidirán conmigo en que el placer de alcanzar la cumbre es proporcional a la pendiente dejada a nuestras espaldas.  Hemos hablado varias veces sobre el Teorema de los cuatro colores.Decíamos que era un ejemplo clásico de dificultad de demostración matemática, aunque el enunciado era entendible por todo el mundo:
Hemos hablado varias veces sobre el Teorema de los cuatro colores.Decíamos que era un ejemplo clásico de dificultad de demostración matemática, aunque el enunciado era entendible por todo el mundo: 

 Existe una tendencia en biología a considerar que dada una característica fenotípica (visible, corporal), hay un motivo genotípico que la causa.Se razona que si existe tal cosa es porque ha habido una ventaja selectiva para los poseedores de tal característica. Pondré un ejemplo: se encuentra un fósil de un reptil volador, el nyctosaurus ; como el relatado
Existe una tendencia en biología a considerar que dada una característica fenotípica (visible, corporal), hay un motivo genotípico que la causa.Se razona que si existe tal cosa es porque ha habido una ventaja selectiva para los poseedores de tal característica. Pondré un ejemplo: se encuentra un fósil de un reptil volador, el nyctosaurus ; como el relatado  Un mosaico es una composición con losetas que reproduce un paisaje o una figura. Cuando las losetas llenan el plano basándose en simetrías, desplazamientos y rotaciones, estamos ante un mosaico geométrico. De estos últimos vamos a hablar ahora.
Un mosaico es una composición con losetas que reproduce un paisaje o una figura. Cuando las losetas llenan el plano basándose en simetrías, desplazamientos y rotaciones, estamos ante un mosaico geométrico. De estos últimos vamos a hablar ahora. ______
______ ______
______
 ________
________ La matemática es infinita, a diferencia del mundo real. Nunca acabaremos de descubrir todos los secretos del humilde conjunto N de números naturales, por ejemplo, dado que es infinito el número de sus enigmas. Cualquier rama de la matemática plantea infinitos enigmas, y nunca tendremos tiempo de desvelarlos todos.Por eso no debe sorprendernos que ciertos bellos teoremas que conciernen a humildes triángulos planos no hayan sido descubiertos hasta el siglo XX.
La matemática es infinita, a diferencia del mundo real. Nunca acabaremos de descubrir todos los secretos del humilde conjunto N de números naturales, por ejemplo, dado que es infinito el número de sus enigmas. Cualquier rama de la matemática plantea infinitos enigmas, y nunca tendremos tiempo de desvelarlos todos.Por eso no debe sorprendernos que ciertos bellos teoremas que conciernen a humildes triángulos planos no hayan sido descubiertos hasta el siglo XX. Un teorema es una frase que afirma algo, seguida de la demostración. Este teorema es extraordinario, único diría yo, por tres motivos: Primero: el enunciado es tan simple que lo entiende cualquiera, independientemente de su formación. Segundo: la afirmación que hace parece tan obvia que todo el mundo se asombra de que eso sea un teorema que necesite demostración. Tercero: la demostración es endiabladamente difícil. Si se hace por métodos elementales es larguísima y tediosa en extremo; se puede hacer una demostración mucho más corta, pero para ello hay que invocar conocimientos muy sofisticados de topología, que es una rama de la matemática de lo que hablaremos otro día.
Un teorema es una frase que afirma algo, seguida de la demostración. Este teorema es extraordinario, único diría yo, por tres motivos: Primero: el enunciado es tan simple que lo entiende cualquiera, independientemente de su formación. Segundo: la afirmación que hace parece tan obvia que todo el mundo se asombra de que eso sea un teorema que necesite demostración. Tercero: la demostración es endiabladamente difícil. Si se hace por métodos elementales es larguísima y tediosa en extremo; se puede hacer una demostración mucho más corta, pero para ello hay que invocar conocimientos muy sofisticados de topología, que es una rama de la matemática de lo que hablaremos otro día.