Blogia
Tio Petros

Una joyita: el Teorema de Morley

- Teoremas
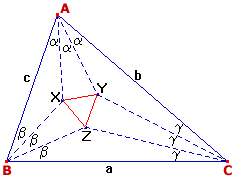
Una joyita: el Teorema de Morley La matemática es infinita, a diferencia del mundo real. Nunca acabaremos de descubrir todos los secretos del humilde conjunto N de números naturales, por ejemplo, dado que es infinito el número de sus enigmas. Cualquier rama de la matemática plantea infinitos enigmas, y nunca tendremos tiempo de desvelarlos todos.Por eso no debe sorprendernos que ciertos bellos teoremas que conciernen a humildes triángulos planos no hayan sido descubiertos hasta el siglo XX.

Sabemos desde antiguo que si en cualquier triángulo trazamos las bisectrices (rectas que dividen cada ángulo en dos partes iguales)de sus tres ángulos, las tres se cortan en un mismo punto, que denominamos incentro del triángulo. Ahora bien: ¿qué sucede si en vez de bisectrices trazamos por cada ángulo las dos rectas que lo dividen en tres ángulos iguales?

Pues lo que ocurre es lo que nos dice el Teorema de Morley :

Los puntos de intersección de las rectas que dividen en tres partes iguales los ángulos de cualquier triángulo son los vértices de un triángulo equilátero.

Efectivamente, sin importar cómo es el triángulo inicial, el triángulo interno resultante de unir los puntos de intersección de las "trisectrices" adyacentes es un perfecto, increíble y sorprendente triángulo equilátero.
Frank Morley (1860-1937) encontró en 1904 la demostración de bello teorema que hemos reproducido aquí, y que lleva su nombre.

La demostración completa del teorema, por si alguien quiere seguirla está aquí.

14 comentarios

Tadalafil -

Este teorema me dio muchos dolores de cabeza en la universidad, para mi es muy complicado de entender.

diego -

hay otras demostraciones, personalmente me gusta la de A. ROBSON. es cencilla, pero la de morley es monstruosa.
con respecto a la pregunta si es posible construir las trisectices no es posible la construccion con regla y compaz, pero si por otros metodos. o sobre la demostracion sobre el resiproco, solo estarias dando casos particulares, ademas de que el teorema es una implicancia, personalmente no creo que resulte

diego -

es un teorema impresionante, tantos años dentro de una geometria que delante de nuestros ojaos salgan cosas como esta, peo quisiera responder algunas preguntas.

AnDrEa -

hay alguna otra forma de demostrar ese teorema?...más sencilla..?

Paola -

¿Cuáles son las aplicaciones del teorema de Morley?

jchl -

todo esta en el estado mentalporque muchas carreras se han perdido antes de haberlas corrido piensa en grande y tus hechos creceran todo esta en el estado mental "mas importante es la imaginacion que el conocimiento)..........albert einstein

jchl -

partiendo del reciproco costruyan el equilatero y llegen a demostrar que son trisecados los angulos , seria otra forma ingeniosa

Miguel Arroyo(alumno) -

¿Existira otro metodo mas sencillo de poder demostrar el teorema de Morley?

eieoeoeoe -

ytrytryhgdfgfdgfgfg

Rita Cantero -

¿Es posible construir las trisectrices de cualquier triángulo?

Javier -

Pilar, el punto X es la intersección de las dos trisectrices adyacentes que parten de A y B respectivamente.

Para contruir un triángulo con los ángulos trisecados, lo único que puedes hacer es partir de tres ángulos que sumen 60º, triplicarlos y obtendrás tres ángulos que suman 180º, con los cuales puedes construir un triángulo.

Pilar -

La primera linea de la demostracion dice:
"Aplicando el teorema del seno al triángulo BXA resulta "

¿como se elige el punto X en el interior del triangulo? ¿es un punto cualquiera? ¿COmo se construyen estas "trisectrices"? es bien sabido que , en general, no es posible encontrarlas, no?

Anónimo -

Yusent -

En lo personal me parecio una demostracion muy buena, ya que me gusta mucho la trigonometria, ademas ese teorema no lo conocia. Aun asi creo que pudieron interpretar la solucion de una manera mas simple.