Clasificando puntos
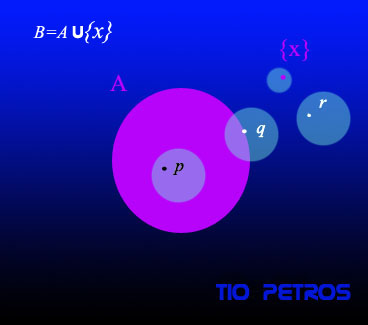
Ha llegado el momento de ver la aplicación práctica de todo lo que hemos visto hasta ahora. Consideremos la topología usual en el plano. Los abiertos de la misma son uniones arbitrarias de bolas abiertas , que no son sino el conjunto de los puntos que están a una distancia menor que un valor dado de otro punto que es su centro. Cuando una topología es de este tipo, con una base formada a partir de la definición de una distancia es que previamente estamos en un espacio métrico, y la topología se denomina topología métrica asociada a la distancia. Si, como en este caso, la distancia definida es la habitual, euclídea, podemos hablar de topología euclídea .Pues bien, vamos a ver que la mera consideración de un subconjunto de un espacio topológico establece una clasificación de los puntos del espacio, clasificación más rica que la que teníamos hasta ahora, y que se resumía en hablar de qué puntos pertenecían o no a qué conjunto. El conjunto a considerar es el de la figura: Un círculo A y un punto exterior al mismo, {x}. Consideraremos el objeto B= A U {x} resultante de la unión de ambos.
Sea B el subconjunto de un conjunto X dotado de una topología T ( Dicho de otra forma: sea B un subconjunto en un espacio topológico (X,T).
Definimos:
Punto interior de B es todo punto p para el cual existe un abierto que contenga a p y esté totalmente contenido en B. Al conjunto de todos los puntos interiores de B lo llamaremos interior de B en un alarde de imaginación, y lo denotaremos así: int(B).
Punto exterior de B es todo punto r para el cual existe un abierto que contenga a p y esté totalmente contenido en el complementario de B. Al conjunto de todos los puntos exteriores de B lo llamaremos exterior de B , y lo denotaremos así: ext(B).
Punto frontera es todo punto q para el cual, cualquier entorno del mismo corta (tiene intersección no vacía) tanto a B como a su complementario. Al conjunto de todos los puntos frontera de B lo llamaremos frontera de B , y lo denotaremos así: fr(B).
Cualquier punto del espacio completo es de una de estas tres categorías, pues las tres forman un conjunto exhaustivo de posibilidades, luego el espacio completo se divide en tres partes al considerar cualquier subconjunto:
X= int(B) U ext (B) U fr (B), para todo subconjunto B de X.
Hay que hacer notar que un punto interior pertenece al subconjunto, y un punto exterior pertenece a su complementario. Sin embargo, un punto frontera puede pertenecer o no al mismo.
Parecería que esta clasificación es satisfactoria completamente, pero la cosa dista mucho de ser así. El conjunto B considerado tiene por definición un punto x fuera del círculo A, y por lo tanto x B. Sin embargo, no hay entorno alguno de x incluido en B, ni incluido en su complementario pues el propio x pertenece a B. Así pues, ni pertenece al interior ni al exterior de B. Por lo tanto pertenece a la frontera de B.
Sin embargo, algo nos dice que su estatus es diferente a la de los puntos de la circunferencia que delimita el círculo A.
Se trata de un punto aislado, que nos muestra que debemos ser más finos en nuestra clasificación. En el próximo post hablaremos de los trascendentales conceptos de adherencia y acumulación, y tendremos una visión más rica del asunto.
Hasta entonces, si algún lector se encuentra con esto por vez primera y lo comprende; un ejercicio interesante es encontrar el interior, exterior y frontera de subconjuntos algo más diabólicos que el representado. Si se animan, piensen en hacerlo con el subconjunto Q de los racionales dentro de la recta R de los reales, también con la topología euclídea usual. Es un ejercicio interesante y no trivial.
Hasta el próximo post.
5 comentarios
Sildenafil -
A -
Hugolinox -
Toda ayuda se agradece chaus
José María -
Muchísimas gracias por tus exposiciones :D
Cluje -