Integral de Lebesgue de funciones simples
Viene de aquí.
Según hemos visto aquí existe una definición muy clara de le integral de Lebesgue para las funciones simples. Tanto que parece muy poca cosa después de tanta introducción. Sin embargo, es notable el hecho de que tan poca cosa consigue vencer a la indomable función de Dirichlet.
Repetiremos aquí que la idea de Lebesgue es dividir el dominio de integración en particiones relativas a los valores de la propia función. En las siguientes ilustraciones veremos una vez más la diferencia entre la integral de Riemann y la de Lebesgue para una función simple general
Sea la función simple:
f= 2 · I(0,1]U(6,8] + 3 · I(1,6)]
Espero que la nomenclatura esté clara: la función vale 2 para los puntos del conjunto (0,1]U(6,8] y vale tres para los del conjunto (1,6] , valiendo cero en el resto.
La tenemos aquí:
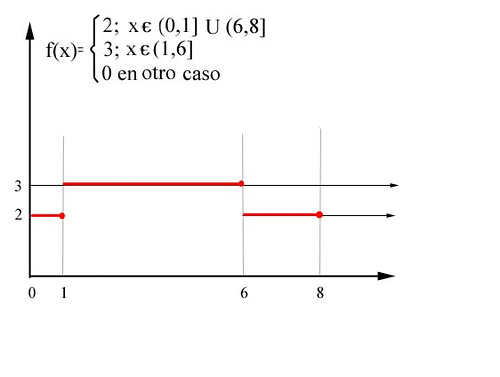
La integración de Riemann dividirá el intervalo de intergración en rectángulos cada ver más finos, evaluando el área de cada uno, de la siguiente forma:
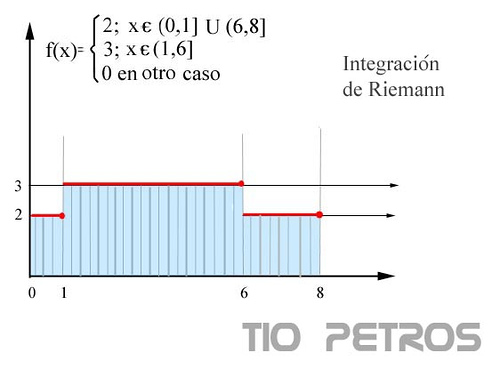
La integraciónde Legesgue, en cambio dividirá el intervalo de integración en sólo dos partes, una para los puntos en los que la función vale 2 y otra para los puntos en los que la función vale 3, sumando los productos de las medidas respectivas de los dos trozos por 2 y por 3 respectivamente:
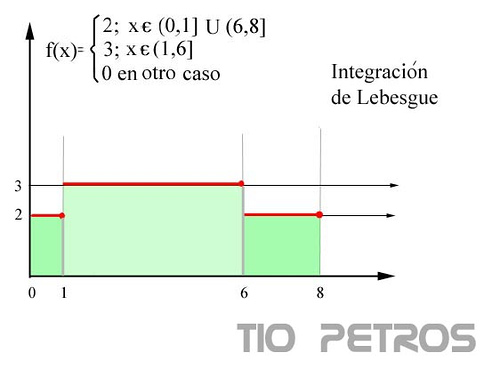
Es obvio que en ambos casos la integral va a a valer 21: el área bajo la función.
En el caso de la función de Dirichlet (circunscrita al intervalo [0,1], por muy complicada que nos pareciera desde el punto de vista de la continuidad o de cualquier propiedad topológica, a la luz de "lo que verdaderamente importa" para Lebesgue, es una función muy sencilla: es una función simple. Más aún: es una sencilla función indicatriz que toma valor uno para los puntos irracionales y valor cero para los racionales.
Así pues, la integral valdrá:
I=1·m(R-Q) + 0.m(Q)
Dado que el conjunto de los racionales del intervalo [0,1] tiene medida cero, el conjunto de los irracionales del mismo intervalo tendrá medida uno, y la integral valdrá I = 1·1+0·0 = 1. El valor de la integral es el mismo que para la función unidad, de lo que se deduce que para la integración de Lebesgue, todo conjunto de medida nula no aporta absolutamente nada al valor de la integral. Esto es una simplificación extraordinaria, porque de un plumazo evitamos todos los comportamientos patológicos de funciones extrañas cuyas irregularidades no nos hacen más que molestar.
Aunque esto parece cosa de niños, las buenísimas propiedades en el límite de esta integral así definida nos habilitarán extrapolarla sin demasiados problemas a toda función medible. Entonces comprenderemos la potencia de la nueva herramienta, y lo que más nos importa: el porqué de la misma. Lo haremos lentamente porque no tenemos prisa.
8 comentarios
Vicente -
ronald -
Danys Orozco -
Dani -
Jose Brox -
jose -
TioPetros -
Gracias.
Dr. Jekyll -