Cardinalidad, "tamaño", medida, dimensión (2)
Vamos a dedicar este post a la nada desdeñable tarea de demostrar que un subconjunto dey intervalo de la recta [0,1] puede tener medida de Lebesgue igual a ceo, a pesar de tener la misma cardinalidad que el intervalo completo [0,1].Lo haremos de la forma más expeditiva posible: mostrando un conjunto concreto que tenga dichas propiedades. Puede resultar chocante, pero nada de lo que aquí se va a decir es nuevo: todo está muy claro y aceptado desde hace más de un siglo. Pero sirve para comprender que la relación entre cardinalidad y medida es tortuosa: podemos afirmar que un conjunto de cardinalidad numerable tiene medida cero, pero no podemos afirmar que tenga medida mayor que cero por el hecho de tener cardinalidad infinita no numerable.
El conjunto en cuestión, como ya avanzamos hace dos posts, es el conjunto de Cantor .
Se forma a partir del intervalo [0,1], y es el conjunto límite de un proceso infinito que consiste en dividir el cada intervalo del conjunto anterior en tres partes iguales y eliminar la central.
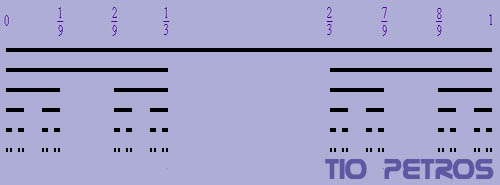
Como podemos ver en la figura, partiendo del intervalo C0 = [0,1] tenemos la división [0,1/3]; [1/3,2/3]; [2/3,1]. Eliminando la central, tenemos el conjunto C1 = [0,1/3] U [2/3,1].
Este nuevo conjunto está formado por dos intervalos, que divididos en tres partes y eliminada la central, dará paso a C2; y así sucesivamente.
Pues bien, el conjunto de Cantor es el límite del proceso, y lo llamaremos C .
Nuestra tarea, ahora que está perfectamente definido el objeto es doble: demostrar que tiene la cardinalidad del original [0,1], y demostrar que tiene medida cero.
Comenzaremos por lo segundo.
DEMOSTRACIÓN DE MEDIDA NULA DEL CONJUNTO DE CANTOR
Esta demostración es una tontería al alcance de cualquiera que sepa sumar series geométricas. Dado que los trozos que vamos quitando en las sucesivas etapas son disjuntos (obviamente), podemos sumar la medida total que sustraemos (llamémosla A) simplemente sumando las medidas individuales de los trocitos que vamos quitando en cada etapa, por la aditividad de la medida de Lebesgue.
En la primera etapa quitamos un trozo que mide 1/3, en la segundo dos trozos que miden 1/9 cada uno, y así sucesivamente. El desarrollo completo lo tenemos aquí:
Vemos que la medida sustraída es la unidad, luego invocando una vez más la aditividad, la medida del conjunto de Cantor es exactamente cero.
Para deducir la cardinalidad del mismo he encontrado en la web una demostración impecable, que explico a continuación:
DEMOSTRACIÓN DE CARDINALIDAD INFINITO NO NUMERABLE
Verificaremos la existencia de una biyección entre los puntos del conjunto de Cantor y el intervalo [0,1].
Para ello, expresaremos los puntos en base tres. La expresión decimal en base 3 de un número del intervalo [0,1] será de la forma 0,0XXXX... cuando pertenece al primer tercio del intervalo; 0,1XXX... cuando pertenece al segundo y 0,2XXX cuando pertenece al tercero. Eliminar el tercio central en la primera etapa es simplemente eliminar todos los puntos que tienen un 1 en su primer decimal.
De la misma manera, el segundo decimal será 0,1 ó 2 si el número (o punto ) correspondiente pertenece al primer tercio, segundo o tercero de cualquiera de los dos intervalos existentes en la segunda fase. El proceso de eliminación de los dos subintervalos centrales no es sino eliminar los puntos que tengan un 1 en su segundo decimal.
Prosguiendo así, resulta que nos quedamos con todos los puntos que en su expresión decimal no tengan sino ceros o doses. Cualquier número real de la forma 0,200002222020220022022.. pertenece al conjunto de Cantor.
La biyección es ahora la siguiente: a cada número en base tres del conjunto de Cantor le hacemos corresponder un número en base dos resultante de cambiar los doses por unos. Es evidente que se trata de una biyección, pero ahora el conjunto imagen es el intervalo [0,1] completo, pues cualquiera de sus puntos se expresa como una combinación concreta de ceros y unos en su expresión decimal binaria.
Así pues, y a pesar de toda la intuición en contra, tenemos nuestro resultado: no basta que un conjunto tenga la potencia del contínuo para que tenga medida mayor que cero.
22 comentarios
Air jordan shoes -
Nike Dunk Sb -
Ojodeorux -
Perdida -
Me intereso el tema ya que stoy biendo la cardinalidad de las funciones racioanel y las funicnes irracionales, la cual se que las primeras tienen la cardinalidad del continuo y las segundas tienen la cardinalidad de 2 al contunio, lo qu eno se es que "tan" grande grande es una comparada con la otra.
Anónimo -
juan -
alica murillo -
Probar que los reales son equivalentes las partes de los naturales
Crystal -
Pensaba que había sido una demostración de lo más elegante... y llego a los comentarios y me pierdo ;)
Exceptuando, eso sí, la explicación por reducción al absurdo de Mewt, que creo haber seguido sin problemas (pero como no soy matemática, me podéis engañar fácilmente, jeje)
Andy -
TioPetros -
Es más, estoy cada vez más convencido de que tienes razón. Tanto, que voy a eliminar la propuesta de demostración del post dentro de unos días, cuando todos hayan podido ver el error, proque de los errores se aprende. Muchas gracias.
Andy -
Tu prueba es falaz. Aunque creo que Pepe se está liando demasiado con su exposición, el hecho es que, como dice, todos esos extremos son puntos racionales y, por ende, el conjunto de los extremos obtenidos en el límite es numerable, por ser un subconjunto de Q.
Recuerdo que yo también caí en ese argumento tramposo la primera vez que vi la demostración de las propiedades del conjunto de Cantor, pero ver por qué no vale con considerar los extremos no es muy difícil:
Si para cada n, definimos el conjunto An={1,2,3,...2^n}. Su cardinal es 2^n y, sin embargo, no creo que a nadie se le ocurra pensar que el cardinal del conjunto límite sea 2^X0
Visto de otro modo, dado que los extremos se conservan en el proceso de iteración, lo que obtienes en el límite es una unión numerable de conjuntos numerables (finitos, de hecho).
Por cierto, esos puntos de los extremos son exactamente TODOS los puntos que admiten el doble desarrollo ternario comentado en los posts anteriores.
samu -
Podemos concluir por tanto que la representacion de los numeros reales en una base determinada es univoca casi por doquier, no? XD
TioPetros -
Ya hemos mencionado varias veces en este blog que la expresón "casi por doquier" en teoría de la medida (análogo completamente a la de "casi seguro" en teoría de la probabilidad) no esconde ningúna falta de concisión, sino que quiere decir algo muy concreto: el cumplimiento de la propiedad de que se trate en todo punto salvo, a lo sumo en un conjunto de medida cero. (O de probabilidad cero).
Inmersos en la teoría de la medida, decir que una propiedad se cumle cpd es una forma de decir que aquellos casos en los que no se cumplen no tienen peso alguno en el total, salvo por motivos teóricos.
En la teoría de la probabilidad un cumplimiento "casi seguro" nos habilita para dar por hecho tal cumplimiento. Sin embargo sigue manteniendose la nomenclatura porque conceptualmente son dos cosas diferentes un cumplimiento casi seguro y un cumplimiento seguro. (o una propiedad que se cumple siempre, o que se cumple "casi por doquier".
mewt -
0.2 y 0.02222222222222222....
que van a parar a 0.1
¿Que ocurre? pues que en el conjunto de Cantor también hay números con en cuyo desarrollo "trecimal" puede aparecer un 1. Sin embargo, para todos ellos se verifica que despues de este 1 no puede haber ningun otro numero (estos son justamente los extremos de los intervalos que vamos tomando). Asi que todos estos numeros son racionales, y por tanto forman un subconjunto de medida 0, y lo que tenemos, desde un punto de vista estricto de teoria de la medida (date tiempo, samu, que esta es de 5º! ;) ) es lo que se llama una biyeeción casi por doquier, a menudo abreviado como biyeccion cpd, donde lo del cpd despues de una propiedad quiere decir que esta se verifica siempre salvo en un conjunto de medida 0.
En teoria de la medida no importa ninguna de las nociones clasicas que tengas, lo que importa es que las funciones sean "continuas cpd, derivables cpd, biyectivas cpd", etc. Probablemente el autor de la demostracion es un experto en teoria de la medida y ya piensa en todas las cosas de esta forma y ni lo menciona.
En cualquier caso, la aplicacion es sobreyectiva (sobreyectiva de verdad, no cpd), lo cual ya basta para garantizarnos que el cardinal del dominio (el conjunto de Cantor) es mayor o igual que el de la imagen, que es continuo (aleph_1)
Como el carninal de C no puede ser mayor que el del continuo (porque C esta contenido en los reales, que tienen cardinal continuo) pues tenemos la igualdad.
Lo cierto es que la demostracion es mucho mas bonita sin todos estos tecnicismos :-P
samu -
0.01111111 .... = 0.10000.....
¿no plantea alguna dificultad en afiramar que la construccion es una biyeccion?
samu -
Naka Cristo -
Esa demostración por biyección no la conocía y me ha parecido muy buena.
La que dice mewt demuestra que no es numerable, pero no que su cardinal sea C (Sí lo hace si afirmamos la HC)
omalaled -
mewt -
procedemos entonces a contruir un nuevo numero a cuya expresion decimal tiene un 0 en la posición i-ésima si ai tiene un 2, o 2 si tiene un 0. El numero asi construido vuelve a ser un elemento del conjunto de Cantor (porque sólo aparecen ceros y doses en su expansion decimal) y no es nin guno de los an, ya que difiere de cada uno en al menos un digito. Esto es una contradiccion, luego el conjunto de Cantor no puede ser numerable.
Anónimo -
Pero el hecho de que la potencia del contínuo es aleph sub uno, que es igual a dos elevado a aleph sub cero, creo que no tiene discusión.
pepe -
0 -> a
n -> a_n (para n>0)
Resumiendo, la cuestión no es que en la etapa n añadas 2^n elementos (lo mismo puedes hacer con la sucesión a_n tomando primero 2 términos, después 4, después 8, etc.), la cuestión es dónde los añades, añadidos en los sitios correctos, al tomar el cierre te puede salir un conjunto numerable (caso de la sucesión convergente), uno no numerable (como el conjunto de Cantor), o incluso te podría salir todo [0,1], por ejemplo tomando como sucesión a_n una numeración de los racionales de [0,1], y como es obvio, lo de tomarlos en grupos de 2, 4, es claramente opcional.
Un saludo
Palimp -
Igual me he perdido algún post, pero Aleph sub 1=C ¿por definición? ¿no había polémica al respecto?