Métodos

Raíces cuadrada y cúbica a mano (y 2)

Segundo y último post de la serie, en el que Jorge Alonso nos explica razonadamente cómo extraer la raíz cúbica de un número

3.RAIZ CUBICA

3.1. Raíz de 17580

El método a seguir es análogo al que empleamos con la raíz cuadrada.

¿Cuántos dígitos tiene la raíz cúbica de 17580? Como 10³=1000 y 100³ = 1000000, deducimos que son dos:

(10a+b)³ + r = 1000a³ + 300a²b + 30ab² + b³ + r

Vemos que 17580 es aproximadamente 1000³, esto es, a³ es aproximadamente 17, con lo que a vale 2.

Restando el valor de 1000 a³, nos queda

9580=300a²b + 30ab² + b³ + r

Para estimar el valor de b, dividimos entre 300a²:



obteniendo b=7.

Probamos este valor de b:

9580=300·2²·7 + 30·2·7² + 7³ + r = 11683 + r

que no sirve, por lo que pasamos a b=6:

9580=300·2²·6 + 30·2·6² + 6³ + r = 9576 + r

¡Conseguido!:

17580=26³ + 4

Expresándolo de forma compacta, se ve así:



En conclusión:

La raíz cúbica se calcula de forma similar a la cuadrada, pero separando los dígitos del radicando en grupos de tres cifras.

Multiplicación "a la rusa" (2 de 2)

Segundo y último post de la serie de Jorge Alonso sobre este método de multiplicación

Retomemos el ejemplo anterior:

69 x 13
34 x 26
17 x 52
8 x 104
4 x 208
2 x 416
1 x 832

Pero traduzcámoslo a numeración binaria:

1000101 x 1101
100010 x 11010
10001 x 110100
1000 x 1101000
100 x 11010000
10 x 110100000
1 x 1101000000

Como vemos, en base 2 dividir y multiplicar por 2 es sencillísimo:
basta con tachar la última cifra en el primer caso (recordemos que el
resto se ignora), y añadir un cero en el segundo.

El siguiente paso es tachar las filas cuyo primer término sea par, es
decir, que termine en cero:

1000101 x 1101
--------------------
10001 x 110100
--------------------
--------------------
--------------------
1 x 1101000000

Y por último se suma la segunda columna:

+ 1101
+ 110100
+ 1101000000
============
1110000001

Fijémonos que lo que en realidad hemos hecho ha sido

(1 x 1101) + (100 x 1101) + (1000000 x 1101)

que no es más ni menos que

(1 + 100 + 1000000) x 1101

= 1000101 x 1101

Es decir, lo único que hacemos es aplicar una propiedad básica de la
multiplicación:

1000101 x 1101 = (1 x 1101) + (100 x 1101) + (1000000 x 1101)

Si fuese en base 10, esta propiedad la escribiríamos como:

536 = 500 + 30 + 6

536 x 42 = (500 x 42) + (30 x 42) + (6 x 42)

Desesperación matemática

Feliz fin de semana a todos los lectores de este blog.

Resolución por recurrencia.

Hemos ido viendo varias herramientas para resolución de problemas que en principio parecen difíciles, pero que se disuelven en la más meridiana claridad después de ser enfocados desde una perspectiva conveniente para ellos. Vimos el principio de correspondencia, que convertía por arte de magia algunos problemas muy difíciles en apariencia en cuestiones sencillísimas si era bien aplicado. Comentamos en su día que este método tiene un precio: para si aplicación no existen más fórmulas que la agudeza mental y la habilidad.

Otro método muy corriente y de resultados magníficos si es bien empleado es el de recurrencia .

El método de inducción para demostrar afirmaciones que implican a los números reales consistía en demostrar la afirmación para n=1, y demostrar que si se cumple para n, se cumple necesariamente para (n+1). Pues bien; en cierto modo, la resolución de problemas por recurrencia es la inversa de la inducción. Me explico:

Cuando debemos encontrar la solución de un problema para cualquier valor de uno de sus parámetros enteros, si abordar el problema directamente nos es imposible podemos hallar la solución para N= n en función del valor de la solución para N=(n-1). A veces esto no será posible, y la función solución deberá ser expresada en función de varios valores anteriores , no de uno solo. Cuando tengamos expresada esta relación de recurrencia, más el calor inicial o los valores iniciales necesarios, diremos que la función objetivo está ya definida de forma recursiva .

En efecto, la función, a pesar de su apariencia extraña, definida en función de sí misma, está perfectamente definida. El paso de la forma recursiva a la forma habitual en función del parámetro n puede no ser trivial, y necesitar de ciertas herramientas algebraicas, pero esa es otra cuestión.

Vemos un ejemplo de un problema aparentemente dificil resuelto de por recurrencia.


Si trazamos una serie de rectas en un plano, sin orden ni concierto alguno, ¿en cuántas regiones queda dividido el plano?


Cuando trazamos al azar, la probabilidad de que dos rectas sean paralelas es nula, así como la probabilidad de que tres rectas se corten en el mismo punto, así que supondremos esta situación: no hay rectas paralelas, ni puntos de corte de más de dos rectas.

Por la ilustración podeis ver que la cuestión es algo enmarañada en apariencia. Pensemos que tenemos ya (n-1) rectas y dibujamos la número n. Como no hay paralelas, nuestra nueva recta cortará a las (n-1) actuales en (n-1) puntos, que la dividirán en n trozos. Dos de estos trozos serán semirectas infinitas y el resto simples segmentos. Lo que es muy fácil e ver es que cada uno de estos n trozos de recta dividen una región en dos, por lo que nuestra nueva recta incrementará en n el número de regiones del plano.

Expresado en fórmulas: siendo R_n el número de regiones pedido:

R_n = R_n-1 + n
R₁ = 2 (condición inicial).

Esta es la definición recursiva de nuestra función objetivo. Como no necesitamos más que una llamada a la propia función en un valor anterior, necesitamos una sola condición inicial: el plano es dividido en dos regiones por la primera recta.

Una mínima manipulación en este caso nos lleva a la expresión de R_n en función de n:

R_n = R₁ + [ n + (n-1) + ... + 2 ]

R_n = 1 + [n(n-1)]/2.

El problema que vimos hace algunos meses de los apretones de manos también puede ser resuelto de forma recursiva sin ninguna complicación. En todo caso, obtenemos una definición recursiva de la función objetivo del problema, que condensa toda la información de la misma, aunque no está expresada de la forma habitual. Encontrar esta forma habitual (dependencia funcional del parámetro n) es tarea de dificultad muy diversa. Era caso trivial en nuestro ejemplo, y en otros casos es bastante más complicado. Aún así, cuando no podemos o no sabemos encontrar dicha forma normal, si tenemos la definición recursiva , tenemos resuelto el problema.

Así multiplicaban los árabes en el siglo XIII

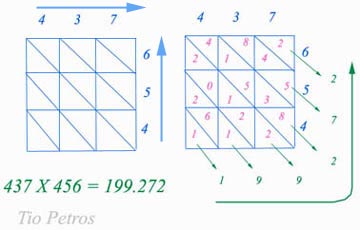Algunos conocimientos matemáticos son indispensables para desenvolverse en el mundo. Y de estos, los algoritmos de suma, resta, multiplicación y división (las cuatro reglas) son el mínimo imprescindible. Un algoritmo es una colección de reglas para obtener un resultado a partir de unos datos. Si se siguen correctamente los pasos, llegamos al resultado correcto, aunque no sepamos los motivos por los cuales el algoritmo es como es y no de otra manera.
Luca Pacioli recoge en su Summa de arithmetica, geometria, proporzioni et proporzionalita , editado en Venecia en 1.494; un procedimiento árabe del siglo XIII para obtener el producto de dos números de cualquier cantidad de cifras, que se aparta del habitual que conocemos, si bien es completamente equivalente a éste.
Intentando ser fiel a la propuesta inicial de apartarme del tópico, les voy a explicar en qué consiste dicho algoritmo.
El ejemplo de la imagen multiplica 437 X 456. Como ambos números tienen tres cifras, se parte de un cuadrado subdividido en 3x3 celdas, y se subdivide cada celda como se indica en la figura de la izquierda. Uno de los números a multiplicar se escribe sobre el segmento superior escrito en sentido habitual, y en otro en el lateral, de abajo arriba.
En cada celda se escribe el producto de los dígitos correspondientes, colocando las unidades en la subcasilla superior, y las decenas, si las hubiere, en la inferior.
Se suma diagonalmente, acarreando a la diagonal siguiente las llevadas, si las hubiere.
El resultado aparece en las sumas de las diagonales, en el sentido que indica la flecha verde.
Puede parecernos un método exótico, pero es fácil comprobar que en esencia no se diferencia demasiado de nuestro método habitual.

____________________________________________________________________

Por cierto, no viene nada mal reivindicar la figura de Luca Pacioli, uno de los grandes hombres del renacimiento italiano. Pueden ver un soberbio retraro que le realizó Jacopo de Barbari en 1495, un año después de ver publicada su Summa arithmetica .

El principio de correspondencia.

Nunca con tan humilde herramienta se consiguió tanto.

Uno de los atributos que puede tener una demostración matemática es la elegancia. Este atributo forma parte de ese conglomerado de cualidades que reunimos bajo el nombre de belleza, y que aunque no sabemos definir, percibimos perfectamente.

La elegancia de una demostración es una de las cualidades más objetivas dentro de todas ellas, y tiene mucho que ver con la longitud de la demostración: cuanto más concisa sea, será más elegante. Desde luego, una demostración bien hecha es incontrovertible, y expresa una verdad inmutable dentro de su campo de definición; pero hay demostraciones bellísimas, y otras que no lo son. Cuando vemos la matemática no sólo como una herramienta para comprender el mundo, ni siquiera como una forma de acceder a ciertas verdades, sino como una aspiración estética, no nos conformamos con saber un hecho, sino con el placer que nos produce su conocimiento, y sobre todo el camino recorrido para acceder al mismo.

Lo mismo sucede con un ajedrecista que no se conforma con ganar una partida (supuesto fin del juego, no lo olvidemos). Juega porque ama el juego, y sabe que hay partidas ganadas que son chapuceras; y partidas bellas incluso entre las perdidas.

El Principio de correspondencia es una humildísima herramienta que puede ser utilizada de forma celestial produciendo enorme elegancia en muchas demostraciones combinatorias.

Es algo tan tonto como esto:

Dos conjuntos finitos cuyos elementos pueden ponerse en correspondencia uno-uno, son del mismo tamaño.

Cuando tenemos que calcular el tamaño de un conjunto, podemos encontrar otro de su mismo tamaño más fácil de medir. Ese es todo el misterio. Lo bueno es que los problemas se pueden simplificar sorprendentemente si elegimos un buen conjunto auxiliar.

Pongamos un par de ejemplos.


En una liga de n equipos de fútbol se deben jugar partidos eliminatorios hasta que quede uno solo, que será el campeón. Cada partido acaba con la victoria de un equipo, pues se llega si es necesario a los penaltis. Si en un momento el número de equipos es impar, se queda uno al azar sin jugar esta etapa, pasando automáticamente a la siguiente. ¿Cuántos partidos se deberán jugar en toda la liga?

1.- RESOLUCIÓN POR CONTEO DIRECTO.

Si el número de equipos fuera potencia de 2, pongamos 2^k, el cálculo sería muy sencillo. En primera fase se eliminarían n/2=2^k-1, la segunda n/4=2^k-2, las sucesivas n/8, n/16... hasta llegar a la final en la que habrá 2 equipos a jugar, y se eliminaría uno. La suma será 2^k-1+2^k-2+...+1=2^k-1= n-1.

Cuando el número de equipos inicial no sea potencia de dos, la cosa se complica: unas veces será par el número de equipos, y otras será impar, con lo que el tratamiento deberá ser diferente. No se trata de un problema insalvable, pero complica extraordinariamente el cálculo. Al final llegaríamos al resultado de que se jugarán siempre (n-1) partidos.

2.- RESOLUCIÓN MEDIANTE EL PRINCIPIO DE CORRESPONDENCIA.

Cada partido supone la eliminación de un equipo. Cada equipo eliminado lo ha sido en un partido. Luego el número de partidos será igual al número de equipos a eliminar: (n-1).

En un renglón hemos demostrado con total generalidad el problema, sea cual sea el número inicial de equipos. Esta es más elegante que la anterior, ¿verdad?

Otro ejemplo:

¿Cuántos subconjuntos tiene un conjunto de n elementos?

1.- RESOLUCIÓN POR CONTEO DIRECTO

Contaremos los subconjuntos existentes para cada tamaño de los posibles. De tamaño cero habrá un subconjunto: el vacío. De tamaño 1 habrán n subconjuntos. En general, de tamaño k, con k menor o igual que n habrá un número de subconjuntos igual a las combinaciones de n tomados de k en k. Extendiendo dicha suma desde cero hasta n comprobaremos que la expresión resultante es 2ⁿ.

2.- RESOLUCIÓN MEDIANTE EL PRINCIPIO DE CORRESPONDENCIA.

Para cada subconjunto, un elemento del conjunto inicial tiene dos posibilidades: pertenecer o no al subconjunto. El número de subconjuntos será igual al tamaño del conjunto de posibilidades cruzadas de los n elementos, que es obviamente 2ⁿ.

Ya me dirán ustedes si no es enorme la utilidad de una herramienta tan simple. Lo que no es simple, es encontrar el conjunto útil para el conteo; ahí reside la inteligencia de la demostración, y a veces incluso la genialidad.

Todos los blogs del mundo están alojados en Blogia.

El método de inducción matemática es una herramienta muy potente de demostración. Cuando tenemos una afirmación que atañe a un conjunto numerable de objetos, podemos demostrar que todos ellos cumplen una determinada propiedad demostrando dos cosas:

1.- Que la cumple el primer objeto.
2.- Que si la cumple el n-ésimo, entonces también la cumple el (n+1)-ésimo

La hipótesis de que la cumple el n-ésimo no hace falta demostrarla, y se llama hipótesis de inducción.

¿Porqué funciona este método para todas los objetos, quizás infinitos, del conjunto de estudio? Funciona por "efecto dominó": si conseguimos demostrar para n=1, entonces debe ser cierta para n=2 aplicando la segunda cláusula de la demostración, pero si se cumple para n=2, volviéndola a aplicar debe cumplirse para n=3...y esta situación es extrapolable a todo el conjunto, mientras este sea numerable.

Sin embargo, este método debe usarse con cuidado. Veamos una demostración falsa basada en el método de inducción:

Demostraremos la afirmación:

TODOS LOS BLOGS DEL MUNDO MUNDIAL ESTAN ALOJADOS EN BLOGIA

Conseguiremos demostrar este absurdo demostrando que si en un conjunto de blogs existe un blog alojado en blogia, entonces todos lo están. Una vez demostrado esto, aplicando tal afirmación al conjunto de todos los blogs del mundo, tenemos demostrada nuestra efirmación.

PRIMER PASO: n=1

Es evidente que en un conjunto de un solo blog se cumple que si existe un blog alojado en blogia, entonces todos lo están. Es incuestionable.

SEGUNDO PASO: SI SE CUMPLE PARA n, SE CUMPLE PARA n+1

Asumamos por hipótesis de inducción que se cumple para n: Si un conjunto de n blogs tiene uno alojado en Blogia, todoas están alojados en Blogia. Tomemos ahora un conjunto de (n+1) blogs. Quitamos un blog de forma que quede al menos un blog de Blogia en el conjunto. Como tenemos ahora n blogs, por hipótesis de inducción todos ellos están alojados en blogia. Sacamos un blog de este conjunto (que ovbiamente será de blogia), e introducimos el que habíamos casado antes. Volvemos a tener n blogs con al menos uno de Blogia, luego todos lo son. Ahora introducimos el que teníamos fuera, que sabemos es de Blogia, y tenemos el conjunto de (n+1) blogs, todos ellos alojados en Blogia.

Cumplidas las dos condiciones, tenemos demostrado que si un conjunto de blogs tiene al menos uno en blogia, todos lo están, luego el conjunto de todos los blogs del mundo mundial también cumple esta propiedad. Dado que al menos este blog (Tio Petros) está alojado en Blogia, concluimos que Todos los blogs del mundo están alojados en Blogia.

Puede el lector encontrar el fallo del razonamiento?