La entropía de Kolmogorov
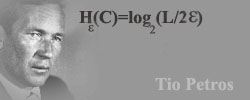Para un servidor una de las mayores incógnitas del concepto de entropía es el motivo por el que tantas veces se emplea como comodín para las más peregrinas explicaciones. El concepto tiene un feeling indiscutible, pero lo malo es que transciende al mundo coloquial sin rigor alguno. Es de buen tono introducir la palabra entropía, aunque no se sepa muy bien a qué nos estamos refiriendo. Así, pude oír hace algunos años al escritor Fernando Sánchez Dragó manifestarse contra las corridas de toros porque añadían sufrimiento a la entropía del universo. El concepto al que hacía referencia de forma inadecuada, pueril y sin rubor alguno era evidentemente el concepto físico. En este ámbito, si un tertuliano quiere destacar no tiene más que unir el vocablo ciertamente eufónico de entropía al vocablo universo para obtener ...una frase redonda sin sentido alguno. (Me temo que este comentario es un poco off topic en Tio Petros).Tenemos también el concepto de entropía en laTeoría de la información de Claude E. Shannon. Es una extrapolación del concepto a otro ámbito, y tampoco de esta entropía queremos hablar ahora.
Cuando Shannon publicó sus trabajos hacia 1.948, a los matemáticos en general les pareció algo excesivamente orientado a la tecnología como para tener interés en matemática pura. El gran Andrei Nikolaievich Kolmogorov fué la excepción, escribiendo en una ocasión:
La importancia del trabajo de Shannon para los matemáticos puros no fue totalmente apreciada desde el comienzo. Recuerdo cuando, en el Congreso Internacional de Matemáticos celebrado en Ámsterdam en 1.954, mis colegas norteamericanos, especialistas en probabilidades, creían que mi interés por los trabajos de Shannon eran algo exagerado ya que esto era más tecnología que matemática. Ahora, tales opiniones ni siquiera necesitan ser refutadas
De esta forma, y dada la inmensa y merecida reputación de Kolmogorov, le fue posible extender las nociones de Shannon a la matemática más abstracta. Concretamente estableció la definición de entropía en el interior de un conjunto.
Dado un conjunto, es necesario utilizar cierta cantidad de información para delimitar sin ambigüedad cualquiera de sus subconjuntos propios. Kolmogorov entendió que aquí era donde podía entrar el concepto de entropía. Definió la entropía de un subconjunto en función del hecho anterior, y la llamó e-entropía. (Léase épsilon-entropía).
Si C es un conjunto finito, podemos expresar por enumeración la lista de sus subconjuntos. A cada subconjunto le corresponderá simplemente su número de orden en la lista. El tamaño de la lista es de 2 elevado a N subconjuntos. Lo que expresado en sistema binario nos ocupa precisamente N bits. (Otra forma de verlo es teniendo en cuenta que podemos hacer corresponder un bit a cada posible elemento de los N en C , y para un subconjunto concreto, el j-ésimo bit vale 1 si está presente en el subconjunto, y 0 en caso contrario).
Kolmorogov definió la entropía de un subconjunto como
H(C)= log (N)
donde el logaritmo está en base 2.
Para conjuntos no numerables su táctica fue el uso de e-recubrimientos de radio e (épsilon) arbitrario. La epsilon-entropía del subconjunto era al igual que en el caso numerable, el logaritmo en base 2 del número de elementos del e-recubrimiento mínimo para cubrir totalmente al conjunto. Un e-recubrimiento del conjunto C es un recubrimiento por conjuntos de diámetro menor o igual a 2e. En el caso se un segmento de recta, el número de elementos de un e-recubrimiento es precisamente (L/2e), de donde su e-entropía será:
H(C)=log (L/2e) , fórmula que adorna la foto que encabeza este artículo, en la que aparece el gran Kolmogorov, de quien nos ocuparemos en un artículo futuro.
De esta manera, Kolmogorov hecha un puente entre la teoría de la información y la abstracta teoría de conjuntos.
8 comentarios
Generic Cialis -
antikaria -
Quizá es aplicable que 'no se hizo la miel para la boca del asno'.
marco -
marco -
gracias saludos desde peru
Fernando Cortázar -
Ánimo desde Madrid
yesenia -
edir -
Cosimo -