Razonamientos geométricos.
 Comentamos hace algún tiempo que existen personas empeñadas en demostrar lo imposible. En aquel momento hablábamos de los ingenuos trisectores de ángulos. Este tipo de falsas demostraciones suelen ser casi siempre demostraciones geométricas, lo que pudiera dar pie a pensar que las demostraciones que se basan en conceptos geométricos no son seguras.
Comentamos hace algún tiempo que existen personas empeñadas en demostrar lo imposible. En aquel momento hablábamos de los ingenuos trisectores de ángulos. Este tipo de falsas demostraciones suelen ser casi siempre demostraciones geométricas, lo que pudiera dar pie a pensar que las demostraciones que se basan en conceptos geométricos no son seguras.Nada más lejos de la realidad. Lo que sucede es que muchas veces confundimos razonamiento geométrico con razonamiento a bulto, a ojo o al "poco más o menos". Una demostración basada en conceptos geométricos puede ser tan perfectamente válida como la fundada exclusivamente en manipulaciones algebraicas.
Basta con no dar un paso antes de asegurarse de la licitud del mismo. Las figuras deben servir para orientarnos, no para desorientarnos, y son los razonamientos lo que nos habilitan para aceptar proposiciones como ciertas, no los dibujos.
Será por eso que una de las vertientes más divertidas de la matemática recreativa es la de las presuntas paradojas geométricas. Dado que virtualmente cualquier tema aritmético admite una interpretación geométrica, siempre es posible hacer un dibujo para ejemplificarlo. Hablemos de uno de tales divertimentos, que espero no sea demasiado conocido por mis lectores (yo ya me lo he encontrado bastantes veces por la web).
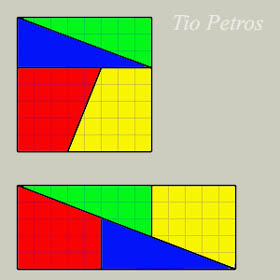
Sabemos que una de las propiedadesd de las areas de las figuras geométricas, como medidas que son, es que son invariantes por traslaciones. Así, si troceamos un cuadrado y con los trozos recomponemos un rectángulo, es de esperar que ambos tengan el mismo área. Sin embargo, en nuestra figura, los 8x8=64 unidades cuadradas del cuadrado se convierten en 13x5=65 en el rectángulo.
Encontrar el error no es demasiado difícil, pero a mi juicio lo más interesante es lo bien que este ejercicio ejemplifica los peligros de un razonamiento geométrico no riguroso. Todo el mundo sabe que un metro cuadrado no puede aparecer por arte de magia, y que algo debe estar mal; pero si el error hubiera sido menos vistoso, hubiera pasado desaparecibido. Eso es lo que ocurre con las demostraciones falsas de teoremas imposibles, tales como la cuadratura del círculo, la duplicación del cubo o la trisección del ángulo de 60o
Feliz fin de semana a todos.
Por cierto; les invito a que encuentren de dónde sale una unidad cuadrada de más en el rectángulo, tras unir las cuatro piezas del cuadrado...
14 comentarios
marco -
jessica paola nuéz genes -
Aliena -
Francoise Niclous Golpier -
Shunt -
Anónimo -
Adrian -
hay que mirarlo con unasgafas detectoras de mentiras
Sam Berimbad -
Pérez -
Tio Petros -
MikeCT -
Un saludo
Sam Berimbad -
Tio Petros -
No sólo no me supone ningún problema: me encanta. Sobre todo me encanta que te guste. Un cordial saludo
worm -