Contra la pseudociencia: teorema de Tales
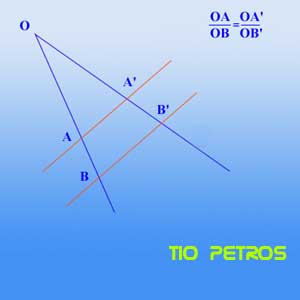Si dos o más paralelas son cortadas por dos transversales, aquellas determinan en éstas segmentos proporcionales THALES DE MILETO. (y Les Luthiers)Hace algún tiempo, cuando hablábamos de topología, decíamos que ciertas propiedades de un objeto geométrico variaban cuando lo torturábamos de determinada manera, y ciertas otras no.
Las formas de tortura a las que puede ser sometido un objeto geométrico son muy variadas. Imaginémonos un triángulo que reposa sobre el plano cartesiano. La forma más leve de molestia que le podemos ocasionar es desplazarlo de un lugar a otro. Algo más molesto para el triángulo será rotarlo. Ambos movimientos son rígidos en el sentido de que mantienen las distancias relativas de los puntos del triángulo, y por lo tanto sus medidas ordinarias. A este tipo de transformaciones se le denomina precisamente movimientos .
Si consideramos la propiedad de triángulo original "tener un área determinada" , o "tener los tres lados de una determinada longitud " , la molestia que hemos ocasionado al triángulo por medio del movimiento no es una molestia lo suficientemente fuerte como para variarlas. Sin embargo si consideramos la propiedad " tener su baricentro en un determinado lugar , evidentemente sí será variada.
Parece intuituvo pensar que aquellas propiedades que resultan invariantes ante una detreminada actuación sobre la figura son propiedades más profundas de la misma, más interesantes, más intrínsecas y menos circunstanciales. En efecto, la propiedad " tener su baricentro en un determinado lugar no parece ser muy importante...
El tipo extremo de tortura a que puede ser sometido un cuerpo geométrico ( y humano, por supuesto) es la pulverización, rasgado, rompimiento y descuartizamiento completo. La geometría (1) no considera tal actuación como civilizada y no se interesa por su aplicación, ya que no hay propiedad tan profunda que permanezca invariante ante tamaña atrocidad. Las máximas torturas "políticamente correctas" en geometría son los homeomorfismos topológicos, que admiten ampliaciones, reducciones, estiramientos, encogimientos y crueldades similares... todo menos romper, rasgar y/o pegar partes. Sólo las propiedades más profundas de la figura permanecerán invariantes ante estas transformaciones, y serán llamadas propiedades topológicas de la figura.
A medio camino están las transformaciones que admiten movimientos, rotaciones y ampliaciones o reducciones ( cambios de escala). Las propiedades que permanezcan invariables serán denominadas " invariantes por cambio de escala"
En una ocasión tuve que explicar trigonometría plana a una persona en media hora (antes de un exámen), cuyos conocimientos eran prácticamente nulos. Opté por hablarle del Teorema de Tales , y decirle que existían ciertas propiedades de un ángulo en un triángulo rectángulo que no cambiaban con la escala: éstas eran cocientes de dos longitudes,en virtud de dicho teorema. Como no importaba a qué distancia del vértice considerábamos los lados cuyas longitudes medíamos, llegábamos a la conclusión de que dichos cocientes eran simplemente propiedades de dichos ángulos. Dado que había tres lados posibles, teníamos seis maneras de hacer las divisiones. Simplemente les poníamos nombre: seno, coseno, tangente, cotangente, secante y cosecante. Las relaciones entre ellos eran una trivialidad que además no hacía falta alguna aprender; salían solas aplicando el teorema de Pitágoras.
Hay veces que uno vé iluminarse una cara con el entendimiento repentino: esa fue una de las veces. Aquella persona había comprendido perfectamente la invarianza por cambio de escala, y de paso la trigonometría había dejado de ser símplemente una palabra griega de seis sílabas para convertirse en algo muy, muy sencillo.
Algo así hubiera necesitado el protagonista de la siguiente historia, rigurosamente cierta, en la que participé hace bastantes años.
La charla había discurrido por los cauces esperables, dado el cartel anunciador: ANTROPOLOGIA GNOSTICA. EL MISTERIO DE LAS PIRÁMIDES. En un segundo piso, una salita con unas treinta personas escuchaban a un orador explicar mil y una idioteces sobre las medidas de la pirámide de Keops. Que si dividiendo tal arista por tal otra sale x veces el diámetro terrestre, que si patatín y que si patatán. Imposibilidades dimensionales aparte (nunca se puede comparar un cociente de dos longitudes con una longitud), el muchacho cabrón con ganas de guerra esperaba agazapado en su silla urdiendo el ataque. Algunas de las medida de la pirámide que el orador equiparaba con distancias y valores del mundo real que los egipcios ( se supone) no podían conocer eran medidas lineales (en metros), y otras eran cocientes de medidas, y adimensionales por tanto. Las primeras no era invariantes por cambio de escala y las segundas sí, por razones expuestas más arriba.El muchacho cabrón levanta la mano en el turno de preguntas:
- He oído, dice, que la Gran Pirámide está en parte cubierta por arena del desierto, de forma que puede ser mucho más grande de lo que creemos, a pesar de que ya nos parece inmensa; es esto cierto?
- Por supuesto que sí es cierto, explica con fervor el orador. Puede ser aún mucho mayor de lo que creemos.
Ya ha mordido el anzuelo, el pobre imbécil, piensa el muchacho cabrón.
- Y si es así, cómo podemos decir que la distancia tierra-sol es EXACTAMENTE nosecuántas veces la altura de la pirámide, si no sabemos cuanto mide dicha altura?
Ya está. Comienzan murmullos al fondo de la sala. El orador carraspea y el público se ríe tímidamente al principio, y más abiertamente después. EL muchacho piensa para sí: ¿Porqué disfruto yo tantísimo con estas cosas?
____________________________________________________________
(1) Consideramos en este post geometría en el sentido de Felix Klein: el estudio de las propiedades que permanecen invariantes ante determinadas transformaciones. Desde este punto de vista, una transformación que no deja invariante propiedad alguna no tiene interés geométrico.
12 comentarios
yo -
NNN -
anonimo -
JAVIER -
Anónimo -
Jean Paul -
TioPetros -
Goyo -
Dem -
Lola -
Un amigo me contó una anécdota en la que fue acompañado a una de estas reuniones (una que trataba sobre la reencarnación), y su acompañante hizo una pregunta un tanto comprometedora sobre el déficit de almas actual, y el resultado fue que los echaron de allí.
Matías -
Bien hecho. ^^
oniric -
Concha