Triángulos sobre una cuadrícula (y 2)
 Vamos a exponer una de las posibles demostraciones de que es imposible dibujar un triángulo equilátero con vertices en los puntos de una cuadrícula, como exponíamos en el post anterior. Como bien ha sido expuesto en los comentarios de ese post, la cuadrícula se supone ortogonal. Cada lado de la cuadrícula elemental se toma como unidad de medida.
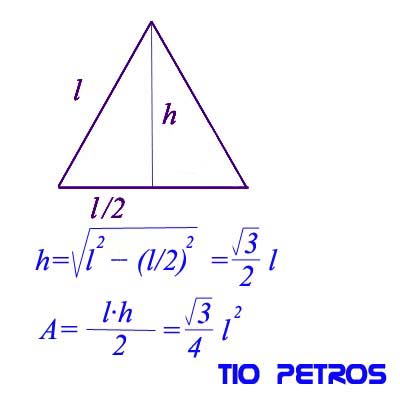
Vamos a exponer una de las posibles demostraciones de que es imposible dibujar un triángulo equilátero con vertices en los puntos de una cuadrícula, como exponíamos en el post anterior. Como bien ha sido expuesto en los comentarios de ese post, la cuadrícula se supone ortogonal. Cada lado de la cuadrícula elemental se toma como unidad de medida.En la ilustración que encabeza el presente post se demuestra que el área de un triángulo equilátero, es raíz de tres cuartos del cuadrado del lado.
El cuadrado del lado es siempre un número entero por aplicación directa del teorema de pitágoras, y en tales circunstancias, el área de un triángulo equilátero sobre la cuadrícula será siempre un número irracional por la presencia de la raiz de tres.
Ahora bien, todo triángulo con vértices sobre la cuadrícula tiene área racional. Para demostrarlo, dibujemos el menor cuadrilátero en la cuadrícula que contenga completamente a dicho triángulo. Son posibles dos casos: que el triángulo tenga sus tres vértices en la frontera del cuadrilátero mínimo que lo contiene, o que tenga sólo dos. Ver la ilustración siguiente:

En el primer caso, el area sobrante se divide en tres triángulos rectángulos; en el segundo en tres triángulos rectángulos más un cuadrilátero menor. El área de los triángulos rectángulos de en la cuadrícula es siempre racional, por ser su área base por altura entre dos, siendo tanto la base como la altura horizontales y verticales de la cuadrícula, y por lo tanto enteros. El área del subcuadrilátero será no sólo racional, sino entera, por ser el producto de dos enteros (base y altura).
Dado que el área del cuadrilátero que contiene al triángulo también es entera, restando áreas obtenemos que en todo caso un triángulo dibujado en una cuadrícula tiene área racional.
Por lo tanto nunca un triángulo equilátero podrá ser dibujado sobre la cuadrícula.
Esta no es sino una de las posibles demostraciones.
16 comentarios
HINATA -
cesar -
gracias
GJFGRTRTURTURTRTRTRTRTURTURTURTU -
manuel yuyinn -
melisa -
julio -
pau -
TioPetros -
Tu demostración vale perfectamente para ello, pero racional, no entera. La mitad de un entero puede ser entero, y puede no serlo...
Killerrex -
Una demostración tonta de que el área de un triángulo cualquiera definido sobre una cuadrícula tiene siempre area entera se puede obtener de la relación entre producto vectorial y area comprendida por los vectores.
Básicamente si tenemos 2 vectores definidos por 4 números enteros (a,b) y (c,d) el área del paralelogramo que definen es a*d-b*c que no puede ser de ninguna forma un número irracional... y por extensión el del triángulo que sería la mitad del paralelogramo
Curioso blog, creo que puedo aficionarme :-)
BitFarmer -
El texto viene a decir que de donde ha salido el hueco extra en la segunda figura, y os aseguro que pase unos angustiosos minutos comparando ambas figuras en busca de una respuesta!
http://www.hcsoft.net/sergio/trianglar.pdf
TioPetros -
Palimp -
Carlos -
Carlos -
Demostrar que en un triángulo de lados a,b,c y área T :
1- se verifica a^2 + b^2 + c^2 >= 4*sqrt(3)*T
2- ¿En qué caso se verifica la igualdad?
mewt -
Y para calcular el area del triangulo equilatero tambien se podia haber usado la formula de Henon, que nunca nadie se acuerda de ella :-P
Duende -
Es interesante ver el interés que despiertan tus posts en gente con distinto nivel en ciencia, además de que incluyes otros temas para no resultar aburrido. Sigue así.
Saludos,
Duende