Maraña de rectángulos
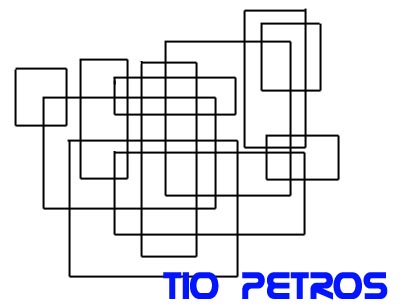Les propongo un problema que acabo de encontrar:Tenemos un cierto número de rectángulos distribuidos sobre una superficie plana. Existe total libertad en la forma de los mismos, y en la disposición en el plano. Se pueden superponer, intersectar y todo lo que ustedes quieran. Una vez colocados, dividen el plano en una serie de regiones finitas. Denominaremos "región" en este contexto a cada una de las menores divisiones del plano, es decir: a las áreas finitas que no están a su vez subdivididas .
Si sabemos que una de tales disposiciones de rectángulos tiene 18.769 de tales regiones, ¿cuál es el mínimo número de rectángulos utilizados?
19 comentarios
Jesús -
n: 1 2 3 4 ....
Recintos: 2 6 14 26 ....
y es un desarrollo combinato
rio seguro.
BitFarmer -
Lo curioso es que intentando buscar un caso lo mejor posible con rectangulos sin girar, encontre un sistema simple que nos da justo 18769 regiones (sin contar la exterior) con 137 rectangulos.
Por eso me huelo que quizas el problema original se referia a sin girar, y la solucion que encontre debia ser la buscada en el problem "sin girar".
Mi solucion es esta: Inicialmente empezamos con un cuadrado, entonces le añadimos un rectangulo un poco mas estrecho y mas alto, centrado respeto al inicial, y luego le añadimos otro igual pero en vertical, quedando una cruz con sus 4 puntas saliendose del cuadrado original. Luego se repite con otra cruz un poco mas estrecha y mas alta, y asi indefinidamente.
Lo curioso es que, cada nuevo rectangulo, añde exactamente 2 regiones mas que el anterior (el primero una region, el segundo añadio 3, el siguiente 5, etc.).
Si sumamos esta serie, resulta que la suma de los primeros 137 termnos vale exactamente 18769 como os comente.
Alguien tiene una solucion mejor con rectangulos sin girar, o una demostracion de que no la hay? Yo no.
Jesús -
Jorge Alonso -
Yo había dibujado series de rectángulos formando una estrella, todos concéntricos y girados una fracción de vuelta del total; obtenía la fórmula 1+2n(n-1).
Al pasarlos a cuadrados, entonces la fórmula cambia a 1+4n(n-1).
TioPetros -
Por cierto, none: a mi me sale que el número mínimo es una unidad menor que los 69 que propones. Y es una lástima; el 69 es mucho más bonito que el 68. No tiene ni comparación...
mewt -
Asi que mi ecuacion se modifica a
R = 2 + 4N(N-1)
La disposicion donde todos los rectangulos se cortan dos a dos en 8 puntos tambien es posible, tomando rectangulos congruentes con centro fijo y haciendolos girar multiplos fijos de un angulo lo bastante pequenyo...
Ardo en deseos de ver tu solucion :-)
none -
none -
Tio Petros -
el numero de regiones sera maximo cuando lo sea el numero de intersecciones entre los rectangulos
Sin embargo, el máximo número de intersecciones entre dos rectángulos no es cuatro, sino ocho...
Mañana pongo mi solución.
mewt -
El numero maximo de intersecciones es entonces menor o igual a 2N(N-1) (4 veces el numero de parejas de rectangulos). Ademas, podemos alcanzar la igualdad con facilidad, incluso usando rectangulos paralelos, que vamos haciendo cada vez mas estrecos y mas altos (si Tio Petros se anima, que ponga un dibujo). Tambien puede garantizarse la existencia de esa disposicion maxima usando algunos teoremas de geometria diferencial, pero en este caso no es necesario... Total, que nuestro numero maximo de regiones es
R = 2 + 2N(N-1)
Ahora, basta sustituir R por el valor de regiones que queramos (las 18000 y pico) y despejar N en la ecuacion de segundo grado resultante, quedandonos con el N entero inmediatamente posterior a la solucion positiva. La determinacion del numero preciso queda como ejercicio al lector ;-)
mewt -
Supongamos que tenemos N rectangulos en una posicion generica, y sea R el numero de regiones que determinan. El dibujo que forma esta maranya de rectangulos es un grafo plano, que tendra L aristas y V vertices, por lo que debe verificarse la formula de Euler R-L+V=2
(estamos teniendo tambien en cuenta la region exterior, si no queremos contarla, cambiamos el 2 por un 1) de donde tenemos que R=2+L-V
Sea I el numero de puntos de interseccion que se forman al dibujar los rectangulos. Cada uno de estos puntos nos divide cada uno de los dos lados que den lugar al punto de interseccion en 2. Originalmente hay 4 lados por cada rectangulo, de manera que
L = 4N + 2I
Ademas, cada rectangulo nos proporciona 4 vertices, y cada punto de interseccion otro mas, asi que
V = 4N + I
por lo que el numero de regiones es
R = 2 + 4N + 2I - 4N - I = I +2
Con lo que queda claro que el numero de regiones sera maximo cuando lo sea el numero de intersecciones entre los rectangulos. Para resolver el problema solo tenemos que contar el numero maximo de intersecciones.
Dada una pareja cualquiera de rectangulos, es facil comprobar que el numero maximo de intersecciones que se pueden producir entre ellos es de 4. Asi, el numero maximo de intersecciones se produce cuando cada rectangulo corta a todos los demas en exactamente 4 puntos, y ademas todas estas intersecciones sean diferentes. Eso significa 4 intersecciones por cada pareja de rectangulos; como hay N(N-1)/2 parejas de rectangulos, tenemos que el valor maximo de I es
I
Jorge Alonso -
Sólo se me ha ocurrido colocarlos en forma de estrella. Si mis deducciones no son erróneas, con 97 rectángulos se obtendrían 18625 regiones, y 19013 para 98.
Tio Petros -
mewt -
me lo callo por ética acertijera y porque me estan esperando para tomarnos unas pintas ;-) si nadie habla en contra, o da la solución antes, mañana por la mañana posteo...
Tot ziens!
TioPetros -
Este problema me lo han pasado esta mañana, y tengo MI solución, que creo que es LA solución.
Dem -
Es sólo por tocar un poco la moral, porque la verdad es que no sé por dónde coger este problema ;P
xhantt -
TioPetros -
Me parece que la afirmación de que cada rectángulo puede duplicar el número de zonas es una afirmación muy fuerte para ser admitida así, sin más...podrías proponer un rectángulo que duplique el número de zonas de la ilustración de este post???
BitFarmer -
Mi razonamiento es demasiado simple, por eso no creo que sea el definitivo: Cuando ponemos un rectangulo, dividimos el plano en dos zonas (dentro y fuera), y a partir de aqui, cada vez que añadimos otro rectangulo, en el mejor de los casos (que la frontera pase por dentro de cada region), se duplica el numero de areas (pueden dividirse en mas de dos algunas areas, ver nota al final).
Como 2^14 es 16384, con 14 rectangulos a lo sumo tendremos 16384 regiones, es insuficiente, asi que minimo 15 rectangulos se necesitarian.
Pero mi duda es... hay alguna disposicion de los rectangulos conforme se añaden de forma que cada vez que añadimos uno este divida cada region existente en dos?
Otra aclaracion: Existen maneras de que un rectangulo nuevo divida a una region existente en mas de dos nuevas regiones, pensar en una region con forma de "peine", de forma que un nuevo rectangulo podria separar cada una de las puas y generar muchisimas regiones... pero para construir el peine, tenemos que "desperdiciar" muchos cuadrados antes, y creo que en suma no compensa respecto a duplicar el numero con cada nuevo rectangulo.
Por ejemplo, con el tema del peine, imaginar un rectangulo incial que es el peine al completo, y luego 10 rectangulos mas que "recortan" las puas, y al final, ponemos un rectangulo que corte a todas las puas en dos alturas, como si una letra E la tachamos de arriba a abajo cortandole las tres puntas. En este caso, el ultimo rectangulo crea 21 regiones a partir del peine original, PERO si os imaginais que los 10 rectangulos de las puas se ponen los ultimos, entonces cada rectangulo corto a los existentes (y no todos) en dos zona, asi que el "caso peine" es mas desfavorable que el comentado arriba.