La integral de Riemann
La integral de Riemann está basada en la llamada Medida de Jordan, y se expresa como el límite de una suma de Riemann. Vayamos por partes para entender esto.
El concepto de medida en matemáticas generaliza los conceptos habituales de longitud, área y volumen; y trata de conseguir que clases cada vez más generales de conjuntos tengan asociada una medida. Dichos conjuntos se llamarán conjuntos medibles.
Nos limitaremos al cálculo de áreas de figuras planas, si bien la extrapolación a dimensiones superiores no aporta dificultad conceptual alguna, sino merametne operativa.
La idea de la medida de Jordan consiste en atrapar la figura a medir en enlosados de rectángulos (el valor de las áreas de estos últimos son fáciles de hallar). Cuanto más fino sea el enlosado más fielmente se adaptará alas posibles anfractuosidades de la figura, de forma que es esperable que el límite del enlosado sea exactamente la medida de la figura.
A modo de test, para que dicho límite sea unívocamente determinado, se efectuarán enlosados exteriores e interiores. Los primeros cubren el conjunto de partida, y los segundos son cubiertos por él. Si el límite de las áreas por enlosados exteriores e interiores son iguales, entonces decimos que la figura es medible- Jordan, y que su medida es el valor de dichos límites coincidentes. Las sumas de los rectángulos interiores las llamaremos sumas inferiores de Riemann, y las de los extreriores sumas superiores de Riemann. Para cualquier tipo de división finita en rectángulos, la suma inferior será menor que la superior, de ahí la nomenclatura.
Es comprensible esperar que en el límite, cuando el número de rectángulos tienda a infinito porque la partición realizada en en intervalo de integración sea extremadamente fino, tanto la suma inferior como la exterior se acercarán, una por arriba y otra por abajo a la cantidad buscada. Esa es al menos la esperanza, y las funciones que así lo cumplen serán denominadas funciones Riemann-integrables.
En la mayor parte de las matemáticas que se necesitan en la física y en la ingeniería este sistema de integral es suficiente porque las figuras a tratar (planas o no) son medibles en el sentido de Jordan.
Podemos ver la idea en la siguiente imagen:
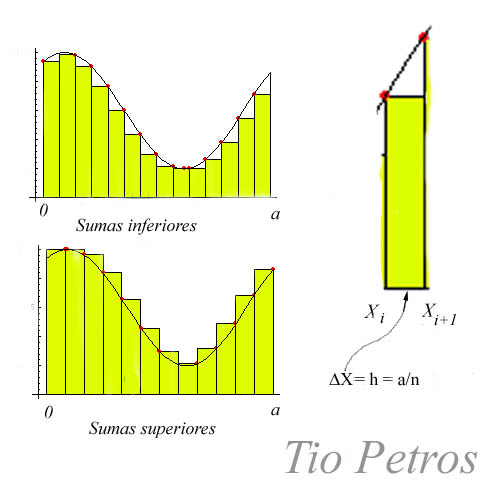
Veamos detenidamente el proceso con el cálculo de la medida bajo una parábola.
Sea la parábola f(x) = x2 .
Una partición P del intervalo cerrado [a, b] es un conjunto finito de puntos P = { x1, x1, x2, ..., xn+1} tal que:
a = x1 < x2 < x3 < ... < xn < xn+1 = b
El proceso comienza efectuando una partición de este tipo.
Fijémonos en los rectángulos interiores de la figura.
La base de todos ellos mide ΔX = a/n, cantidad que llamaremos h.
Comenzaremos hallando la La suma inferiores de f respecto de la partición P
Las alturas son función de la gráfica que queremos integrar. Dado que los estamos preocupando de los rectángulos interiores las alturas serán las correspondientes al valor más pequeño de la función entre ambos extremos (en realidad estamos interesados en el ínfimo de la función en el intervalo. En nuestro caso, y dado que la función es creciente en el intervalo considerado, el extremo a considerar será el izquierdo.
Debemos hallar los siguientes valores:
f(X1)=f(0)=0
f(x2) = f(ΔX) = f(h) = h2
f(x3) = f(2ΔX) = f(2h) = (2h)2
y por inducción:
f(xk) = f[(k-1)ΔX] = [[(k-1)h]2 = h2(k-1)2
Ahora no tenemos más que sumar las áreas de todos los rectángulos, quedando algo como esto:
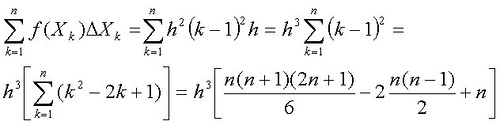
A este valor lo llamaremos suma inferior de Riemann para la función f y la partición P, I(f,p).
Ahora no tenemos más que tomar límites cuando n tiende a infinito, obteniendo el valor de la integral inferior de Riemann I*(f).
La integral inferior de Riemann no depende de la partición considerada por ser el límite cuando ésta es infinitametne fina.
Fácilmente teniendo en cuenta que h=a/n, obtenemos:
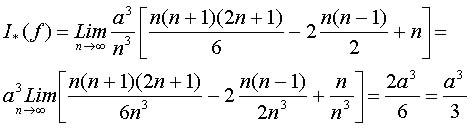
No lo haremos aquí, pero si repetimos el mismo cálculo para las suma superiores de f respecto de la partición P , que denotaremos S(f,P) y volvemos a calcular límites, obtendremos el valor I*(f), integral superior de Riemann para la función f. Obtendríamos igualmente el valor de a3/3, lo que indica que las áreas limitadas con las sumas inferiores y superiores convergen a un mismo valor, que es la llamada integral de Riemann de la función en el intervalo considerado.
Así pues, la condición de integrabilidad en el sentido de Riemann es que se de la igualdad I*(f) = I*(f)
¿Cómo serán las funciones que no cumplan esto último? Mostrar que las funciónes no Riemann-integrables aparecen incluso en sencillos problemas de probabilidad es el propósitop del próximo post. Una vez detectada la insuficiencia de la integral de Riemann, tenemos el camino abierto para generalizar el concepto y encontrar una herramienta que coincida con la de Riemann en las funciones Riemann-integrables, y que además sea válida para un mayor número de funciones.
La solución vendrá de la mano del francés Henry Lebesgue y será válida para todas las funciones que se puedan definir de manera constructiva.
Pero no adelantemos acontecimientos.
8 comentarios
Ezequiel -
yanessi -
daniel -
Roger -
rene saucedo -
rene saucedo -
Yo de nuevo -
ramon -
Un amigo me planteo un problema técnico surgido en el diseño automatizado de viviendas y dándole vueltas al asunto, derivo en una integral que en vez de tomar intervalos de x iguales, lo que llamas \"h\"(perdón por hablar con las manos). Toma intervalos de x, tales que el área de los rectángulos de las particiones es IGUAL entre sí. Después se multiplica tan ricamente.....para calcular el área total. Obviamente un poco más allá se ven todo tipo de \"fistros\" generalizados.
Y que diría TP de todo esto? ;)