De la esperanza a la integral de Lebesgue
No es que de la definición de esperanza de una variable aleatoria lleguemos al concepto de integral de Lebesgue, sino que nos apoyamos en el concepto de esperanza matemática que hemos visto varias veces en el blog, y lo utilizamos como escusa para explicar un concepto de integral que supera al tradicional de Riemann.
Hemos definido varias veces la esperanza de una variable aleatoria como la suma de los productos de los posibles valores de la misma por las probabilidades de que adopten esos valores.
Si X es una V.A. que puede tomar valores x1,...,xn con probabilidades p1,..,pn, (p1+...+pn = 1 ) entonces la esperanza de la variable X es:
E[X] = x1p1 + ... + xnpn
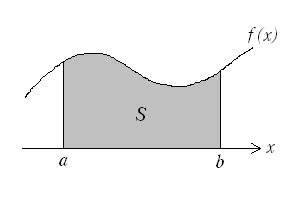
Cuando la variable es continua y toma valores en un intervalo [a,b], no podemos hablar de probabilidad de que tome un valor concreto, pues en el caso genérico, cada valor concreto tiene probabilidad nula de ocurrir (son infinitos los posibles). Hablaremos de densidad de probabilidad, entendiendo la densidad de probabilidad de un punto como el límite del cociente entre la probabilidad de un segmento que contenga a dicho punto y la longitud de dicho segmento, cuando ésta tiende a cero.
El operador esperanza se ha convertido en una integral . Sin embargo tenemos un problema: la integral habitual que se usa en ingeniería es la integral de Riemann, y se muestra absolutamente incapaz de hacer frente a problemas probabilísticos, incluso a algunos muy sencillos, como el siguiente:
¿Si escogemos un número en el intervalo [0,1] al azar cuál es la probabilidad de que el número escogido sea irracional?
La solución a este problema, casi trivial, muestra que la integral de Riemann es incapaz de afrontar contajes (pues una integral no es sino una forma de contar) en espacios abstractos como los espacios probabilísticos. Por ello hace falta una herramienta conceptual más elaborada que vendrá de la mano de Lebesgue.
Todo ello lo veremos en los próximos días. Daremos un repaso al concepto de Integral de Riemann, y veremos porqué en los casos más generales no es satisfactoria.
Hablar de integrales es hablar de maneras de contar. La combinatoria se puede definir como el arte de contar. Así lo hemos hecho en muchos posts precedentes. Sin embargo habría que hacer alguna precisión. No es lo mismo contar el número de ordenaciones de un conjunto finito de elementos que cumpla una propiedad concreta que contar los metros cuadrados que ocupa una superficie. La diferencia básica es que en el primer caso estamos en el dominio de los números enteros (o de los racionales si establecemos cocientes entre las cantidades previamente halladas), y en el segundo estamos en el dominio del continuo de los reales.
En cierto modo, estar en el dominio de R es cómodo: tenemos una serie de resultados que nos hacen agradable estar en el continuo de los reales, y que tienen que ver con temas topológicos muy profundos que ya se han discutido en el blog aquí.
Aunque es un tópico muy común, veremos que la integral de Riemann es una herramienta excelente para trabajar en "ambientes" en los que las buenas propiedades topológicas, tanto de los espacios como de las funciones a integrar, lo permiten. El problema vendrá cuando encontremos funciones, como la función de Dirichlet, que aunque definen problemas sencillos como el de encontrar la probabilidad de elegir un número racional al azar en el intervalo [0,1], no cumplen las "buenas propiedades" exigibles a las funciones para que sean integrables en el sentido de Riemann (las llamaremos funciones Riemann-integrables).
La meta será entonces encontrar una definición de integral que coincida con la de Riemann en las funciones Riemann-integrables, y que sea extensible a todas las funciones que se puedan definir de forma constructiva. Este reto es inmenso, y la forma de resoverlo me recuerda a la forma de Alejandro Magno de desatar el nudo gordiano. Para esta historia necesitaremos varios posts en los que recorreremos paisajes muy trillados y conocidos del cálculo diferencial; y otros menos conocidos y más exclusivos de la matemática menos "ingenieril".
Espero que sea un paseo agradable.
10 comentarios
eliza -
Gabriel -
Vaya si me haz ayudado a comprender mejor el tema de la entropia, pero me gustaria que analices la ultima parte
H[x]=log2N bits..
Dijiste que no es por gusto esa coincidencia.. No soy un genio en matematicas.. pero creo que se aplica en Computadoras y en la teoria de la información..
Saludos y FELICITACIONES
malambo -
Lo interesante para los comentaristas es pensar respuestas que sean también apropiadas para eventuales futuras modificaciones.
Por ejemplo tu pones: 1+1=2 y el comentarista experimentado en postes dinámicos debería contestar "es posible, pero no siempre" o "a buen entendedor, pocas cuentas" o tal vez: "la muerte, al final, siempre llega" e incluso "si p entonces p".
Sin embargo, contestaciones de este último tipo son fuertemente desaconsejadas porque al ser verdaderas siempre son válidas para cualquier blog, incluso uno de religión.
Pero vamos, no te entretengas leyendo estas elucubraciones y prosigue tu divulgación de las integrales del matemático que vivió hace tiempo.
Toni -
Gracias por divulgar las matemáticas tal y como lo haces.
Un saludo,
TioPetros -
Supongo que es un mal menor...
malambo -
samu -
Por cierto que a mi me la han explicado de muchas formas, y todas se dejan algo por el camino. A mi parecer es un asunto interesante y profundo.
PD: bueno en realidad se que terminara muy bien, y hasta yo aprendere algo, el Tio Petros siempre nos sorprende.
Jorge Alonso -
omalaled -
Saludos
malambo -