Conceptos

De la esperanza a la integral de Lebesgue

No es que de la definición de esperanza de una variable aleatoria lleguemos al concepto de integral de Lebesgue, sino que nos apoyamos en el concepto de esperanza matemática que hemos visto varias veces en el blog, y lo utilizamos como escusa para explicar un concepto de integral que supera al tradicional de Riemann.

Hemos definido varias veces la esperanza de una variable aleatoria como la suma de los productos de los posibles valores de la misma por las probabilidades de que adopten esos valores.

Si X es una V.A. que puede tomar valores x₁,...,x_n con probabilidades p₁,..,p_n, (p₁+...+p_n = 1 ) entonces la esperanza de la variable X es:

E[X] = x₁p₁ + ... + x_np_n

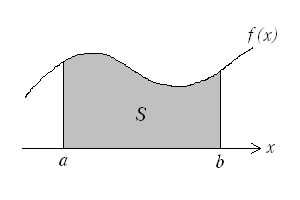
Cuando la variable es continua y toma valores en un intervalo [a,b], no podemos hablar de probabilidad de que tome un valor concreto, pues en el caso genérico, cada valor concreto tiene probabilidad nula de ocurrir (son infinitos los posibles). Hablaremos de densidad de probabilidad, entendiendo la densidad de probabilidad de un punto como el límite del cociente entre la probabilidad de un segmento que contenga a dicho punto y la longitud de dicho segmento, cuando ésta tiende a cero.

El operador esperanza se ha convertido en una integral . Sin embargo tenemos un problema: la integral habitual que se usa en ingeniería es la integral de Riemann, y se muestra absolutamente incapaz de hacer frente a problemas probabilísticos, incluso a algunos muy sencillos, como el siguiente:

¿Si escogemos un número en el intervalo [0,1] al azar cuál es la probabilidad de que el número escogido sea irracional?

La solución a este problema, casi trivial, muestra que la integral de Riemann es incapaz de afrontar contajes (pues una integral no es sino una forma de contar) en espacios abstractos como los espacios probabilísticos. Por ello hace falta una herramienta conceptual más elaborada que vendrá de la mano de Lebesgue.

Todo ello lo veremos en los próximos días. Daremos un repaso al concepto de Integral de Riemann, y veremos porqué en los casos más generales no es satisfactoria.

Hablar de integrales es hablar de maneras de contar. La combinatoria se puede definir como el arte de contar. Así lo hemos hecho en muchos posts precedentes. Sin embargo habría que hacer alguna precisión. No es lo mismo contar el número de ordenaciones de un conjunto finito de elementos que cumpla una propiedad concreta que contar los metros cuadrados que ocupa una superficie. La diferencia básica es que en el primer caso estamos en el dominio de los números enteros (o de los racionales si establecemos cocientes entre las cantidades previamente halladas), y en el segundo estamos en el dominio del continuo de los reales.

En cierto modo, estar en el dominio de R es cómodo: tenemos una serie de resultados que nos hacen agradable estar en el continuo de los reales, y que tienen que ver con temas topológicos muy profundos que ya se han discutido en el blog aquí.

Aunque es un tópico muy común, veremos que la integral de Riemann es una herramienta excelente para trabajar en "ambientes" en los que las buenas propiedades topológicas, tanto de los espacios como de las funciones a integrar, lo permiten. El problema vendrá cuando encontremos funciones, como la función de Dirichlet, que aunque definen problemas sencillos como el de encontrar la probabilidad de elegir un número racional al azar en el intervalo [0,1], no cumplen las "buenas propiedades" exigibles a las funciones para que sean integrables en el sentido de Riemann (las llamaremos funciones Riemann-integrables).

La meta será entonces encontrar una definición de integral que coincida con la de Riemann en las funciones Riemann-integrables, y que sea extensible a todas las funciones que se puedan definir de forma constructiva. Este reto es inmenso, y la forma de resoverlo me recuerda a la forma de Alejandro Magno de desatar el nudo gordiano. Para esta historia necesitaremos varios posts en los que recorreremos paisajes muy trillados y conocidos del cálculo diferencial; y otros menos conocidos y más exclusivos de la matemática menos "ingenieril".

Espero que sea un paseo agradable.

Entropía y cantidad de información (y 4)

Vamos a intentar sacarle jugo a la fórmula de la entropía de una variable aleatoria. En todo caso hablaremos de variables aleatorias discretas, que pueden tomar un número finito o al menos numerable de valores, sin embargo la extrapolación a variables continuas es muy sencilla y no añade dificultad conceptual alguna.

Primero, volvemos a poner la ilustración del post anterior, en la que se ve además el origen del concepto de entropía a partir de la cantidad de información aportada por cada posible valor de la variable aleatoria.



Puede suceder que uno de los posibles valores x_i tenga asociada una probabilidad p_i=1. Como la suma de todas las probabilidades es la unidad, eso quiere decir que los demás "posibles sucesos" tienen probabilidad cero (no son posibles, de ahí el entrecomillado anterior).

Una variable así nos está diciendo que se va a realizar el valor x_i con seguridad. A una variable aleatoria de este tipo la denominaremos degenerada , por no aportar aleatoriedad alguna.

Qué sucede con la entropía de una variable aleatoria degenerada?

Sólo tiene un valor con probabilidad mayor que cero, por lo que dicha probabilidad es uno; y para ese valor el logaritmo de la probabilidad es cero (pues log₂1=0), por lo que la entropía de dicha variable es nula.

Una v. a. nos está ofreciendo una cierta información; es como cuando el médico nos dice que tenemos un 88% de posibilidades de vencer nuestra enfermedad. No nos da tanta información como cuando nos dice con seguridad qué nos va a pasar; pero nos da más información que si nos habla de un 50% de posibilidades. La variable aleatoria degenerada no deja aleatoriedad: da la información máxima posible, y tiene entropía nula, según acabamos de ver.

Este hecho es el primer indicio de que si pensábamos que la entropía era una medida de la información que me ofrece una variable aleatoria, estábamos equivocados.

LA ENTROPIA DE UNA VARIABLE ALEATORIA NO NOS INDICA EL GRADO DE INFORMACION QUE NOS OFRECE DICHA VARIABLE

De hecho, es un muy buen indicador de lo contrario. Cuanto más baja sea la entropía de una v. a., más información nos estará dando, hasta llegar a la entropía nula en el caso de información puntual, fiel y no probabilística (en el sentido de que la ofrece con probabilidad 1)

El hecho de que hayamos dicho que la entropía era el valor esperado de la cantidad de información asociada a los valores posibles no nos debe llevar a engaño: una cosa es la información que aporta la variable aleatoria en sí, y otra es el incremento de información que nos supone el conocimiento de la materialización práctica del valor de dicha variable en un experimento. Bajo esta luz es evidente que un suceso de probabilidad uno tenga información asociada nula: ¿qué información nos va a aportar, si la variable aleatoria ya nos da toda la información posible?

Si el médico me dice que tengo una probabilidad del 100% de curarme de mi enfermedad (variable aleatoria degenerada) me aporta de principio la máxima información. Cuando me he curado (realización práctica del suceso predicho por la variable), ya no obtengo información añadida. En el extremo opuesto, si me dice que tengo un 50% de probabilidades de curación (máxima aleatoriedad) no me aporta información alguna, y mi futura curación (realización del experimento asociado a la variable aleatoria) en cambio aportará toda la información que la variable no aportaba.

La entropía de la variable es la medida esperada de la información que aportará la realización del evento asociado a la variable, no la propia variable. Por eso es que una entropía alta implica que la propia variable aporta una información pequeña. El resto de la información hasta la certeza vendrá de la materialización práctica del evento.

Vayamos a uno de los casos más sencillos de variable aleatoria: la realización de un experimento con dos posibles resultados, de probabilidad p y (1-p). El lanzamiento de una moneda (con posibles resultados 0 (cara) y 1 (cruz), o de un dado con resultados 0 (impar) ó 1 (par).

La entropía de esta variable , aplicando la fórmula de la definición es:

H[X]= -p·log₂p-(1-p)·log₂(1-p)

En el caso general tenemos infinitas distribuciones diferentes con este esquema dependiendo del valor de p, que recorre los reales en el intervalo [0,1].

Un poco de cálculo nos convencerá de que el valor máximo de la entropía es para p=0,5, y los mínimos para p=0 y p=1, para los cuales la entropía vale cero. En efecto, en ambos casos tenemos una variable degenerada; y la máxima entropía se da cuando la distribución es uniforme: todos los valores tienen la misma probabilidad de ocurrir y la variable en sí no nos aporta información alguna de cuál puede ser el que se dé en el evento.

Ahora sabemos que el máximo de entropía es para la distribución uniforme, además es muy sencillo evaluarla:

Si tenemos una v. a. X que toma valores {x₁,x₂,...,x_n} con probabilidades (p₁,p₂,...,p_n), si hay equiprobabilidad entonces p_i=1/n, para todo n, y por lo tanto:

H[X]=-(1/p)·log₂(1/p)-(1/p)·log₂(1/p)-...-(1/p)·log₂(1/p)=
log₂(p)

Esta es la mayor entropía que puede tener una variable aleatoria de n estados.

Esta fórmula:

H[X]=log₂(p)

es idéntica a la fórmula física que expresa la entropía de un sistema en función de su número de estados, salvo por la presencia de la constante de Boltzmann. Tanto en el caso físico como aquí, la elección del valor numérico de la constante depende de las unidades en las que estemos trabajando. En nuestro caso hemos elegido el asunto al dar base 2 a los logaritmos empleados y la unidad es el bit.

Así, una variable con 8 estados, si es uniformemente distribuida y por lo tanto aporta la menor información posible; tiene una entropía de H=log₂8=3 bits.

Habiendo ocho estados son precisamente 3 los bits necesarios para nombrarlos a todos (000,001,010,011,100,101,110 y 111). Esto no tiene nada de casual, sino todo lo contrario; pero es una historia que debe ser contada en otra ocasión... ocasión que deberá esperar pues este blog suspende su actividad hasta mediados-finales de Julio por motivos vacacionales.

Volveremos entonces con más energía. Que pasen un buen verano (o invierno, si nos leen desde el hemisferio sur).

Entropía y cantidad de información (3)

Supongamos que tenemos una urna con diez bolas. Sabemos que nueve son blancas y una negra. Si sacamos una bola al azar, consideremos la variable aleatoria asociada al experimento, X. La cuantificamos dándole el valor de 0 si la bola extraída es negra, y 1 si es blanca

P_{X=1} = 9/10 = 0.9

P_{X=0} = 1/10 = 0.1

Podemos hallar la esperanza de la v.a. X:

E[X]=1 · 0.9 + 0 · 0.1 = 0.9

Esto no es ninguna sorpresa: la esperanza, o valor esperado, no es sino el promedio esperado tras una multitud de repeticiones del mismo experimento. En promedio, 9 de cada 10 veces obtendremos un 1 (bola blanca), por lo que el valor promedio de la variable es precisamente 0.9

Sólo dos son los valores posibles de X , pero la información asociada a cada uno de ellos es diferente.

Recordemos la definición de cantidad de información asociada a un suceso i:



En nuestro caso, tenemos:

I₁= - log₂(0.9)= 0.15

I₀= - log₂(0.1)= 3.32

Vemos que la información asociada a sacar una bola negra (X=0) es mucho mayor que la información asociada al suceso "sacar una bola blanca". Una forma de entender esto es comprender que obtener una bola negra reduce la indeterminación completamente: sabemos que cada una de las bolas que quedan en la urna son blancas. Si hubiéramos obtenido una bola blanca, la reducción de incertidumbre es mucho menor: seguimos sin poder decir qué pasaría si hiciéramos otra extracción sin reemplazamiento de la bola previamente extraída.

Así pues, tener una variable aleatoria implica no saber el resultado que vamos a obtener, y esto implica no saber qué cantidad de información vamos a obtener al realizar el experimento, porque cada posible resultado nos aporta una cantidad de información diferente.

Esta simple idea nos sirve para definir a partir de una variable aleatoria otra variable aleatoria derivada, que consiste precisamente en la cantidad de información a obtener en el experimento. Definamos pues:

Dada una v.a. X, que toma valores {x₁,x₂,...,x_n} con probabilidades p₁,p₂,...,p_n, que aportan cantidades de información I₁,I₂,...,I_n, llamamos variable aleatoria cantidad de información asociada a X a la variable aleatoria I[X] , que toma valores I₁,I₂,...,I_n con probabilidades p₁,p₂,...,p_n.

En nuestro ejemplo, I[X] toma el valor 0.15 con probabilidad 0.9, y el valor 3.32 con probabilidad 0.1

Una propiedad importante de esta nueva variable aleatoria es que aunque deriva de la X inicial, no tiene en cuenta para nada los valores numéricos que esta X pueda adquirir: depende exclusivamente del reparto de probabilidades entre sus respectivas posibilidades.

Llegados hasta aquí, y dado que I[X] no es sino una variable aleatoria, nada nos impide preguntarnos por su valor esperado, o esperanza E[I[X]]; número que denotaremos H[X]

H[X] = E[I[X]] = 0.15 · 0.9 + 3.32 · 0.1 = 0.135 + 0.332 = 0.467

Vemos que la contribución del suceso menos probable es mayor que la del más probable, a pesar de que las cantidades de información deben estar multiplicadas por su correspondiente probabilidad.

Convenimos que un suceso de probabilidad nula no tiene ninguna relevancia en este cómputo. Es necesario este extremo porque el producto p(x)·log[P(x)] es una indeterminación cuando p(x)=0.

Qué hemos conseguido con esta definición?

Tenemos un número real, H[X], que es el valor esperado de la cantidad de información que obtendremos al obtener un resultado del experimento expresado por dicha variable aleatoria.

Este valor se denomina Entropía de Shannon de la variable dada. Y es un concepto de importancia capital en teoría de la información.

La expresión analítica de la entropía de Shannon es la siguiente:



En el siguiente post veremos qué tiene que ver esto con el desorden y porqué este concepto es importante.

Entropía y cantidad de información (2)

Cuando nos sometemos a una situación de incertidumbre es natural preguntarse qué resultado es esperable obtener. Naturalmente, esta pregunta debe ser precisada convenientemente para que tenga operatividad.

El concepto de Esperanza matemática o valor esperado habilita la herramienta idónea para responder a dicha pregunta. Si nos jugamos a cara y cruz con nuestro oponente 1 euro a una tirada, no hace falta hacer muchas consideraciones matemáticas para comprender que la esperanza del juego es nula: por simetría no podemos asignar ventaja a ninguno de los dos jugadores, por lo que ambos están igualmente expuestos a perder un euro o a ganarlo.

Cada uno de los jugadores comprende que en ausencia de trampas hay la misma probabilidad de ganar que de perder y que en cada caso, la cantidad involucrada es 1 euro. Por lo tanto este juego tiene esperanza nula; o lo que es lo mismo; es un juego que no tiene ganancia esperada. Si jugáramos un número suficientemente grande de veces, las ganancias compensarían a las pérdidas.

Cualquier juego real de apuestas tiene esperanza negativa: lo más probable es perder dinero. El motivo por el que se juega es que en caso de ganar, los premios son de escándalo. Estamos dispuestos a perder una cantidad pequeña de dinero casi con seguridad a cambio de la posibilidad, por pequeña que sea, de hacernos ricos de la noche a la mañana. Es perfectamente comprensible, de ahí que si leen ustedes en algún sitio que la mera esperanza matemática es la mejor guía ante una situación de incertidumbre, no se lo crean demasiado por ser un razonamiento demasiado simplista.

Pues bien, armados con esta idea, definimos la Esperanza matemática de una variable aleatoria X que toma valores en un conjunto { x₁ , x₂ , ... , x_n} con probabilidades p₁, p₂, ... , p_n como el número real:

E[X]= p₁· x₁ + p₂· x₂ +...+ p_n· x_n

Esto no es sino la suma de todos los posibles “premios” ponderada por la probabilidad de obtenerlos.

En el caso del juego de cara y cruz con un euro en juego, tenemos:

E[X]=0.5 · 1 – 0,5 · 1= 0

Para variables aleatorias continuas el concepto es exactamente el mismo, sustituyendo el sumatorio por una integral, y la probabilidad de cada suceso por la densidad de probabilidad. No hay ninguna diferencia conceptual y no incidiremos en ello ahora.

Antes de continuar, es bueno advertir que no toda variable aleatoria tiene una esperanza definida. Algunas tienen esperanza infinita, por ejemplo esta: Sea un juego en el que hay una probabilidad de un medio de ganar 2 euros, un cuarto de ganar 4 , un octavo de ganar 8, etc.

X toma valores en el conjunto {2ⁿ; n€N} siendo P_{{X= 2ⁿ}} = 1/2ⁿ

Seguidamente tenéis el desarrollo que demuestra que esta v. a. no tiene esperanza finita:



Visto esto, estamos en condiciones de afrontar la definición de Entropía de una variable aleatoria .

Lo haremos utilizando dos conceptos de importancia capital: el de cantidad de información visto en el post anterior y el de esperanza matemática visto ahora. Lo haremos en el próximo post, si ustedes quieren.

Entropía y cantidad de información (1).

Los niños que nacieron esta semana en el hospital materno-infantil de nuestra comarca tenían cada uno una cabeza, dos brazos y dos piernas. El sol salió por el este, se puso por el oeste y tras el ocaso el cielo se fue oscureciendo hasta volverse negro...

Noticiario imaginario

Hace cosa de un mes establecimos en este blog qué debe entenderse por variable aleatoria desde un punto de vista totalmente riguroso. Así, el concepto intuitivo de una función que puede tomar uno de entre una serie de valores con una cierta ley de probabilidad, quedaba explicado de forma bastante pormenorizada haciendo uso del concepto de espacios y funciones medibles.

Para los fines de este post, hablaremos de variables aleatorias (v.a.)de forma menos envarada. Tenemos la v.a. X, que supondremos, aunque no tiene porqué ser así, discreta. Esto quiere decir que puede tomar los valores de un conjunto finito {x₁, x₂,.., x_n}, con unas probabilidades definidas:

P{X= x₁}=p₁
P{X= x₂}=p₂
...
P{X= x_n}=p_n

Además, dado que los {x₁, x₂,.., x_n} son todos los casos posibles, tenemos que
p₁ + p₂ + ... + p_n = 1.

Nuestro propósito es definir dos conceptos relativos a las variables aleatorias: cantidad de información y entropía.

Si leen la noticia que encabeza este post (imaginaria evidentemente), verán que a pesar de su más que plausible veracidad, nunca periódico alguno publicará algo semejante. El motivo es claro: está enunciando unas noticias carentes e interés.

Conviene que analicemos un poco esa carencia de interés. En nuestro caso se debe a que los sucesos relatados son de tal habitualidad que no son dignos de ser reseñados. No se trata de que no sean importantes, o que dé lo mismo su cumplimiento que su incumplimiento. Se trata de que la importancia de una noticia es proporcional a su improbabilidad. Un notición es la reseña de un acontecimiento extraordinario que ocurre muy de vez en cuando. Si ocurre una única vez y es prácticamente irrepetible, se convierte en una primicia.

Esta idea intuitiva nos induce a hablar de la cantidad de información de un suceso. Cuanto mayor sea la probabilidad de que se produzca, menor será la información que aporta. Si el suceso es de probabilidad uno, la información que nos aporta su conocimiento es cero. En el caso límite contrario, un suceso de probabilidad cero nos aportaría una información infinita.

Precisamente la función logaritmo tiene unas propiedades muy buenas para cuantificar este extremo: log (x) vale cero para x=1, y va aumentando (en valor absoluto) hacia infinito conforme la x va desde la unidad hacia el cero. Definiremos por tanto la cantidad de información asociada a un suceso aleatorio de la siguiente manera:



El motivo del signo menos es que el logaritmo de todo número comprendido entre 0 y 1 es negativo.La elección de la base 2 para los logaritmos es de índole práctica e irrelevante para la explicación del concepto. Podríamos en principio poner cualquier base; simplemente es una cuestión de escala.

Mañana seguiremos por este camino, pero antes debemos definir qué cosa es la Esperanza matemática de una variable aleatoria . Con este concepto y el de cantidad de información bucearemos en la interpretación del concepto de entropía a la luz de la teoría de la probabilidad.

La Entropía tiene dos problemas:

1.- El concepto es algo difícil de pillar (no demasiado, pero requiere un cuartito de hora de atención)

2.- Es una palabra muy eufónica, suena tremendamente bien.

Ambas propiedades juntas hacen que muchos oradores la suelten, así sin más en medio de su discurso; como para dar empaque a su charla.

Este concepto de entropía es muy polifacético: aparece en matemáticas hablando de simples conjuntos (Entropía de Kolmogorov, de la que hablamos aquí), aparece en la teoría de la información con el aspecto que vamos a tratar en esta serie de post, y cómo no, aparece en física. Internamente subyace una unidad conceptual en todas estas versiones, como una medida del desorden de un sistema.

Seguiremos mañana definiendo la esperanza de una variable aleatoria; paso previo para definir la entropía.

Aritmética modular (5)

Quinto y penúltimo post de la serie de Lola Cárdenas sobre reglas de divisibilidad

Divisibilidad entre 4

Por tanto,

Divisibilidad entre 6

Por tanto,

Divisibilidad entre 7

Por tanto,

Notar que se repiten cíclicamente los factores por los que ir
multiplicando las cifras. Ordenando de la más baja a la más alta,
el ciclo que se da es éste: (1, 3, 2, -1, -3, -2).

Divisibilidad entre 8

Por tanto,

Divisibilidad entre 12

Por tanto,

Divisibilidad entre 13

Por tanto,

Notar que se repiten cíclicamente los factores por los que ir multiplicando las cifras. Ordenando de la más baja a la más alta, el ciclo que se da es éste: (1, -3, 9, -1, 3, -9).

Por ejemplo, 4394 es divisible entre 13. Sus cifras son: , , y . Aplicando esta regla, calculemos: , y 0 es divisible entre 13. Luego 4394 es divisible entre 13.

Aritmética modular (2)

Segundo post de Lola Cárdenas para TioPetros sobre el tema de las reglas de divisibilidad.

_______________________________________________________________________

Introducción a los criterios de divisibilidad

Cuando éramos niños, en el colegio nos explicaban las reglas de divisibilidad. Por ejemplo, nos decían que todos los números pares son múltiplos de dos, que todos los números acabados en cero o en cinco son múltiplos cinco, o que si sumamos las cifras de un número, y esta suma es múltiplo de tres, entonces el número mismo es múltiplo de tres.

La reglas de divisiblidad por dos o por cinco parecen estar bastante claras, sin embargo la regla de divisibilidad por tres ya trae consigo un modo de operar que en principio no se sabe por qué es así ni por qué funciona. ¿De dónde ha salido esa regla? Me lo pregunté tan pronto como me hicieron aprenderla en el colegio. Y lo descubrí pocos años después, "haciendo cuentas" tras una clase de álgebra, intrigada, porque sabía que ahí estaba la clave. Esas reglas salen de lo más básico de un apartado conocido como ``aritmética modular''. Y veremos al final de toda la exposición que es mucho más sencillo de lo que el nombre y lo que los primeros
conceptos sugieren.

Preliminares

Relaciones binarias

Definición

Consideremos un conjunto A. Recordemos cómo se define el producto cartesiano de un conjunto: se trata de todos los pares de la forma (a, b), donde a y b pertenecen al conjunto A. Es decir, el producto cartesiano, A x A se define como:

Llamamos pues relación binaria a cualquier subconjunto de A x A, y diremos que los pares (a, b) de dicho subconjunto están relacionados por , es decir, que (a está relacionado con b por la relación ).

Ejemplo

Si tomamos como conjunto al conjunto de los números naturales, , considerando su producto cartesiano, , podemos establecer la relación tal que relaciona a cualquier n₁ con su doble, 2n₁. Es claro que el conjunto es un subconjunto de y por tanto la relación establecida es una relación binaria.

Relaciones binarias de equivalencia

Las relaciones que nos interesan en este momento no son relaciones cualesquiera, establecidas un poco al azar, sino relaciones que cumplen tres propiedades muy interesantes:

Reflexiva: Una relación se dice reflexiva si para todo a perteneciente al conjunto A, se verifica que .
Simétrica: Una relación se dice simétrica si para todos a, b pertenecientes al conjunto A, el hecho de que implica a su vez que .
Transitiva: Una relacion se dice transitiva si para todos a, b, c pertenecientes al conjunto A, que y implica que .

Vamos a ver un ejemplo de relación binaria que sí sea de equivalencia y otra que no lo sea, para tratar de aclarar el significado de estas propiedades.

Ejemplo de relación binaria de equivalencia

Dados , decimos que si se cumple que . ¿Es de equivalencia esta relación binaria? Para contestar afirmativamente tendremos que demostrar que se cumplen las tres propiedades. Para contestar negativamente, bastará con encontrar que falla una de ellas.

Empezamos verificando la propiedad reflexiva. Sea . ¿Se cumple que ?

Por definición de la relación, esto será cierto si se cumple que . Pero dado , siempre tenemos que , luego y la relación es reflexiva.

A continuación veamos si cumple la propiedad simétrica. Sean y supongamos que . ¿Se cumplirá pues que ?

Como , por la definición de la relación se tiene que . Ahora bien, se cumplirá que si y sólo si .

Pero .

Luego y la relación es simétrica.

Por último, veamos si la relación es transitiva. Sean y supongamos que y que . ¿Se cumple que ?

Como , tenemos que , y como , tenemos que .

Se cumplirá que si y sólo si . Pero:

Por tanto y la
relación es transitiva.

Finalmente, tenemos que se cumplen las tres propiedades, y por tanto la relación binaria así definida es de equivalencia.

Ejemplo de relación binaria pero NO de equivalencia

Ahora definimos la siguiente relación: dos elementos están relacionados, si .

Veamos si cumple las tres propiedades que debe verificar para ser una relación binaria de equivalencia.

Comenzamos verificando la propiedad reflexiva. Sea , ¿se cumple que ? Esto será así si . Pero esto sólo es así si .

¿Se verifica la propiedad reflexiva entonces? No, porque para que se cumpliera, tendría que ser cierto para cualquier . Y sabemos que eso no es así. Si , entonces .

Por tanto, no se cumple la propiedad reflexiva: no tenemos que seguir examinando propiedades para afirmar que esta relación binaria no es de equivalencia.

Clases de equivalencia

Cuando tenemos una relación binaria de equivalencia sobre un conjunto , dado un elemento , definimos su clase de equivalencia como el conjunto de los elementos de que están relacionados con .

Es decir:

Dado , en tenemos pues todos los elementos de que son equivalentes a .

Pongamos un ejemplo de la vida real que, sin ser en absoluto riguroso, ayudará a aclarar este concepto.

Imaginemos que hablamos de muebles, y queremos clasificarlos. Queremos distinguir sillas de mesas, de sillones, de sofás... Así que definimos las propiedades que, indiscutiblemente, definen a una silla y la distinguen del resto de objetos. Definimos las propiedades que definene a una mesa y la distinguen del resto de objetos. Igualmente con los sillones, los sofás...

Cuando la relación permita identificar sillas entre sí pero distinguirlas de los otros tipos de muebles, etc., tendremos una relación de equivalencia. Dos elementos del conjunto "muebles" serán sillas si reunen una serie de atributos básicos. Y son sillas y no sillones porque la diferencia ha quedado perfectamente establecida, e igualmente establecidos los distintos tipos de muebles que contemplamos así como todas sus características.

Es decir, una relación de equivalencia define la manera de distinguir un tipo de elemento de otro tipo de elemento, de forma que los elementos de la misma clase de equivalencia sean, esencialmente, iguales, pero completa y distinguiblemente diferentes de los elementos de las otras clases de equivalencia: estamos formalizando el concepto de clasificación.

Conjunto cociente

Una vez tenemos todas las clases de equivalencia de según , definimos el conjunto cociente como el conjunto de todas estas clases de equivalencia. Lo expresaremos formalmente como sigue:

Notar que dados , , y que .

Aritmética modular (1)

La serie de posts que se inician con éste ha sido elaborada para TioPetros por Lola Cárdenas Luque, con quien compartimos pasión por la matemática y por el pensamiento crítico. De una manera lúdica nos irá introduciendo en los conceptos más importantes de la aritmética modular y de las reglas de divisibilidad. Les dejo con Lola, que es lo mismo que decir que les dejo en muy buenas manos.


Empecemos con el truco

Piensa un número de tres cifras. Por ejemplo, 123. Copia ese número detrás de sí mismo, para obtener con eso un número de seis cifras. A mí me queda 123123. Mi número está amañado para que me salga el truco, pero el tuyo no tiene por qué estarlo, aún no sabes qué te voy a decir que hagas con él.

Ahora divide ese número de seis cifras por 13. Yo también voy a hacerlo, y el cociente ha sido 9471. Qué curioso, la división ha salido exacta. Pues vamos a aprovecharlo. Seguro que a ti también te ha salido exacta.

Puedo verlo. Así que ahora divide ese cociente por... vamos a ver... vale, ya lo sé. Divídelo por 7.

Yo también dividiré mi 9471 por 7. Me sale 1353. Vaya, y otra vez la división exacta.

Es más, estoy convencida de que a ti también te ha salido exacta. ¿Probamos a dividir por un número más? Esta vez vamos a dividir el cociente obtenido por... hm... déjame concentrarme en tu número... Sí, ya lo veo claro. Vamos a dividir ese cociente por 11. Es más, antes de que hagas la división, te voy a decir el resultado. Te va a salir el número que has pensado al principio.

Voy a ver qué sucede con el mío. Divido 1353 entre 11 y obtengo... ¡123! ¡El número que he elegido al principio! ¿Sorprendido? Pues eso no es todo.

Ahora invierte el número de seis cifras. En mi caso quedaría 321321. Voy a decirte algo que te va a sorprender más aún: ese número que queda al invertir, también es un múltiplo exacto de 13. Y de 7. Y de 11. En este punto podría decir que he leído tu mente y he sabido, tras un rápido cálculo mental, que entre sus divisores estaban el 13, el 7 y el 11.

Es más, podría decir incluso que he intervenido en tus pensamientos para que eligieras un número de manera que, al darle la vuelta, también saliera múltiplo de 13, 7 y 11. Pero no voy a hacerlo. En lugar de eso, voy a explicarte el truco.

Cardinalidad, "tamaño", medida, dimensión (1)

____________________

Es increíble que un concepto que en la vida real sea tan simple de entender como el concepto de “tamaño” sea tan difícil de aprehender desde la matemática.

En una primera aproximación, si hablamos de conjuntos parece que entre dos de ellos es fácil decidir cuál es más grande: no hay más que establecer una correspondencia biyectiva entre ambos, o al menos intentarlo. Si lo conseguimos, habremos conseguido emparejar a cada elemento del primer conjunto con uno y sólo un elemento del segundo, por lo tanto ambos conjuntos tendrán el mismo número de elementos. Lo bueno de este método es que no hace falta construir efectivamente la biyección uno a uno , sino que basta con demostrar que existe.

No obstante, aquí se acaban las buenas noticias. La idea anterior nos da un buen criterio de igualdad de tamaño en cuanto a cardinalidad, o a número de elementos entre dos conjuntos. Dado que un conjunto no es sino eso: una colección de elementos, uno podría preguntarse qué más queremos.

Pues queremos bastante más. La cardinalidad es una buena idea para medir conjuntos finitos: un conjunto de 1000 elementos es mayor que uno de 999 elementos; pero entre dos conjuntos de infinitos elementos la cosa es más complicada: ¿dos conjuntos infinitos de la misma cardinalidad tienen el mismo tamaño?

El lector debiera darse cuenta de que estoy haciendo trampa con la pregunta anterior. Estoy preguntando por el tamaño de dos conjuntos como si el concepto estuviera aclarado, y no lo está. La existencia del concepto tamaño parece llevar consigo la existencia de una relación de orden entre conjuntos, de manera que podamos decir que uno que otro o si ambos son del mismo tamaño .

Podemos demostrar que la cardinalidad no es una buena idea para comparar tamaños por la simple existencia de conjuntos de igual cardinalidad y “tamaños” diferentes.

Consideremos los intervalos [0,1] y [0,2]. Ambos tienen la misma cardinalidad, la del continuo. En efecto, es muy sencillo emparejar cada elemento de [0,1] con uno y sólo uno de los elementos de [0,2], simplemente haciéndolo corresponder con su doble. Así de sencillo. Si no nos sorprende es por que lo sabemos desde niños, no porque no sea sorprendente.

Así pues, tenemos una nueva manera de comparar “tamaños” entre conjuntos cuando la cardinalidad no es buena guía: la medida de lebesgue de los mismos.

Cuando hablábamos de variables aleatorias definimos la medida de Lebesgue: en el seno de una sigma-álgebra, y dijimos que la medida de un intervalo [a,b], ó (a,b) ó (a,b] ó [a,b) es el número real m=b-a.

Ahora se ve que desde esta perspectiva los intervalos [0,2] y [0,1] son de medida diferente, a pesar de tener la misma cardinalidad. Uno es el doble del otro más concretamente.

Como un punto p equivale al intervalo [p,p], queda claro que la medida de cualquier punto es m = p-p = 0.

Cualquier conjunto finito de puntos tendrá asimismo medida nula. Es más, cualquier conjunto numerable de puntos la tendrá nula también, pues por propiedad de las sigma-álgebras, la medida de una unión numerable es la suma de las medidas, y una suma numerable de ceros es cero.

Así pasaba con el conjunto Q, que tratamos cuando hablábamos de la insoportable levedad del conjunto Q; era denso en R , y exhibía una curiosa propiedad que parecía (falsamente) hacerlo igual de grande que todo R: entre dos puntos de Q siempre había uno de R ( en realidad infinitos). Pero también era cierto lo contrario: entre dos puntos de R siempre había infinitos de Q.

A pesar de este quid procuo , veíamos que Q no era sino polvo fractal dentro de R, y que su medida era cero. Q era ubícuo en R, pero era numerable (otra sorpresa dilucidada por Cantor y muchas veces comentada aquí), y medía excatamente cero.

Lo que no está nada claro es qué ocurre cuando el conjunto es una unión no numerable de puntos. Dado que un intervalo es precisamente eso, y que tiene medida no nula, sabemos que ciertos conjuntos infinitos (respecto a su cardinalidad) no numerables son de medida no nula. ¿Pero lo serán todos?

La intuición nos indica que así es.

Sin embargo, la intuición es tan mala consejera en matemáticas...

Seguiremos en el próximo post mostrándoles un conjunto con cardinalidad infinita no numerable que, a pesar de ello tiene medida cero, el conjunto de Cantor . Lo cual nos hará ver que la relación entre medida y cardinalidad es complicada, y que debemos abandonar para siempre la idea preconcebida de que podíamos imaginar un concepto de “tamaño” que fuera siempre satisfactorio para comparar varios conjuntos.

Se mezclarán en este nuevo paseo otros conceptos importantísimos como el de dimensión .

Pero no adelantemos acontecimientos.

Atrapando el concepto de azar (5)

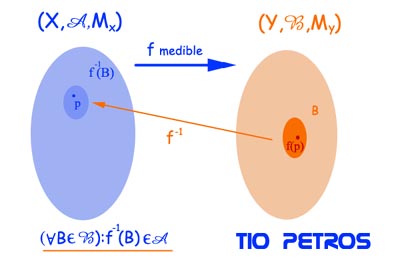A lo largo de estos tres posts repasamos hace unos meses el concepto de continuidad en espacios generales. Decíamos allí que la continuidad de una función entre dos espacios topológicos era una propiedad relativa, no absoluta de la función.

Unas topologías harían continua una determinada función y otras no. La noción de proximidad surgía de la topología sin necesidad de tener una métrica o forma de medir distancias definida, y decíamos que:

Una función continua en un punto p transforma puntos próximos a p en puntos próximos a f(p), y esa proximidad se establece en virtud de los entornos de las respectivas topologías.

Otra forma de decirlo es que la función, para ser continua debe "ser respetuosa" con las topologías de partida y de llegada.

El concepto de función continua y de función medible es radicalmente diferente, pero operativamente análogo.

En el caso que nos ocupa, no tenemos espacios topológicos, sino espacios de medida , que como hemos dicho son una tríada (X,A,M), donde X es un conjunto cualquiera, A es una sigma-álgebra subre X y M es una medida definida en A.

Supongamos que tenemos dos espacios de medida: (X,A,M_X) y (Y,B,M_Y); y una aplicación f de X a Y. Diremos que f es una función medible cuando la antiimagen de todo subconjunto de Y que sea elemento de B es un subconjunto de X que es a su vez elemento de A.

De esta forma, la función “es respetuosa” con las sigma-álgebras de partida y de llegada.

Este aparente galimatías esconde una idea extremadamente sencilla: los elementos de las respectivas sigma-álgebras son simplemente aquellos subconjuntos para los cuales tiene sentido aplicar el concepto de medida, y por ello se denominan conjuntos medibles . La propiedad pedida a las funciones medibles exige que cada medible del conjunto de llegada tenga un alter ego medible en el conjunto de partida del cual es imagen por dicha aplicación.

Es fácil comprender que este tipo de funciones son las interesantes entre espacios medibles.

Las variables aleatorias que aún estamos por definir son aplicaciones medibles entre dos espacios de medida: el origen es un espacio probabilístico (X,A,P), donde P es una medida definida en X tal que P(X)=1, y por lo tanto es una probabilidad. Y el de llegada es en conjunto de números reales R.

Lo único que nos falta es dotar a R de una sigma-álgebra para tener el panorama completo. Y eso es muy fácil de hacer: la medida en R será la extrapolación de la noción intuitiva de longitud a todos los conjuntos medibles de R. Esta medida se denomina medida de Lebesgue . Definir la medida de Lebesgue es dar una pauta para encontrar la medida de cualquier subconjunto medible de R. Como cualquiera de tales elementos debe poder ser obtenido por uniones y pasos a complementario de elementos, en virtud de la definición de sigma-álgebra, definiremos tales elementos primitivos como los intervalos [a,b], y definiremos su longitud como el número real l[a,b]=b-a.

Las propiedad sigma-aditividad de la medida junto con las propiedades generales de toda sigma-álgebra nos facilita definir la medida de cualquier subconjunto que pertenezca a esta sigma-álgebra generada por los intervalos de la recta real. Recibe el nombre de sigma-álgebra de Borel , y sus elementos se denominan borelianos .

Es mucho más fácil encontrar borelianos en la recta que no borelianos. Cualquier cosa incluida en Rque se imaginen (a no ser que sepan mucho o tengan mucha imaginación) es un boreliano. Los intervalos lo son, sean abiertos o cerrados (radical diferencia con las topologías),los puntos aislados lo son también... efectivamente, por uniones, intersecciones finitas o infinitas numerables, y con pasos a complementario (operaciones permitidas en las sigma-álgebras) lo podemos conseguir casi todo.

Es ese casi el que complica tanto la teoría de la medida: existen como anunciábamos ciertos subconjuntos de R tan endiablados que no son borelianos, y para ellos no se puede definir medida alguna. Estos elementos son los que posibilitan en R³ cosas tan inexplicables como la paradoja de Tarski-Banach , de la que hablamos en su día aquí.

Tenemos la estructura montada. En el próximo post veremos la definición rigurosa de variable aleatoria y comprenderemos mejor esa idea intuitiva de que una variable aleatoria es una variable que toma valores en función del azar. Entonces comprobaremos que no es una ocurrencia pedir que sea una función medible, sino que esta propiedad es la que nos posibilitará a inducir una probabilidad en R.

Seguiremos dentro de unos días.

Atrapando el concepto de azar (4)

Azar es una palabra vacía de sentido, nada puede existir sin causa.

Voltaire

FUNCIONES DE CONJUNTO. MEDIDAS DE CONJUNTO

Siguiendo el guión que nos hemos trazado en posts anteriores, pasamos a definir las funciones de conjunto, necesarias para explicar cómo se define una probablidad en un conjunto de sucesos.

Como hemos avanzado, una función de conjunto es el concepto riguroso de una idea intuitiva muy sencilla: una regla que asigna a cada conjunto de una colección determinada un número real. Esta definición intuitIva se formaliza mediante dos propiedades que debe cumplir tal “regla” para que merezca el nombre de función de conjunto.

1.- Al conjunto vacío le debe corresponder el cero

2.- Si tenemos una suma finita de conjuntos pertenecientes al campo de definición de la función, todos ellos disconjuntos dos a dos, entonces la medida de la unión de todos ellos será igual a la suma de las medidas individuales. Diremos que las medidas de conjuntos deben ser aditivas

Si esta propiedad 2 se hace extensiva a colecciones numerables de conjuntos, entonces la función se denomina sigma-aditiva.

Es del todo evidente que estas definiciones deben su razón de existencia a las propiedades intuitivas que todos tenemos en mente cuando hablamos de “medidas”. Pensémos en triángulos, cuadrados y polígonos generales en un plano. Pensémos en ellos no como figuras geométricas, sino como subconjuntos de un conjunto más general (el plano). A cada subconjunto le asociamos una “medida” de su área, que cumple evidentemente las propiedades pedidas. En efecto, la aditividad es una propiedad incuestionable que debe cumplir toda medida de conjunto para que responda a la idea previa que todos tenemos de lo que es una medida. Viene a ser algo así como un teorema de conservación del área generalizado a medidas más generales que la del área: si descomponemos una figura en n trozos disjuntos, la medida del original coincide con la medida de las partes.

La propiedad 3 engloba a la 2, y es la propiedad ad hoc para las sigma-álgebras, ya que por su propia definición (ver post anterior) tenemos asegurada la pertenencia de la suma infinita a dicha sigma-álgebra.

Para que la función de conjunto sigma-aditiva sea una medida ya sólo necesitamos una cosa: que todo conjunto tenga una medida no negativa.

Y para que dicha medida sea una probabilidad, lo único que hace falta es que la medida del conjunto completo sea la unidad. Ahora se ve que la probabilidad nace de la teoría de la medida sin duda alguna. Sin embargo la teoría de la probabilidad no es un mero apartado de la teoría de la medida; sino que tiene sabor propio, debido a conceptos como independencia , que en teoría de la medida no existen.

Recapitulemos: en Teoría de la probabilidad tenemos un conjunto X de sucesos elementales, más una colección de subconjuntos suyos, llamados simplemente sucesos o eventos. La estructura de dicha colección es la de una sigma-álgebra. Además, tenemos definida una probabilidad en dicha sigma-álgebra. Esto quiere decir que cada elemento de la colección de subconjuntos tiene asociado un valor comprendido entre 0 y 1. Todo ello junto forma un espacio probabilístico.

Es decir un espacio probabilístico es la terna (X, A, P), donde X es un conjunto cualquiera, A una sigma-álgebra suya y P una medida de probabilidad definida en A.

Aquí habitan las variables aleatorias , de cuya definición estamos ya cerca.

Antes de seguir convendría aclarar dos cosas:

1.- La propiedad primera de las medidas no es necesaria, ya que puede deducirse de la segunda. ¿Sabría el lector hacerlo?

2.- Aún no hemos respondido a una pregunta muy irritante: hemos visto que las sigma-álgebras cumplen por su propia constitución las propiedades “guays” para construir un espacio probabilístico, pero ¿No podríamos haber contemplado simplemente el conjunto de partes de X como conjunto de sucesos? Al fin y al cabo, al ser el mayor conjunto posible, cumple trivialmente las propiedades necesarias, y es infinitamente más sencillo de definir...

La respuesta de la pregunta 1 la dejo en el aire hasta el próximo post; es muy sencilla. La respuesta a la pregunta 2 es sin embargo una de las mayores sorpresas que uno se lleva al estudiar matemáticas. Personalmente dos cuestiones matemáticas , por su antiintuitividad me sorprendieron enormemente cuando las estudié. Una es el hecho de que el conjunto Q de los racionales sea numerable, y otra es esta: No a todo subconjunto de un conjunto general se le puede aplicar una medida .

Esto quiere decir que incluso en un conjunto tan poco inamistoso como el intervalo [0,1] ; de longitud unidad; existen subconjuntos que no tienen una longitud asociada. Que no se lleve el lector a engaño; no tener medida asociada NO es tener medida cero; es exactamente eso: no tenerla en absoluto.

La demostración de esto es un poco complicada, y hace uso del axioma de elección . Consiste en construir efectivamente un subconjunto de [0,1] para el cual no podemos asociar ninguna longitud sin caer en contradicción.

Es por eso que el sistema de subconjuntos en los que se define la probabilidad debe ser una sigma-álgebra, menos fina que el conjunto de partes de X.

Seguimos mañana.

Si ustedes quieren.

Atrapando el concepto de azar (4)

Azar es una palabra vacía de sentido, nada puede existir sin causa.

Voltaire

FUNCIONES DE CONJUNTO. MEDIDAS DE CONJUNTO

Siguiendo el guión que nos hemos trazado en posts anteriores, pasamos a definir las funciones de conjunto, necesarias para explicar cómo se define una probablidad en un conjunto de sucesos.

Como hemos avanzado, una función de conjunto es el concepto riguroso de una idea intuitiva muy sencilla: una regla que asigna a cada conjunto de una colección determinada un número real. Esta definición intuitIva se formaliza mediante dos propiedades que debe cumplir tal “regla” para que merezca el nombre de función de conjunto.

1.- Al conjunto vacío le debe corresponder el cero

2.- Si tenemos una suma finita de conjuntos pertenecientes al campo de definición de la función, todos ellos disconjuntos dos a dos, entonces la medida de la unión de todos ellos será igual a la suma de las medidas individuales. Diremos que las medidas de conjuntos deben ser aditivas

Si esta propiedad 2 se hace extensiva a colecciones numerables de conjuntos, entonces la función se denomina sigma-aditiva.

Es del todo evidente que estas definiciones deben su razón de existencia a las propiedades intuitivas que todos tenemos en mente cuando hablamos de “medidas”. Pensémos en triángulos, cuadrados y polígonos generales en un plano. Pensémos en ellos no como figuras geométricas, sino como subconjuntos de un conjunto más general (el plano). A cada subconjunto le asociamos una “medida” de su área, que cumple evidentemente las propiedades pedidas. En efecto, la aditividad es una propiedad incuestionable que debe cumplir toda medida de conjunto para que responda a la idea previa que todos tenemos de lo que es una medida. Viene a ser algo así como un teorema de conservación del área generalizado a medidas más generales que la del área: si descomponemos una figura en n trozos disjuntos, la medida del original coincide con la medida de las partes.

La propiedad 3 engloba a la 2, y es la propiedad ad hoc para las sigma-álgebras, ya que por su propia definición (ver post anterior) tenemos asegurada la pertenencia de la suma infinita a dicha sigma-álgebra.

Para que la función de conjunto sigma-aditiva sea una medida ya sólo necesitamos una cosa: que todo conjunto tenga una medida no negativa.

Y para que dicha medida sea una probabilidad, lo único que hace falta es que la medida del conjunto completo sea la unidad. Ahora se ve que la probabilidad nace de la teoría de la medida sin duda alguna. Sin embargo la teoría de la probabilidad no es un mero apartado de la teoría de la medida; sino que tiene sabor propio, debido a conceptos como independencia , que en teoría de la medida no existen.

Recapitulemos: en Teoría de la probabilidad tenemos un conjunto X de sucesos elementales, más una colección de subconjuntos suyos, llamados simplemente sucesos o eventos. La estructura de dicha colección es la de una sigma-álgebra. Además, tenemos definida una probabilidad en dicha sigma-álgebra. Esto quiere decir que cada elemento de la colección de subconjuntos tiene asociado un valor comprendido entre 0 y 1. Todo ello junto forma un espacio probabilístico.

Es decir un espacio probabilístico es la terna (X, A, P), donde X es un conjunto cualquiera, A una sigma-álgebra suya y P una medida de probabilidad definida en A.

Aquí habitan las variables aleatorias , de cuya definición estamos ya cerca.

Antes de seguir convendría aclarar dos cosas:

1.- La propiedad primera de las medidas no es necesaria, ya que puede deducirse de la segunda. ¿Sabría el lector hacerlo?

2.- Aún no hemos respondido a una pregunta muy irritante: hemos visto que las sigma-álgebras cumplen por su propia constitución las propiedades “guays” para construir un espacio probabilístico, pero ¿No podríamos haber contemplado simplemente el conjunto de partes de X como conjunto de sucesos? Al fin y al cabo, al ser el mayor conjunto posible, cumple trivialmente las propiedades necesarias, y es infinitamente más sencillo de definir...

La respuesta de la pregunta 1 la dejo en el aire hasta el próximo post; es muy sencilla. La respuesta a la pregunta 2 es sin embargo una de las mayores sorpresas que uno se lleva al estudiar matemáticas. Personalmente dos cuestiones matemáticas , por su antiintuitividad me sorprendieron enormemente cuando las estudié. Una es el hecho de que el conjunto Q de los racionales sea numerable, y otra es esta: No a todo subconjunto de un conjunto general se le puede aplicar una medida .

Esto quiere decir que incluso en un conjunto tan poco inamistoso como el intervalo [0,1] ; de longitud unidad; existen subconjuntos que no tienen una longitud asociada. Que no se lleve el lector a engaño; no tener medida asociada NO es tener medida cero; es exactamente eso: no tenerla en absoluto.

La demostración de esto es un poco complicada, y hace uso del axioma de elección . Consiste en construir efectivamente un subconjunto de [0,1] para el cual no podemos asociar ninguna longitud sin caer en contradicción.

Es por eso que el sistema de subconjuntos en los que se define la probabilidad debe ser una sigma-álgebra, menos fina que el conjunto de partes de X.

Seguimos mañana.

Si ustedes quieren.

Atrapando el concepto de azar (1)

En matemáticas las cosas están claras. Me explico: no hay ninguna indefinición en los conceptos, y las definiciones son claras, precisas y exentas de ambigüedad. Lo que ocurre es que, a veces, la sutileza de los conceptos a emplear exige una aparentemente complicada terminología.

Así ocurre con la definición de variable aleatoria . En una primera aproximación, la expresión variable aleatoria parece remitir a una variable que toma valores en función del azar. Esa primera impresión es totalmente correcta; pero fijar el concepto con el rigor que se exige en matemáticas no es tarea trivial. El presente post tiene la misión de acercar al lector a una definición algo más precisa de esto último.

La primera complicación viene del mundo en el que habitan las variables aleatorias, más complicado de explicar que el mundo de las variables habituales del cálculo infinitesimal.

En el cálculo infinitesimal, una función de n variables f(x,y,z,...t) “habita” en el espacio n-dimensional formado por las variables x,y,z,..,t. Este universo por muy n-dimensional que pueda ser es muy parecido al que habitamos nosotros: se tratá de un espacio métrico en el que existen distancias entre puntos. La propia función consiste en una aplicación que a cada punto del dominio de la función le hace corresponder un número, real o complejo.

Las de variable aleatorias no habitan en espacios métricos de este tipo, y esta es una diferencia radical. Su espacio natural es un espacio probabilístico, así que empezaremos por el principio.

La primera diferencia radical entre un espacio probabilístico y un espacio habitual (un espacio métrico n-dimensional) es que el segundo está formado por “puntos”; mientras que el primero está formado un conjunto en la acepción más general de la palabra, junto con sus elementos y subconjuntos; más una probabilidad definida en su seno . La frase anterior está en cursiva para resaltar el hecho de que tenemos mucho por definir antes de poder hablar alegremente de una probabilidad definida en el seno de un conjunto.

Así pues, una variable aleatoria no hará corresponder un valor concreto a cada punto de un espacio, sino que tendremos un conjunto de partida, que llamaremos X, y la de variable aleatoria hará corresponder valores concretos elementos concretos de dicho conjunto original.

He subrayado valores concretos para hacer hincapié en el hecho de que la aleatoriedad no reside en la atribución del valor a cada subconjunto. Repito: a cada elemento en el cual la variable aleatoria esté definida, la variable aleatoria le hace corresponder un número real (o complejo) fijo.

Dónde reside entonces la aleatoriedad?

Pues en el propio espacio de definición, que por eso se denomina espacio probabilístico. Para definir qué cosa es un espacio probabilístico, es necesario tener unos conceptos previos, lo que me da pié a iniciar una serie de posts sobre el tema

Haremos una incursión cualitativa en la teoría de la medida, en los espacios medibles y por lo tanto en las álgebras de conjuntos y sigma-álgebras. Espero que les guste el paseo.

Cuádrame esta lúnula.

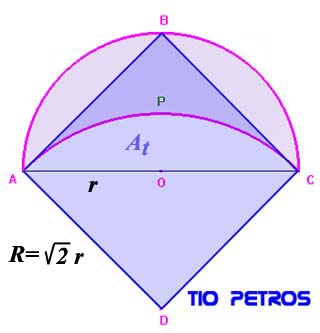En una ocasión, hablamos de los ingenuos trisectores de ángulos.

Llamábamos así a estas personas empeñadas en demostrar lo imposible. Existe una fauna muy variada de personajes de este pelo; en cuestiones físicas se agolpan alrededor del mito de la máquina de movimiento continuo, y en matemáticas alrededor de tres problemas imposibles: la duplicación del cubo, la trisección de un ángulo cualquiera y la cuadratura del círculo .

Decíamos entonces que la imposibilidad de estas tres construcciones se debe a resultados que provienen de la teoría de Galois, y que se resumen en dos proposiciones, ambas perfectamente consolidadas, demostradas y admitidas por la comunidad matemática desde hace muchísimo tiempo:

1.- Todos los números de Q son construibles.

2.- Un número real es construible si y solo si es solución de una ecuación de grado potencia de dos en Q
La cuadratura del círculo implica al número pi, que no es solución de ningún polinomio en Q, la duplicación del cubo implica la construcción de la raíz cúbica de dos, que es solución de un polinomio de grado tres (no es potencia de dos), y la trisección del ángulo de 60º implica la construcción de otro número solución de una ecuación de grado tres, y por lo tanto las tres son imposibles. Pueden existir métodos para trisecar un ángulo concreto (el del ángulo recto es trivial), pero nunca, NUNCA el de 60º.

Sucede que existen ciertos problemas parecidos en apariencia a los tres anteriores, que sí son posibles, y vamos a ocuparnos de uno de ellos: la cuadratura de la lúnula de Hipócrates .

Una lúnula es la porción de plano comprendida entre dos arcos de circunferencia. En la figura tienen una lúnula de Hipócrates , que es una lúnuna con las proporciones dadas por las dimensiones de un cuadrado ABDC. Uno de los dos arcos es el ABC, con centro en 0 y radio r = OA. El otro es el APC, con centro en D y radio R = AD.

El área de la lúnula es la diferencia entre el semicírculo de centro en O y radio OA y el sector circular APC

Llamemos A_L al área de la lúnula; A_s al área del semicírculo y A_t al área del sector antes citados.

Tenemos A_L = A_s - A_t
Y desarrollando podemos escribir:



Así pues, el área de la lúnula es r ², y como r ²=R²/2, tenemos que el área de la lúnula es la mitad del área del cuadrado ABCD, o lo que es lo mismo: es igual al área del triángulo ABC, todo ello perfectamente construible con regla y compás a partir de la lúnula.

¿A que es sorprendente un área de una figura limitada por arcos de circunferencias en la que no aparece pi?

Y es que la resta de dos números irracionales ( o en este caso lo que es aún peor: transcendentes) bien puede ser un número racional.

En el fondo no hay misterio alguno: la explicación radica en la igualdad de dos áreas: el área A_s del semicírculo ABC, y el área del cuadrante de círculo de centro en D y radio R. Llamemos X a dicho área.

El área de la lúnula es igual a la diferencia entre A_s y A_t. La primera vale X y la segunda vale (X -Q) siendo Q el área del triángulo ADC.

Por ello, el área buscada vale

A_L = X - (X -Q) = Q.

Tanto (X -Q) como X son trascendentes, no así Q, que es un número bien racional.

Mirar y ver

Otra muestra de la capacidad divulgativa del desaparecido Miguel de Guzmán ha sido publicada en España, una vez más por la editorial nivola. Se trata de Mirar y ver .

En realidad no es ninguna novedad editorial; se trata de una colección de ensayos que fue publicada en 1.976 por la editorial Alambra, y reeditada por el equipo de la OMA (Olimpiada Matemática Argentina) años después. Sin embargo, es una buena noticia que se vuelva a ver por las librerías esta preciosidad de ensayos de geometría intuitiva, como los llama su autor. La edición es de marzo del 2.004.

Se trata de un librito de poco más de 100 páginas, con unas gráficas extremadamente claras y unas explicaciones rigurosas y sencillas. Se nota la mano del autor desde el primer párrafo.

Los capítulos son los siguientes:

Introducción
Las matemáticas de una cuadrícula
Los siete puentes de Königsberg
De una sola estocada
Rompiendo figuras
La iluminación más barata
Cuatro desigualdades fecundas
El arte de mirar correctamente
Triangulando el polígono
Dadme un punto fijo
Apéndice
Bibliografía

Pese a su aspecto ligero y claro, no es un libro que pueda leerse sin gran atención, pero el resultado del esfuerzo bien vale la pena.

Según se puede leer en la propia contraportada, La elección de los temas ha sido guiada por el deseo de presentar objetos matemáticos que tuviesen profundidad y belleza y que, al tiempo, representasen líneas de pensamiento actuales.

Ficha:
MIRAR Y VER
Miguel de Guzmán
Editorial Nivola
Colección El rompecabezas, nº 8
ISBN: 85-95599-46-5
Encuadernación: Rústica, con solapas
128 páginas

Precio: 9,90 €. (4% IVA incluido)

La conjetura de Borsuk

Dos reflexiones pueden servir para empezar este post, y ambas han sido realizadas bastantes veces desde este blog. La primera es que las conjeturas tienen en matemáticas un valor muy exiguo como afirmaciones, y un gran valor como acicate para nuevas investigaciones. De hecho, un sinnúmero de veces resultan ser falsas. Sin embargo el reto de demostrarlo ha espoleado a investigadores para transitar por caminos poco conocidos, alumbrando de paso rincones de la matemática, cuando no descubriendo zonas totalmente nuevas, más importantes que la mera dilucidación de la verdad o falsedad de la afirmación de la conjetura.

La segunda es que en matemáticas no hay nada inocente. La propiedad más ingenua en apariencia, el teorema más tonto, la propiedad más aparentemente infantil puede dar pie a complicaciones de extraordinario calado, y generalizaciones inimaginables a priori.

Hoy pretendo hablarles de algo bastante poco conocido: la conjetura de Borsuk .

El inicio del asunto no puede ser más simple: dado un subconjunto de R ² , como el F de la figura, definimos el diámetro del mismo como el menor número real que es más grande que la distancia de dos puntos cualesquiera de F . En la figura, el diámetro de F es igual a la distancia entre los puntos A y B, los más alejados de entre todas las parejas de puntos de F .

Les muestro una partición de F en dos subconjuntos, F₁ y F₂ . Los diámetros respectivos de cada uno de ellos son menores que el diámetro del conjunto F original.

Normal , pensarán. Pues no, no es tan normal. Si nuestro conjunto de partida F es una figura tan poco rebuscada como un triángulo equilátero, entonces no podemos partirlo en dos figuras que tengan ambas menor diámetro que el original. El motivo es claro: al repartirse tres vértices entre dos, alguno se quedará con dos de ellos. Para ese, el diámetro será necesariamente igual al del objeto original. En resumen: necesitamos dividir el triángulo en tres partes para obtener diámetros menores que el original en cada una de las figuras de la partición.

Pueden ver la partición necesaria en la siguiente figura:



Así pues, las cosas no son tan sencillas. Llamemos B(F) al número entero que representa la mínima cantidad de trozos necesarios para partir la figura F de forma que todos los trozos sean de menor diámetro que el original.

¿Cuánto puede valer B(F) para una figura plana general? ¿Y para una figura tridimensional? ¿Y si F tiene 27.389 dimensiones?

Como pueden ver, la cosa se complica.

Para el caso de dos dimensiones, Borsuk demostró en 1.933 que con las tres divisiones que necesitaba el triángulo equilátero bastaba para cualquier figura. Así pues B(F) era menor o igual a 3 para cualquier figura de dos dimensiones.

Esto le dió pié a presentar su conjetura para el caso más general, que dice:

Sea F un subconjunto acotado del espacio n-dimensional. Entonces B(F) es menor o igual a (n+1).

Era una conjetura arriesgada. Conjeturar el caso general cuando sólo se conoce un caso concreto me recuerda a hablar de la posibilidad de vida extraterrestres cuando sólo conocemos el cao de nuestro planeta. Es tema harto difícil.

Sin embargo, el caso para tres dimensiones cayó en 1.955 ( veintidos años después del reto de Borsuk), cuando Eggleston demostró que para tres dimensiones hacían falta a lo sumo... ¡cuatro divisiones!. La conjetura cobraba fuerza.

La demostración de Eggleston debe ser de una complejidad inusitada, pero válida. Dos años después otro matemático, Grunbaum dió otra demostración del mismo hecho, algo más sencilla pero igualmente endiablada.

Quedaba aún el caso general... que vino a demostrar que la conjetura era falsa. Lo vemos en breve, si ustedes quieren; como siempre.

Polinomios ciclotómicos

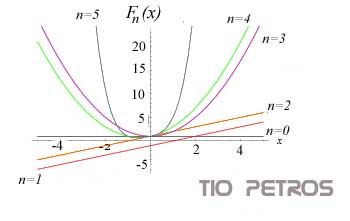Hemos explicado en post recientes que las raíces de la unidad se distribuyen a lo largo de la circunferencia unidad en el plano complejo, dividiéndola en n partes iguales. Vimos que cada uno de los valores de la raíz n-ésima de la unidad se podía expresar mediante el número complejo e^i(2PI/n)k. Dando valores a k desde 1 hasta n obtenemos todas las raíces. No lo dijimos en su momento, pero a dichos números complejos unitarios se les denomina números de Moivre .

Estas raíces son las soluciones de la ecuación polinómica :

xⁿ=1

Pues bien, a aquellos polígonos irreducibles cuyas raíces son raíces de la unidad se llaman Polinomios ciclotómicos . Esta bella palabra significa etimológicamente “que corta a la circunferencia”; como podemos ver tienen el nombre muy bien puesto. No son ellos quienes cortan a la circunferencia en R ², sino sus raíces en el plano complejo.

Nuestro polinomio genérico xⁿ-1 no será ciclotómico para todo valor de n. De hecho lo será sólo para n=1. El motivo es que en la propia definición de Polinomio ciclotómico se expresa que dicho polinomio debe ser irreducible.

Los polinomios son expresiones en forma de suma de potencias de ciertas variables, denominadas indeterminadas . Consideraremos únicamente polinomios racionales de una indeterminada. Su forma genérica es:

P(x)=a_nxⁿ+a_n-1x^n-1+ a_n-2x^n-2+...+ a₁x+a₀

Los números a_n son los coeficientes; que pertenecerán al cuerpo de los racionales.
Pues bien; el conjunto de todos los polinomios con la operación suma y producto habituales resulta ser un anillo, que llamaremos Z[x] o Q[x], para el caso de que los coeficientes sean enteros o racionales.
Z[x] o Q[x] resultan ser anillos y no cuerpos, y la relación de divisibilidad entre los polinomios se define al uso:

Diremos que un polinomio P(x) divide a otro Q(x) cuando existe un tercero
Z(x) tal que Q(x)=Z(x)·P(x)

Diremos que un polinomio es irreducible cuando no puede expresarse como producto de otros dos. Por lo tanto, obtendremos los sucesivos polinomios ciclotómicos factorizando los polinomios genéricos xⁿ=1.

El primero de ellos provendrá de la ecuación x=1; y por lo tanto es
F₁(x)=x-1.

Para n=2, tenemos x²=1, que en forma de polinomio es x²-1 Ahora bien; este polinomio se puede expresar como (x+1)·(x-1). Como el segundo factor era el primer polinomio ciclotómico, el otro es nuestro segundo:
F₂(x)=x+1.

Si continuamos, para n=3 tenemos que el polinomio x³-1 es divisible por (x-1), pudiendo ser factorizado así: x³-1=(x-1)·(x²+x+1)

Este último factor es por tanto el tercer polinomio ciclotómico:

P₃(x)= x²+x+1

Esa es la pauta para la obtención de los sucesivos polinomios ciclotómicos

· F₁(x) = x-1
· F₂(x) = x+1
· F₃(x) = x²+x+1
· F₄(x) = x²+1
· F₅(x) = x⁴+x³+x²+x+1
· F₆(x) = x²-x+1

Si n es primo, entonces el polinomio ciclotómico F_n es completo de grado (n-1). En general, el grado de F_n(x) es igual al número de enteros menores que n y coprimos (sin divisores comunes) con n.

De hecho, una definición alternativa de los polinomios ciclotómicos es esta:



donde k toma sólo valores desde 1 hasta n que sean primos con el propio n.

Siendo los correspondientes números de Moivre.

Lo curioso del asunto es que con tal definición, siempre resulten polinomios de coeficientes enteros.
Además, todos los coeficientes parecen ser igual a la unidad con signo más o menos, o cero.

Este extremo ilustra el papel relativamente poco significativo que representan las conjeturas en matemáticas, y que hemos resaltado muchas veces desde este blog. En efecto, es natural viendo que los primeros polinomios ciclotómicos tienen siempre sus coeficientes con estos valores, conjeturar que ocurre así para todo n.

Si seguimos calculándolos, podremos comprobar que entre los cien primeros, ninguno incumple esta norma.

En las ciencias experimentales, cuando las observaciones dan la razón a la teoría, ésta sale reforzada. Esta forma de acceso a la verdad en matemáticas no es satisfactoria: en matemáticas las hipótesis no valen nada mientras no se demuestren. Y cien casos demuestran el caso general tan poco como diez mil o mil millones...

Lo extraordinario del caso es que nuestros polinomios ciclotómicos no cumplen la conjetura anterior: el primero que la incumple es el de puesto 105, que vale:

F₁₀₅(x) = x⁴⁸ + x⁴⁷ + x⁴⁶ - x⁴³ - x⁴² - 2x⁴¹ - x⁴⁰ - x³⁹ +x³⁶ + x³⁵+x³⁴ + x³³ + x³² + x³¹ - x²⁸ - x²⁶ - x²⁴ - x²² - x²⁰ +x¹⁷ + x¹⁶+ x¹⁵ + x¹⁴ + x¹³ + x¹² - x⁹ - x⁸ - 2x⁷ - x⁶ - x⁵ + x² + x + 1

como pueden observar, dos de los coeficientes son sendos doses.

De hecho, se ha demostrado que existen coeficientes tan grandes como se quiera para polinomios de puesto suficientemente elevado.

En la figura que encabeza este post pueden ver las gráficas de los cinco primeros polinomios ciclotómicos.

Grupos cíclicos (y 2)

Decíamos en el post anterior que un grupo cíclico era el que se generaba a partir de uno sólo de sus elementos, y escribíamos G=[a] para indicar que dicho elemento a de G era generador de todo el grupo.
Con el grupo de giros del selector de siete posiciones del post anterior quedaba claro: el giro de un paso g₁ generaba todo G:

g₁²=g₂
g₁³=g₃
...
g₁⁷=g₀.

Si seguimos operando, volvemos a encontrar g₁,g₂,..., y ahora se ve claramente el significado profundo del apelativo cíclico para este tipo grupos.

En suma: los productos de operar g₁ consigo mismo son {g₁,g₂,g₃,g₄,g₅,g₆,g₀}, que es el grupo entero.

SI lo intentamos con otro elemento, g₂, por ejemplo, obtenemos:

{g₂,g₄,g₆,g₁,g₃,g₅,g₀}, que vuelve a ser el grupo completo.

Podríamos hacer lo mismo con todos los elementos: cualquier elemento de G genera todo G, por lo tanto podemos escribir:

G=[g₁]=[g₂]=[g₃]=[g₄]=[g₅]=[g₆]=[g₇].

Sin embargo esta situación no es la general: si el grupo original tuviera 8 elementos, el elemento g₂ generaría al subgrupo H={g₂,g₄,g₆,g₀}, que es la mitad de todo el grupo original.

En el fondo la explicación es muy sencilla, y se ha apuntado en los comentarios del post anterior: a base de giros de orden par sólo podemos generar otros giros de orden par si es asimismo par el número de elementos del grupo original, y nunca generaremos uno impar. Lo mismo vale para los múltiplos de cualquier otro número diferente del dos.

El conjunto de todos los elementos generados por uno, sea o no sea el grupo total es siempre a su vez un grupo (subgrupo propio o impropio del original. Llamamos propio si es estrictamente menor que el de partido, e impropio si es él mismo. Pues bien: el Teorema de Lagrange recoge este aspecto en toda su generalidad.

Un enunciado light del mismo es:

Dado un grupo G de orden n, si H es un subgrupo de G entonces el orden de H, o(H) es divisor de n

Dado que el conjunto de elementos generado por un elemento es siempre un subgrupo, resulta que su número de elementos será siempre divisor del orden del grupo total o(G)=n.

Y sólo en el caso en que n sea primo (como en el ejemplo anterior, con n = 7), tendremos asegurado que cualquiera de los n elementos generará el grupo completo, porque al no tener ndivisores, el orden de los subgrupos será igual a n, salvo en el caso del elemento neutro g₀, que tendrá orden 1, e incluirá al citado g₀ él sólo.

Los grupos cíclicos tienen más propiedades que los hacen importantes: la primera es que son necesariamente abelianos (conmutativos), y la segunda es que el Teorema de Lagrange es inversible para ellos.

Lo primero quiere decir que g_j*g_k=g_k*g_j, para toda pareja de elementos de G, y lo segundo merece una explicación más tranquila:

El Teorema de Lagrange afirmaba que los subgrupos de un grupo G de orden n, de existir, tenían un orden m que era divisor de n.

Su inversión indica que dado m, para cada divisor n, existe un subgrupo con dicho número de elementos.

El teorema original lo cumplen todos los grupos, su inversión sólo algunos, los cíclicos entre ellos.

Ahora estamos en condiciones de demostrar un terorema interesante y muy sencillo, que afirma que Si el orden de un grupo es primo, entonces dicho grupo es cíclico

Lo demostramos:

Sea o(G)=p, con p primo.

Sea a un elemento de G, diferente del elemento neutro. H=[a] es un subgrupo generado por a, y su orden, por el teorema de Lagrange será divisor de p. Dado que p es primo y no puede ser o(H)=1 pues a no es el neutro, entonces necesariamente o(H)=p, con lo que H=G, y G=[a].

Con esto terminamos nuestra incursión en los grupos cíclicos. La teoría de grupos es una rama del álgebra muy abstracta. Normalmente un libro sobre este tópico es un tocho de cientos de páginas sin ilustración alguna. No obstante, y dada la belleza del asunto es evidente una vez más que la belleza de la matemática no está en las ilustraciones...

Salvo los preliminares de la teoría, el resto en profundidad es para verdaderos especialistas. Felices ellos que están en disposición de saborear tales frutos.

____________________________________________________________________

HACE UN AÑO hablábamos de la matemática de la música. En una serie de tres post explicábamos los motivos por los que las notas musicales son siete (do,re,mi,fa,sol,la y si), doce si tenemos en cuenta sus correspondientes alteraciones; y no treinta o dieciocho.