Polinomios ciclotómicos

Hemos explicado en post recientes que las raíces de la unidad se distribuyen a lo largo de la circunferencia unidad en el plano complejo, dividiéndola en n partes iguales. Vimos que cada uno de los valores de la raíz n-ésima de la unidad se podía expresar mediante el número complejo e^i(2PI/n)k. Dando valores a k desde 1 hasta n obtenemos todas las raíces. No lo dijimos en su momento, pero a dichos números complejos unitarios se les denomina números de Moivre .

Estas raíces son las soluciones de la ecuación polinómica :

xⁿ=1

Pues bien, a aquellos polígonos irreducibles cuyas raíces son raíces de la unidad se llaman Polinomios ciclotómicos . Esta bella palabra significa etimológicamente “que corta a la circunferencia”; como podemos ver tienen el nombre muy bien puesto. No son ellos quienes cortan a la circunferencia en R ², sino sus raíces en el plano complejo.

Nuestro polinomio genérico xⁿ-1 no será ciclotómico para todo valor de n. De hecho lo será sólo para n=1. El motivo es que en la propia definición de Polinomio ciclotómico se expresa que dicho polinomio debe ser irreducible.

Los polinomios son expresiones en forma de suma de potencias de ciertas variables, denominadas indeterminadas . Consideraremos únicamente polinomios racionales de una indeterminada. Su forma genérica es:

P(x)=a_nxⁿ+a_n-1x^n-1+ a_n-2x^n-2+...+ a₁x+a₀

Los números a_n son los coeficientes; que pertenecerán al cuerpo de los racionales.
Pues bien; el conjunto de todos los polinomios con la operación suma y producto habituales resulta ser un anillo, que llamaremos Z[x] o Q[x], para el caso de que los coeficientes sean enteros o racionales.
Z[x] o Q[x] resultan ser anillos y no cuerpos, y la relación de divisibilidad entre los polinomios se define al uso:

Diremos que un polinomio P(x) divide a otro Q(x) cuando existe un tercero
Z(x) tal que Q(x)=Z(x)·P(x)

Diremos que un polinomio es irreducible cuando no puede expresarse como producto de otros dos. Por lo tanto, obtendremos los sucesivos polinomios ciclotómicos factorizando los polinomios genéricos xⁿ=1.

El primero de ellos provendrá de la ecuación x=1; y por lo tanto es
F₁(x)=x-1.

Para n=2, tenemos x²=1, que en forma de polinomio es x²-1 Ahora bien; este polinomio se puede expresar como (x+1)·(x-1). Como el segundo factor era el primer polinomio ciclotómico, el otro es nuestro segundo:
F₂(x)=x+1.

Si continuamos, para n=3 tenemos que el polinomio x³-1 es divisible por (x-1), pudiendo ser factorizado así: x³-1=(x-1)·(x²+x+1)

Este último factor es por tanto el tercer polinomio ciclotómico:

P₃(x)= x²+x+1

Esa es la pauta para la obtención de los sucesivos polinomios ciclotómicos

· F₁(x) = x-1
· F₂(x) = x+1
· F₃(x) = x²+x+1
· F₄(x) = x²+1
· F₅(x) = x⁴+x³+x²+x+1
· F₆(x) = x²-x+1

Si n es primo, entonces el polinomio ciclotómico F_n es completo de grado (n-1). En general, el grado de F_n(x) es igual al número de enteros menores que n y coprimos (sin divisores comunes) con n.

De hecho, una definición alternativa de los polinomios ciclotómicos es esta:



donde k toma sólo valores desde 1 hasta n que sean primos con el propio n.

Siendo los correspondientes números de Moivre.

Lo curioso del asunto es que con tal definición, siempre resulten polinomios de coeficientes enteros.
Además, todos los coeficientes parecen ser igual a la unidad con signo más o menos, o cero.

Este extremo ilustra el papel relativamente poco significativo que representan las conjeturas en matemáticas, y que hemos resaltado muchas veces desde este blog. En efecto, es natural viendo que los primeros polinomios ciclotómicos tienen siempre sus coeficientes con estos valores, conjeturar que ocurre así para todo n.

Si seguimos calculándolos, podremos comprobar que entre los cien primeros, ninguno incumple esta norma.

En las ciencias experimentales, cuando las observaciones dan la razón a la teoría, ésta sale reforzada. Esta forma de acceso a la verdad en matemáticas no es satisfactoria: en matemáticas las hipótesis no valen nada mientras no se demuestren. Y cien casos demuestran el caso general tan poco como diez mil o mil millones...

Lo extraordinario del caso es que nuestros polinomios ciclotómicos no cumplen la conjetura anterior: el primero que la incumple es el de puesto 105, que vale:

F₁₀₅(x) = x⁴⁸ + x⁴⁷ + x⁴⁶ - x⁴³ - x⁴² - 2x⁴¹ - x⁴⁰ - x³⁹ +x³⁶ + x³⁵+x³⁴ + x³³ + x³² + x³¹ - x²⁸ - x²⁶ - x²⁴ - x²² - x²⁰ +x¹⁷ + x¹⁶+ x¹⁵ + x¹⁴ + x¹³ + x¹² - x⁹ - x⁸ - 2x⁷ - x⁶ - x⁵ + x² + x + 1

como pueden observar, dos de los coeficientes son sendos doses.

De hecho, se ha demostrado que existen coeficientes tan grandes como se quiera para polinomios de puesto suficientemente elevado.

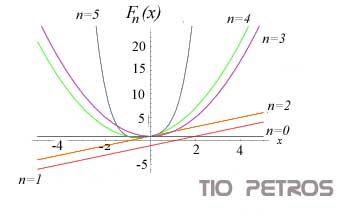
En la figura que encabeza este post pueden ver las gráficas de los cinco primeros polinomios ciclotómicos.

9 comentarios

[Fernando Muñoz - 19 de octubre de 2010 - 01:48]

hola necesito un articulo a cerca de los polinomios ciclotomicos si alguin me colabora, gracias mi correo [e-mail]

[yo - 26 de agosto de 2008 - 21:44]

para demostrar que los polinomios ciclotomicos son irreducibles se le aplica el criterio de Eisenstein al polinomio F(x+1) donde F es el ciclotomico.

[kathy - 12 de noviembre de 2007 - 19:03]

alguien me puede decir si existe otro polinomio ciclotómico en que suceda lo del 105º ...o este es unico??

[carlos - 23 de agosto de 2007 - 02:10]

Para ti Juan
usa el triangulo de tartaglia
del 1 5 10 10 5 1, que son los coeficientes de tu binomio a la 5

[Esteban - 03 de julio de 2006 - 22:07]

- Como demuestro que el polinomio coclotomico es irreducible?
Gracias!

[jogeisy - 09 de mayo de 2006 - 17:10]

necesito con urgencia un texto donde me digas el nombre de la persona quein invento los polinomios por fa please

[Juan - 10 de noviembre de 2005 - 23:40]

puede explicarme alguien cuales son los pasos para hacer por ejemplo (3a+2b) elevado a la 5 sin tener que multiplicarlo 5 veces????

[Anónimo - 24 de septiembre de 2005 - 17:41]

[icp - 24 de enero de 2005 - 13:12]

Muy interesante lo del 105º polinomio ciclotómico, la verdad es que nunca se me pasó por la cabeza(cosas de estar más acostumbrado en este tema a Z2 o Z3 donde sus coeficientes deben ser siempre -1, 0 ó 1) preguntarme cual era el primer polinomio ciclotómico con esa propiedad, en realidad es curioso que haya que "avanzar" tanto para encontrar uno. Por cierto, ya que los polinomios ciclotómicos que ocupan posiciones primas sí que cumplen eso(en este caso el coeficiente es 1 siempre),ahora me pregunto qué pasa con los que son potencia de primos.