Atrapando el concepto de azar (5)
A lo largo de estos tres posts repasamos hace unos meses el concepto de continuidad en espacios generales. Decíamos allí que la continuidad de una función entre dos espacios topológicos era una propiedad relativa, no absoluta de la función. Unas topologías harían continua una determinada función y otras no. La noción de proximidad surgía de la topología sin necesidad de tener una métrica o forma de medir distancias definida, y decíamos que:
Una función continua en un punto p transforma puntos próximos a p en puntos próximos a f(p), y esa proximidad se establece en virtud de los entornos de las respectivas topologías.
Otra forma de decirlo es que la función, para ser continua debe "ser respetuosa" con las topologías de partida y de llegada.
El concepto de función continua y de función medible es radicalmente diferente, pero operativamente análogo.
En el caso que nos ocupa, no tenemos espacios topológicos, sino espacios de medida , que como hemos dicho son una tríada (X,A,M), donde X es un conjunto cualquiera, A es una sigma-álgebra subre X y M es una medida definida en A.
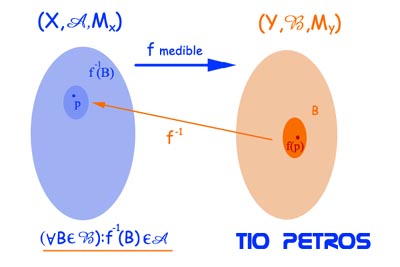
Supongamos que tenemos dos espacios de medida: (X,A,MX) y (Y,B,MY); y una aplicación f de X a Y. Diremos que f es una función medible cuando la antiimagen de todo subconjunto de Y que sea elemento de B es un subconjunto de X que es a su vez elemento de A.
De esta forma, la función es respetuosa con las sigma-álgebras de partida y de llegada.
Este aparente galimatías esconde una idea extremadamente sencilla: los elementos de las respectivas sigma-álgebras son simplemente aquellos subconjuntos para los cuales tiene sentido aplicar el concepto de medida, y por ello se denominan conjuntos medibles . La propiedad pedida a las funciones medibles exige que cada medible del conjunto de llegada tenga un alter ego medible en el conjunto de partida del cual es imagen por dicha aplicación.
Es fácil comprender que este tipo de funciones son las interesantes entre espacios medibles.
Las variables aleatorias que aún estamos por definir son aplicaciones medibles entre dos espacios de medida: el origen es un espacio probabilístico (X,A,P), donde P es una medida definida en X tal que P(X)=1, y por lo tanto es una probabilidad. Y el de llegada es en conjunto de números reales R.
Lo único que nos falta es dotar a R de una sigma-álgebra para tener el panorama completo. Y eso es muy fácil de hacer: la medida en R será la extrapolación de la noción intuitiva de longitud a todos los conjuntos medibles de R. Esta medida se denomina medida de Lebesgue . Definir la medida de Lebesgue es dar una pauta para encontrar la medida de cualquier subconjunto medible de R. Como cualquiera de tales elementos debe poder ser obtenido por uniones y pasos a complementario de elementos, en virtud de la definición de sigma-álgebra, definiremos tales elementos primitivos como los intervalos [a,b], y definiremos su longitud como el número real l[a,b]=b-a.
Las propiedad sigma-aditividad de la medida junto con las propiedades generales de toda sigma-álgebra nos facilita definir la medida de cualquier subconjunto que pertenezca a esta sigma-álgebra generada por los intervalos de la recta real. Recibe el nombre de sigma-álgebra de Borel , y sus elementos se denominan borelianos .
Es mucho más fácil encontrar borelianos en la recta que no borelianos. Cualquier cosa incluida en Rque se imaginen (a no ser que sepan mucho o tengan mucha imaginación) es un boreliano. Los intervalos lo son, sean abiertos o cerrados (radical diferencia con las topologías),los puntos aislados lo son también... efectivamente, por uniones, intersecciones finitas o infinitas numerables, y con pasos a complementario (operaciones permitidas en las sigma-álgebras) lo podemos conseguir casi todo.
Es ese casi el que complica tanto la teoría de la medida: existen como anunciábamos ciertos subconjuntos de R tan endiablados que no son borelianos, y para ellos no se puede definir medida alguna. Estos elementos son los que posibilitan en R3 cosas tan inexplicables como la paradoja de Tarski-Banach , de la que hablamos en su día aquí.
Tenemos la estructura montada. En el próximo post veremos la definición rigurosa de variable aleatoria y comprenderemos mejor esa idea intuitiva de que una variable aleatoria es una variable que toma valores en función del azar. Entonces comprobaremos que no es una ocurrencia pedir que sea una función medible, sino que esta propiedad es la que nos posibilitará a inducir una probabilidad en R.
Seguiremos dentro de unos días.
5 comentarios
Sildenafil -
Jesus Daniel -
Que conjunto en los reales es un no boreliano?? Un ejemplo.
Anónimo -
robrto torres -
roberto torres -