Atrapando el concepto del azar ( y 6)
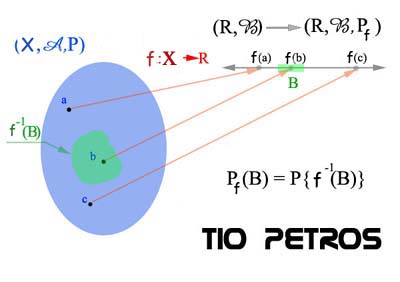Ya estamos en condiciones de definir una variable aleatoria como una función medible de un espacio probabilístico (X,A,P) en el espacio medible (R,B), donde ,B es la sigma-álgebra de Borel definida en R. Todos los conceptos están definidos en los cinco posts anteriores.Sea f tal variable aleatoria. Para ver la importancia de que f sea medible, repetiremos la definición de función medible dada en el post anterior:
Diremos que f es una función medible cuando la antiimagen de todo subconjunto de R que sea elemento de B es un subconjunto de X que es a su vez elemento de A.
Esto significa que todo subconjunto medible de la recta real tiene un subconjunto medible del espacio probabilístico del cual es imagen. Tenemos una probabilidad definida en el espacio de partida, pero no en el de llegada. En virtud de la medibilidad de f, podemos considerar ahora una probabilidad inducida en R.
En efecto, si B es un boreliano de R, tenemos la probabilidad inducida indicada por la siguiente ígualdad, que dada su importancia conceptual me permito escribir en caracteres grandes:
Pf{B} = P{f-1(B)}
La probabilidad original es P, y está definida en el espacio probabilístico original (X,A,P); la probabilidad inducida es Pf, definida ahora en lo que hasta ahora era simplemente un espacio de medida de con la medida de Lebesgue , y ahora es ya otro espacio probabilístico.
La variable aleatoria toma medidas en R, y para nosotros éste segundo espacio probabilístico inducido, (R,B,Pf) será lo más visible del problema en cuestión. Nuestros cálculos sobre probabilidades los haremos en muchas ocasiones sin preocuparnos del espacio de partida; y a menudo quedará totalmente a la sombra, si bien es el que maneja las cuerdas del azar.
Esto se verá mejor con algún ejemplo:
Partíamos en esta serie de posts sobre el azar de dos experimentos aleatorios:
Experimento A: tirar un dado no trucado una vez.
Experimento B: elegir un número con equiprobabilidad en el intervalo [0,1]
Ambos experimentos definen los espacios probabilísticos de partida. De momento no hay variable aleatoria alguna definida.Definamos ahora dos variables aleatorias sobre ellos:
Para el primer experimento, f1 definida como un pago en miles de euros igual a la puntuación sacada en el dado. Para el segundo experimento, f2 un valor de 100 si el numero es mayor que 0,5 y un valor de 100 si el número es menor o igual que 0,5.
Ahora, podemos abstraernos de las naturalezas de los espacios probabilísticos de partida, porque podemos hablar de probabilidades en los espacios de llegada; probabilidades inducidas por las variables aleatorias y por las probabilidades.
En efecto, en el primer caso, obtenemos 1000, 2000, 3000, 4000, 5000 ó 6000 euros con la misma probabilidad de 1/6. Esto nos basta para cortar las amarras que nos unían al espacio (X,A,P) original, en el que X={1,2,3,4,5,6}, y contemplar únicamente la distribución de premios con sus respectivas probabilidades que es lo que nos interesa. Ahora podemos responder a cuanquier pregunta del tipo:
¿Qué probabilidad tenemos de ganar más de X euros?
¿Qué probabilidad tenemos de ganar entre X e Y euros?
En la pregunta podemos incluir cualquier subconjunto de R que sea medible Borel. Parece que en este ejemplo tan sencillo estamos matando mosquitos a cañonazos. Efectivamente, el arsenal matemático empleado es desproporcionado; pero eso es tan sólo porque el ejemplo era trivial. En ejemplos más elaborados la cosa cambia.
En nuestro segundo ejemplo la variable aleatoria tan sólo puede tomar dos valores: +100 ó 100. Por tanto, el conjunto {+100,-100} de R es todo el recorrido de la variable aleatoria f2 . Sin embargo, sigue siendo cierto que f2 define una probabilidad condicionada en toda la sigma-álgebra de Borel de R.
Cada elemento de dicha sigma-álgebra de partida es un posible resultado del experimento de elegir con equiprobabilidad un punto en el intervalo [0,1]; así, B={0.25} es salir elegido el 0,25; y B=[0,1/2) es salir elegido un número menor que 1/ 2, mientras que B= [0,1/2) U (1/2,1] es no salir elegido el 1/ 2 . Todos ellos tienen una probabilidad asociada por el simple hecho de ser (X,A,P) un espacio probabilístico. Ahora, cada BR (el subíndice es para recalcar que ahora estamos refieriéndonos a la sigma-álgebra del conjunto de llegada) de la sigma-álgebra de Borel de R tiene también una probabilidad inducida asociada, que es la probabilidad de que la variable aleatoria tome un valor que esté incluido en B.
Así, BR=[1,inf) es el suceso la variable f2 toma un valor mayor o igual que la unidad.
En este ejemplo tan sencillo, la probabilidad Pf2 inducida es la siguiente:
Pf2(B)= 0 , si {-100,+100} no está en B
Pf2(B)= 1, si {-100, +100} está en B
Pf2(B)= 1/ 2, si tan sólo uno de los dos valores 100, +100 está en B.
Y desde este momento, podemos olvidarnos del espacio probabilístico de partida y trabajar tan sólo con la variable aleatoria. De hecho, la propia existencia de los espacios probabilísticos y sus sigma-álgebras, tanto de salida como de llegada pueden quedar oscurecidos al trabajar con un problema concreto. Pero siempre subyacen en el problema, dado cohesión teórica a todo el entramado.
Un profesor, decía que los espacios probabilísticos son como Rebeca, la de la película de Hitchcock. Todo gira alrededor de Rebeca, aunque no se le ve por parte alguna.
Pero sin Rebeca no habría película...
3 comentarios
Javier Maldonado -
Gracias
José María -
Andrés -