Blogia
Tio Petros

Cuádrame esta lúnula.

- Conceptos
Cuádrame esta lúnula. En una ocasión, hablamos de los ingenuos trisectores de ángulos.

Llamábamos así a estas personas empeñadas en demostrar lo imposible. Existe una fauna muy variada de personajes de este pelo; en cuestiones físicas se agolpan alrededor del mito de la máquina de movimiento continuo, y en matemáticas alrededor de tres problemas imposibles: la duplicación del cubo, la trisección de un ángulo cualquiera y la cuadratura del círculo .

Decíamos entonces que la imposibilidad de estas tres construcciones se debe a resultados que provienen de la teoría de Galois, y que se resumen en dos proposiciones, ambas perfectamente consolidadas, demostradas y admitidas por la comunidad matemática desde hace muchísimo tiempo:

1.- Todos los números de Q son construibles.

2.- Un número real es construible si y solo si es solución de una ecuación de grado potencia de dos en Q
La cuadratura del círculo implica al número pi, que no es solución de ningún polinomio en Q, la duplicación del cubo implica la construcción de la raíz cúbica de dos, que es solución de un polinomio de grado tres (no es potencia de dos), y la trisección del ángulo de 60º implica la construcción de otro número solución de una ecuación de grado tres, y por lo tanto las tres son imposibles. Pueden existir métodos para trisecar un ángulo concreto (el del ángulo recto es trivial), pero nunca, NUNCA el de 60º.

Sucede que existen ciertos problemas parecidos en apariencia a los tres anteriores, que sí son posibles, y vamos a ocuparnos de uno de ellos: la cuadratura de la lúnula de Hipócrates .

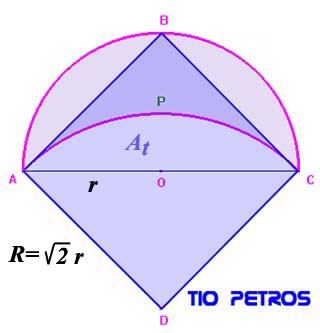
Una lúnula es la porción de plano comprendida entre dos arcos de circunferencia. En la figura tienen una lúnula de Hipócrates , que es una lúnuna con las proporciones dadas por las dimensiones de un cuadrado ABDC. Uno de los dos arcos es el ABC, con centro en 0 y radio r = OA. El otro es el APC, con centro en D y radio R = AD.

El área de la lúnula es la diferencia entre el semicírculo de centro en O y radio OA y el sector circular APC

Llamemos AL al área de la lúnula; As al área del semicírculo y At al área del sector antes citados.

Tenemos AL = As - At
Y desarrollando podemos escribir:



Así pues, el área de la lúnula es r 2, y como r 2=R2/2, tenemos que el área de la lúnula es la mitad del área del cuadrado ABCD, o lo que es lo mismo: es igual al área del triángulo ABC, todo ello perfectamente construible con regla y compás a partir de la lúnula.

¿A que es sorprendente un área de una figura limitada por arcos de circunferencias en la que no aparece pi?

Y es que la resta de dos números irracionales ( o en este caso lo que es aún peor: transcendentes) bien puede ser un número racional.

En el fondo no hay misterio alguno: la explicación radica en la igualdad de dos áreas: el área As del semicírculo ABC, y el área del cuadrante de círculo de centro en D y radio R. Llamemos X a dicho área.

El área de la lúnula es igual a la diferencia entre As y At. La primera vale X y la segunda vale (X -Q) siendo Q el área del triángulo ADC.

Por ello, el área buscada vale

AL = X - (X -Q) = Q.

Tanto (X -Q) como X son trascendentes, no así Q, que es un número bien racional.

9 comentarios

Goyo -

1. El compás no tiene que estar oxidado, puede relucir hasta deslumbrar.

2. No vale decir que el problema tiene solución si eliminas las restricciones porque las restricciones son parte del problema. Si eliminas una restricción ya no es el mismo problema, es otro distinto.

Juan Fer -

Muy interesante este articulo de la lunula de Hipocrates, pero temo decirte que los tres problemas clasicos griegos si tienen solucion, pero de una manera "mecanica", la restriccion principal es que estos problemas solo se deben de hacer con una regla sin graduar y con un compas oxidado, y asi ya no tienen solucion, pero no son puramente irresolubles. Por ejemplo con esta lunula de hipocrates, nos acercariamos a la cuadratura del circulo, en donde si duplicamos el area de la lunula del dibujo y la colocamos abajo, tendriamos un circulo con un hoyo semielipsoidal en medio,parecido a un ojo, en donde los parpados serian las dos lunulas que en conjunto me crean el area del cuadrado y la pregunta sería entonces... ¿cuanto mide el hoyo dentro del circulo?

Angela -

Estoy estudiando Bellas Artes y justo en Geometria Descriptiva estamos dando ete tema. Lo que pasa es que creo que en esta dirección lo explica mucho mejor. Hipócrates cuadró ESTE tipo de lúnula, hecha perviamente a partir de un semicírculo, también resolvió dos tipos de lúnulas más. Pero si tú intentas cuadrar una lúnula qualquiera no te saldrá. Más información en este pdf interesante sobre ello: http://www.emis.de/journals/BAMV/conten/vol11/Pi_def.pdf

daniela -

meparecio fantastica es ta pajina

Crystal -

¡Caray! Qué chulada, a mí las lúnulas me sonaban... pero como el que oye campanas, jeje. Gracias por el post!

Goyo -

Antón, se trata de otro Hipócrates. Fueron contemporáneos (más o menos, s. V y IV a.c.) El médico era de Cos y éste de Quios, fíjate qué cosas.

Lo que me choca es que se llame a ésta precisamente "lúnula de Hipócrates". El tipo estudió muchas lúnulas y consiguió cuadrar un buen puñado de ellas, si no recuerdo mal.

Tio Petros -

Hola Acapulco. Pues no sé. Los usuarios de blogia tenemos las herramientas que tenemos, y esa no la conozco. Siempre puedes mandar a tu amigo la dirección de este artículo...
Gracias por tu interés.

Acapulco -

Como Anton, yo tampoco conocia la lunula, y es preciosa...

Por lo mismo, he querido mandar este articulo a una persona. Cuando al buscar la opcion, no la encontre, se me vino a la mente que quizas seria buena idea integrar esta funcion. Que te parece Tio Petros?. Factible?

Antón -

Me ha encantado el post. No conocía la lúnula, y realmente ha sido una sorpresa ver que en su área no figura pi en lado alguno.
A todo esto: ¿el Hipócrates que da el nombre a esta figura es el médico, el del juramento hipocrático?