Dios es un ludópata (1)
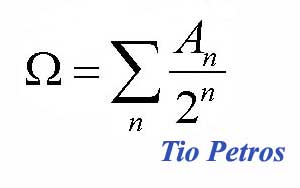A Einstein no le habría gustado este post. Uno de los padres de la mecánica cuántica renegaba de la criatura con la frase Dios no juega a los dados.Churchil era un buen creador de frases de complejidad irreductible: pensamiento condensado en pocas palabras, y nuestro bienamado Albert no le iba a la zaga. A Einstein no le gustaba el azar, y creía en la existencia de variables ocultas, que es otra forma de decir que lo que parece azar no es sino falta de información por nuestra parte.
En el fondo, me parece a mi que la cuestión es muy poco científica: nos gusta o no nos gusta que el azar y el caos esté formando parte de la substancia misma de las cosas en función de nuestras apetencias, criterios, opiniones e ideología. Pero una de las pocas propiedades del universo de la que podamos estar seguros es la nula atención que presta a nuestros gustos particulares.
En una visión superficial del asunto, alguien podría decir que la matemática acepta desde siempre el azar; al fin y al cabo tenemos la teoría de probabilidades aceptada y bien establecida desde hace mucho tiempo. Pero la cosa no es tan sencilla.
La teoría de la probabilidad actual parte de la axiomatización de Kolmogorov, auxiliada por la teoría de la medida, y es un edificio muy bien construido; eso es cierto. Sin embargo, nada dice de el origen del azar, ni de la posibilidad de que tal azar sea desconocimiento por nuestra parte, existencia de variables ocultas, o que por el contrario sea parte integrante de la estructura de las cosas.
Aunque no lo parezca, el origen de esta historia está en el Entseidungsproblem de Hilbert. Cuando Hilbert puso los deberes para el nuevo siglo XX, una de la cuestiones planteadas era la siguiente:
¿Todo problema matemático tiene una solución algorítmica? O en otras palabras, a todo problema especificable formalmente, ¿se le podrá dar una solución mecánica en una cantidad finita de pasos?
En 1931, el matemático austríaco-alemán Kurt Gödel dio un paso fundamental para dar una respuesta cuando demuestra el celebrado Teorema de Incompletitud , ya hemos hablado de ello en este blog. Y fue Alan Turing en 1936 quien consigue dar la respuesta definitiva a la pregunta de Hilbert: No todo problema matemático tiene solución algorítmica. Para demostrarlo inventó la noción matemática de computadora de propósito general. Básicamente, Turing define la computadora y plantea un problema sobre ella para el cual demuestra que no hay ningún algoritmo que lo resuelva. Es el problema de la detención (en Inglés se llama Halting problem); informalmente ya lo conocen: es el problema de saber si un programa se cuelga cuando corre en la computadora. El problema de la detención es indecidible, como demostró Turing.
Así pues, debemos hacer un alto para recordar una verdad que muchas veces se olvida. Haré algo de cosmética para resaltar la siguiente frase lo suficiente:
*********************************************************************
*********************************************************************
Las computadoras no se idearon para meter videojuegos, ni para chatear con los amigos: se inventaron para responder a una importante pregunta filosófica
*********************************************************************
*********************************************************************
Un matemático norteamericano de ascendencia argentina, Gregory Chaitin, pensó en este asunto en términos de azar. ¿Dónde entra el azar en todo esto? Pues muy fácil.
De la imposibilidad dada por el teorema de Turing de resolver el problema de la detención, pasamos a preguntarnos por la probabilidad de parada de un algoritmo. Cada algoritmo es en definitiva una lista finita de ceros y unos. Con unos programas (los bien constituidos), la máquina se detendrá convenientemente, y con otros se quedará colgada. Supongamos que escribimos un programa a base de n ceros y unos tirando una moneda al aire n veces, existen 2 n programas posibles. Por lo tanto la probabilidad de obtener un programa concreto de n bits es 2 -n. De todos estos programas, una parte muy pequeña acabarán en la instrucción FIN DE PROGRAMA correctamente. Sea A n el número de programas correctos desde este punto de vista, de n bits. La probabilidad de generar aleatoriamente un programa de n bits que detenga la máquina será:
Pn= A n· 2 -n.
Y si extendemos a todos los programas posibles finitos obtenemos la constante Omega de Chaitin que cabeza este artículo.
En matemáticas, a diferencia de la física, las constantes fundamentales son pocas. Tenemos el número e, tenemos pi, la constante de Euler, la de Feigenbaum y ahora tenemos la constante de Chaitin.
Existe toda una jerarquía de números en cuanto a la maldad que exhiben (permítanme el antropomorfismo, estamos en el post cuarentaytantos, y ya habrán aprendido a leerme entre líneas... )
Algunos números exhiben poca maldad, como los enteros. Los irracionales son bastante traviesos, y entre ellos los trascendentes son los peores. Pues bien: la omega de Chaitin es el demonio en persona.
La constante de Chaitin nos introducirá en el caos, y nos hará volver a considerar el papel del azar en el centro mismo de la matemática, terminaremos afirmando que si Dios no juega a los dados es porque está muy ocupado con la ruleta y las cartas, pero eso será en el siguiente post.
Como siempre, si ustedes quieren.
11 comentarios
cian -
de acuerdo con esto, todas las formulas de la energia me expresan la existencia de la materia, y que en especial la de e=mc2 su proporicionalidad (de la materia y la energia). luego, veo en algunos escritos que la materia es energia condensada, cuando yo tenía por definiciones de E: como o bien capacidad para mover una masa a una distancia, o bien como medida del movimiento de la materia. y me dicen que la materia es una forma de energia: energia congelada o concentrada. para mí eso es un absurdo.
no se tu que opines al respecto. si me puedes aclarar mi confusion
Angel Alvarez -
mig21 -
Si, es algo parecido a lo que yo quería decir... Es cierto que hay constantes(?) universales, pero que en el marco de un determinado desarrollo o de una teoría no es relevante el valor que toman, es más importante las relaciones entre las magnitudes que las magnitudes en si.
En lo que ciertamente tienes razón es en que preguntándonos porqué tienen esos valores podemos encontrar más información acerca de como se organiza la materia y el espacio. Un ejemplo es la teoría de quarks, en la que preguntándose por las relaciones de las masas (y otras propiedades) de las partículas se puede deducir que son combinaciones de otras más elementales (lo que por cierto tiene mucha relación con la matemática, teoría de grupos y representaciones... algo que lamentablemente falla en mi formación académica)
En fín para mi (punto de vista completamente subjetivo) la física y la matemática se alimentan tanto mutuamente y tienen los límites tan borrosos que las considero parte de lo mismo. Es cierto que la matemática tiene la belleza de lo puro y de lo abstracto...
Ah, y gracias Tío Petros por dejarnos divagar aquí :)
Saludos
Crystal -
Creo que me quedaré con "la constante del demonio". Por cierto, que quizá otro día, Tío Petros, nos decidas ilustrar un poco más sobre esta constante y su relación con ese cosmos-caótico en el que los matemáticos viven entusiasmados.
Eratóstenes -
Para mi, "c" sólo es UNA de las constantes más importantes de la física. Básicamente, la teoría de la relatividad especial (incluido el famoso E=mc2) se deduce a partir de ella. Y todo "simplemente" porque "c" es una constante: la luz de mi lámpara o la que sale de la galaxia más veloz va siempre a la misma velocidad, exactamente "c" (unos 300.000 Km/s).
Pero la constante "c" no nos basta para describir nuestro mundo y eso es lo que (torpemente) quise decir en el comentario anterior. La masa del electrón, por ejemplo, es una cantidad constante en el universo, hasta donde sabemos. Y es tan constante e independiente como la velocidad de la luz. Podemos, a través de la ecuación E=mc2, calcular cuánta energía "contiene" el electrón, pero el resultado seguirá siendo otra constante (aunque en unidades de energía, y aquí está lo revolucionario).
Uno de los mayores misterios de la física es saber por qué la masa de cada partícula tiene ese valor precisamente. Quizá algún día alguien descubra que están relacionadas con la velocidad de la luz y la constante de Planck. Pero incluso en ese caso, necesitaremos una constante para cada partícula o al menos un término general
con unas constantes.
Lo que más temo ;-) es que las matemáticas y la geometría tendrán mucho que decir en el asunto. Ya en la actualidad, los físicos de partículas hablan de teoría de grupos, simetrías SU(n), supersimetrías...
Hay una diferencia fundamental con las matemáticas: las constantes físicas se determinan experimentalmente,
están sujetas a errores de medida, al principio de incertidumbre y puede que en algunos casos no lo sean; las constantes matemáticas lo son todo por si mismas.
Un saludo. Y gracias, Petros, por permitirnos hablar de estas cosas por aquí.
Tio Petros -
mig21 -
Me puedes explicar porque E=mc2 hace de c una constante realmente relevante. Es que no lo entiendo. Por lo que yo sé lo único que pone de relieve es que la energía y la masa son directamente proporcionales.
(No se si una discusión sobre lo similar o diferente de la matemática y la física es demasiado offtopic en este weblog)
Saludos y gracias
Eratóstenes -
En cuanto a las constantes físicas, hay muchas y fundamentales: La constante de gravitación o la masa del electrón no pueden expresarse en términos de la velocidad de la luz. Que la masa se exprese en Kg y que E=mc2 nos permite calcular la energía que tiene la masa de una partícula, pero no conocemos manera de calcular su masa a partir de la velocidad de la luz.
(Por cierto que se ha llegado a cuestionar si algunas permanecen constantes en el tiempo. Y estoy hablando de la velocidad de la luz).
Pero eso es otra historia y esto es un blog de matemáticas.
¿Qué hay detrás de la matemática? Mm, la Matemática es la única ciencia cuya belleza surge de si misma. ¿O será culpa del Tio Petros?
Pedro -
Por lo demás, genial la bitácoras. Gracias.
Tio Petros -
Respecto a los límites entre la física y las matemáticas, pues yo creo que son cosas diferentes. Detrás de la física está la realidad, el mundo que es su objeto de estudio, y detrás de la matemática está...esto es, está.... ejem...
Joder, qué postazo se puede hacer con esto!!!
Gracias por tu visita, y más aún por el comentario.
mig21 -
Me voy a permitir el lujo de intervenir aquí y en cierta manera llevarte la contraria....
Dices que "a diferencia de la física, las constantes fundamentales son pocas"... Bueno, no estoy de acuerdo con esa afirmación (si me lo permites :) )
Y me explico. Que yo recuerde, constantes universales físicas y relevantes (con esas tres características) sólo hay dos: la velocidad de la luz y la constante h (de Planck). El resto no son relevantes y con un cambio de unidades (coordenadas) desaparecen. En el fondo para los físicos teóricos ni siquiera éstas son relevantes: la energía es masa y la longitud de onda también energía. En el fondo no estoy seguro de los límites entre física y matemáticas (me gustan las dos)
Por lo demás muchas gracias por tu bitácora (y gracias a fernand0 por apuntar a ella)
Saludos