La conjetura de Borsuk ( y 2)
Seguimos con la conjetura de Borsuk, comenzada en el post anterior.
Cuando hablábamos de topología dijimos que a veces lo que está claro para dimensiones altas no lo está tanto para dimensiones bajas, cercanas incluso a nuestro mundo tridimensional.. De ahí que surja, por ejemplo, lo que se denomina topología de baja dimensión . En el caso que nos ocupa, sin embargo, pasa lo contrario.
La conjetura de Borsuk resulta ser cierta para dos y tres dimensiones. Sin embargo para dimensiones altas la cosa es muy complicada. Veamos por encima el asunto.
Para el caso tridimensional, la demostración tiene un atajo, basado en el siguiente teorema:
Todo objeto de tres dimensiones con diámetro d está contenido en un octaedro recto cuyas caras opuestas están a una distancia d unas de otras, y con tres de sus vértices truncados por planos perpendiculares s las diagonales, que distan d/2 del centro.
Puede parecer un poco complicado, pero con las siguientes figuras se ve mejor:
Aquí vemos tal octaedro con el truncado del primer vértice:
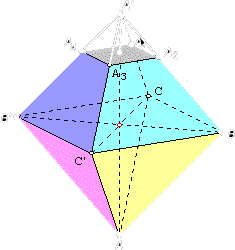
Ahora con tres de sus vértices de la misma manera:
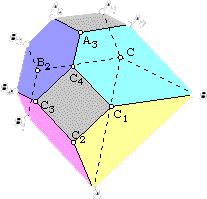
el teorema anterior dice que todo cuerpo tridimensional de diámetro d puede meterse dentro de este octaedro truncado, y resulta que sabemos dividir dicho cuerpo en cuatro partes para que todas tengan menor diámetro que el original, véanlo en la ilustración siguiente:
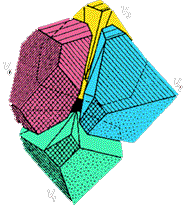
Ahora queda claro que el número de Borsuk para cualquier cuerpo de tres dimensiones es menor o igual a cuatro.
Es evidente que para dimensiones mayores no podemos seguir por ese camino. Por eso es comprensible que el reto quedara en suspenso durante muchos años.
Este estado de cosas cambió con la publicación por parte de los matemáticos J. Kahn y G Kalai en el Bulletin of the American Mathematical Society de un artículo que se titulaba Un contraejemplo de la conjetura de Borsuk .(1)
Lo que Kahn y Kalai hicieron fue demostrar que el número de Borsuk para cualquier objeto n-dimensional crecía exponencialmente con la dimensión. Más concretamente demostraron que cuando la dimensión crece hacia infinito, el número de Borsuk tiende asintóticamente a una función exponencial, que resultó ser la función siguiente:
g(n)=(1,1) SQR(n)
donde SQR(n) quiere decir raíz cuadrada de n.
Una de las propiedades de las funciones exponenciales es que por muy despacio que avancen al principio ( y esta lo hace muy lentamente, pues la base es cercana a la unidad, y el exponente no es n , sino su raíz cuadrada), siempre terminan por superar a cuanquier función polinómica. Concretamente la función f(n)= (n+1) que proponía la conjetura de Borsuk es polinómica de grado uno.
Para un valor de n = 9.162 la función exponencial g(n)=(1,1) SQR(n) comienza a ser mayor que (n+1), luego a partir de ahí la conjetura de Borsuk debe fallar necesariamente.
Este resultado zanja la cuestión de la validez universal de la conjetura, pero deja abierta una incógnita bastante incómoda.
Efectivamente, tal valor de la dimensión (n=9.162) es una simple cota máxima de cumplimiento de la conjetura: asegura que de ahí hacia arriba se deja de cumplir, pero nada dice de valores menores que 9.162. Bien pudiera ser que falle desde valore bastante menores.
Las sucesivas cotas de d han ido bajando : Nilli obtuvo el valor de 946, Raigorodsky 561 y Weissbach el de 560. Más recientemente, ya en el año 2.000, Aicke Hinrichs alcanzó el valor de 323. El artículo está disponible aquí.
EN todo caso,el tema está abierto. ¿Cuál es el valor de la dimensión para el cual la conjetura de Borsuk empieza a ser falsa?
______________________________________________________
HACE UN AÑO comenzábamos una serie de tres post para responder la pregunta ¿Qué es un número?
Vimos que contra la opinión general el número no es un concepto primigenio en la matemática, sino que se basa en el concepto anterior de conjunto.
En este post comenzamos a ver los axiomas en los que nos íbamos a basar, aquí desarrollamos la idea y finalmente concluimos con la extraordinaria idea de que fundamentación de los números naturales y la matemática toda está basada en el conjunto vacío. A Siddharta Gautama el Buda le hubiera gustado esta idea.
______________________________________________________
(1) J. Kahn & G. Kalai: A counterexample to Borsuk's conjecture, Bulletin Amer. Math. Soc. 29 (1993), 60-62.
Cuando hablábamos de topología dijimos que a veces lo que está claro para dimensiones altas no lo está tanto para dimensiones bajas, cercanas incluso a nuestro mundo tridimensional.. De ahí que surja, por ejemplo, lo que se denomina topología de baja dimensión . En el caso que nos ocupa, sin embargo, pasa lo contrario.
La conjetura de Borsuk resulta ser cierta para dos y tres dimensiones. Sin embargo para dimensiones altas la cosa es muy complicada. Veamos por encima el asunto.
Para el caso tridimensional, la demostración tiene un atajo, basado en el siguiente teorema:
Todo objeto de tres dimensiones con diámetro d está contenido en un octaedro recto cuyas caras opuestas están a una distancia d unas de otras, y con tres de sus vértices truncados por planos perpendiculares s las diagonales, que distan d/2 del centro.
Puede parecer un poco complicado, pero con las siguientes figuras se ve mejor:
Aquí vemos tal octaedro con el truncado del primer vértice:

Ahora con tres de sus vértices de la misma manera:

el teorema anterior dice que todo cuerpo tridimensional de diámetro d puede meterse dentro de este octaedro truncado, y resulta que sabemos dividir dicho cuerpo en cuatro partes para que todas tengan menor diámetro que el original, véanlo en la ilustración siguiente:

Ahora queda claro que el número de Borsuk para cualquier cuerpo de tres dimensiones es menor o igual a cuatro.
Es evidente que para dimensiones mayores no podemos seguir por ese camino. Por eso es comprensible que el reto quedara en suspenso durante muchos años.
Este estado de cosas cambió con la publicación por parte de los matemáticos J. Kahn y G Kalai en el Bulletin of the American Mathematical Society de un artículo que se titulaba Un contraejemplo de la conjetura de Borsuk .(1)
Lo que Kahn y Kalai hicieron fue demostrar que el número de Borsuk para cualquier objeto n-dimensional crecía exponencialmente con la dimensión. Más concretamente demostraron que cuando la dimensión crece hacia infinito, el número de Borsuk tiende asintóticamente a una función exponencial, que resultó ser la función siguiente:
g(n)=(1,1) SQR(n)
donde SQR(n) quiere decir raíz cuadrada de n.
Una de las propiedades de las funciones exponenciales es que por muy despacio que avancen al principio ( y esta lo hace muy lentamente, pues la base es cercana a la unidad, y el exponente no es n , sino su raíz cuadrada), siempre terminan por superar a cuanquier función polinómica. Concretamente la función f(n)= (n+1) que proponía la conjetura de Borsuk es polinómica de grado uno.
Para un valor de n = 9.162 la función exponencial g(n)=(1,1) SQR(n) comienza a ser mayor que (n+1), luego a partir de ahí la conjetura de Borsuk debe fallar necesariamente.
Este resultado zanja la cuestión de la validez universal de la conjetura, pero deja abierta una incógnita bastante incómoda.
Efectivamente, tal valor de la dimensión (n=9.162) es una simple cota máxima de cumplimiento de la conjetura: asegura que de ahí hacia arriba se deja de cumplir, pero nada dice de valores menores que 9.162. Bien pudiera ser que falle desde valore bastante menores.
Las sucesivas cotas de d han ido bajando : Nilli obtuvo el valor de 946, Raigorodsky 561 y Weissbach el de 560. Más recientemente, ya en el año 2.000, Aicke Hinrichs alcanzó el valor de 323. El artículo está disponible aquí.
EN todo caso,el tema está abierto. ¿Cuál es el valor de la dimensión para el cual la conjetura de Borsuk empieza a ser falsa?
______________________________________________________
HACE UN AÑO comenzábamos una serie de tres post para responder la pregunta ¿Qué es un número?
Vimos que contra la opinión general el número no es un concepto primigenio en la matemática, sino que se basa en el concepto anterior de conjunto.
En este post comenzamos a ver los axiomas en los que nos íbamos a basar, aquí desarrollamos la idea y finalmente concluimos con la extraordinaria idea de que fundamentación de los números naturales y la matemática toda está basada en el conjunto vacío. A Siddharta Gautama el Buda le hubiera gustado esta idea.
______________________________________________________
(1) J. Kahn & G. Kalai: A counterexample to Borsuk's conjecture, Bulletin Amer. Math. Soc. 29 (1993), 60-62.
4 comentarios
Agnesi -
Me gustaría poder acceder al artículo, gracias.
Sun Nov 29 08:36:56 2015
(46.222.189.94)
Mozilla/5.0 (Windows NT 6.1) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/46.0.2490.86 Safari/537.36 http://tiopetrus.blogia.com/2005/013101-la-conjetura-de-borsuk-y-2-.php
Anónimo -
Adrian -
Adrian -
Por otro lado no es recomendable lo que hice yo poner una imagen de otro porque le robamos ancho de banda...
por otro lado para las formulas de los post te recomiendo MathML