Conceptos

Los grupos cíclicos

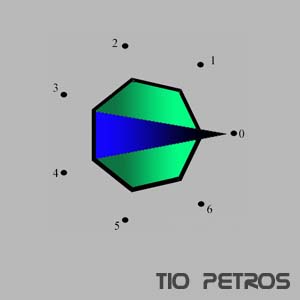
En el post anterior hemos presentado los números complejos de módulo unidad como operadores de giro sobre otros números complejos. Esta forma de verlos nos lleva a pasear por los llamados grupos cíclicos. Espero que sea un paseo agradable.

Supongamos que tenemos un selector de n posiciones, como el de la figura. El aparato está siempre en alguna de las n posiciones, y nosotros podemos actuar sobre él, girando la aguja hasta donde nos plazca (siempre hasta una de las n posiciones fijas).

Tenemos por tanto dos conjuntos perfectamente diferenciados, al conjunto de las posibles posiciones del selector, y el conjunto de las posibles acciones nuestras sobre el mismo. Llamaremos X al primero y G al segundo.

Está claro que el conjunto X tiene siete elementos en la figura, y n elementos en el caso general. Los representaremos con números naturales.

X={0,1,2,3,4,5,6}

Los elementos del otro conjunto no son posiciones según hemos dicho, sino nuestras acciones sobre el selector. Podemos girar a la izquierda, o a la derecha hasta la siguiente posición, o podemos girar k posiciones a la izquierda o a la derecha. Consideraremos acciones diferentes las que produzcan resultados diferentes, lógicamente. Esto quiere decir que efectuar un giro de una posición a la derecha es lo mismo que hacerlo de (n-1) posiciones en sentido contrario.

Así pues, el conjunto G también tiene n elementos, que denominaremos así:

G={g₀, g₁, g₂,..., g_n-1}

Donde g_i será el giro de i posiciones a la izquierda. (exactamente podría ser en sentido contrario, pero sucede que cuando un servidor debe elegir entre derecha e izquierda, pues eso; elige).

El conjunto G podría ser perfectamente el conjunto de las n raíces enésimas de la unidad del post anterior. No en vano adelantábamos allí que dichos números complejos podían entenderse como giros de una amplitud de la enésima parte de una vuelta, o cualquier múltiplo de esta cantidad.

Pues bien, este conjunto G es más que un conjunto. Es un grupo. Ahora explicaremos esto. Pero de momento diremos que este grupo actúa sobre el conjunto de estados X.

Esta actuación implica considerar loe elementos de G como operadores que afectan a los estados (elementos del conjunto X)

Así, g₁(0) ( el operador g₁ actuando sobre el estado 0) quiere decir el estado que tenemos cuando estando previamente en el cero hacemos un giro de una posición a la izquierda. Evidentemente g₁(0)=1. Es fácil ver la veracidad de las siguentes expresiones:

g₀(x) = x, para todo x € X

g₂(0) = 2

g₁ (g₂(0)) = g₁ (2) = 3

La primera igualdad nos dice que el giro nulo deja todo como estaba. La última supone la realización de un giro y luego otro. El resultado siempre se podría haber hecho de una sola vez mediante un giro único.

Efectivamente, existe una operación natural entre los elementos de G: g_i* g_j, que consiste simplemente en ejecutar ambos seguidos; primero el que escribimos a la derecha (g_j) y luego el otro (g_i).

Además, dado un giro concreto, siempre hay otro en G que deja las cosas como estaban. Diremos que cada elemento de G tiene un simétrico. Denotaremos g^-1 al elemento simétrico de g.

Queda una última propiedad, que permite agrupar giros por parejas sin alterar el orden en el que operan:

g_i* (g_j *g_k) = (g_i* g_j) *g_k)

Todo conjunto con una operación que tenga estas propiedades será llamado desde ahora un grupo .

Este grupo nuestro tiene unas propiedades adicionales que no satisfacen todos los grupos, ni mucho menos. Por ejemplo: uno sólo de sus elementos puede generar a todos los demás por simple composición consigo mismo. Esto quiere decir que a base de la única acción de girar una sola posición podemos generar todas las acciones del grupo. En lenguaje técnico diremos que G es finitamente generado, cuando todos los elementos son generados por composición de un grupo finito de ellos, y monógeno cuando lo son por uno solo de ellos , como en nuestro caso.

G =[ g₁]

Diremos que g₁ es un generador de G

Noten que hemos sustituido las llaves {} de los conjuntos por corchetes []. En la notación habitual se usan los signos “mayor y menor que”, pero me dan problemas porque Blogia los interpreta como comienzo de etiquetas HTML...

Llamaremos orden de un grupo G a su número de elementos, y escribiremos o(G)=n. Llamaremos orden de un elemento de G al orden del subgrupo generado por dicho elemento. Está claro que si y solo si dicho elemento g_k es un generador de todo G , entonces o(g_k)=n.

Llamaremos cíclico a un grupo tal que todos sus elementos son generados por uno solo. Es evidente que nuestro grupo de giros del conmutador es un grupo cíclico.

Basta por hoy. Terminamos con una pregunta tan sólo para aquellos que nada sepan de teoría de grupos:

Nuestro grupo completo es generado por uno sólo de sus elementos, lo hemos visto con el elemento más sencillo g₁, que es el menor giro posible a parte del nulo g₀, claro. El elemento nulo malamente puede generar nada distinto de sí mismo.

Pero ¿los demás?. ¿Es g₂ también un generador de G ?, ¿Y un g_k genérico? ¿Depende de algo que la respuesta sea positiva o negativa?

Les espero para continuar hablando de grupos cíclicos.

Las raíces de la unidad (2)

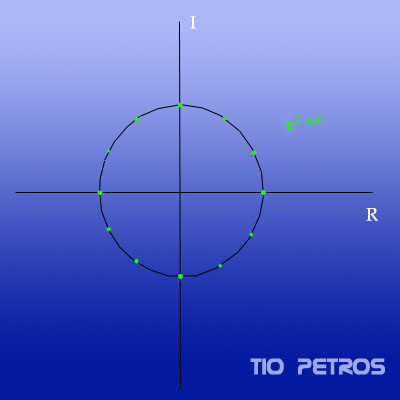
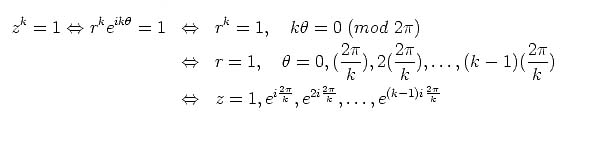Es muy notable que con los pocos conceptos desglosados en el post anterior se esté ya posibilitado para encontrar los k números complejos que satisfacen la ecuación:

z^k=1.

Más notable aún es la brevedad del desarrollo necesario para hacer tal cosa, tres renglones, como pueden ver en la ilustración que encabeza este post.

Sea z un número complejo raíz k-ésima de la unidad. Intentemos seguir paso a paso los tres renglones de la demostración:

Por su propia definición podemos poner:

z^k=1 Ecuación(1)

Pongamos tanto z como el 1 (que es un número complejo al fin y al cabo) en la forma exponencial (que llamaremos a partir de ahora forma polar) que aprendimos en el post anterior. z es un complejo genérico del que a priori nada sabemos, luego su forma será completamente general:

z=r·e^ix donde la x sustituye a la letra griega zeta, que no puedo reproducir aquí.

1= e^i·0

No tenemos más que sustituir ambos números en la ecuación (1) anterior, teniendo en cuenta que z^k tiene la forma:

z^k=(r·e^ix)^k =

r^k·e^ikx

Por tanto la igualdad (1) se convierte en:

r^k·e^ikx = e^i·0

El resto del desarrollo es pura aritmética, igualamos coeficientes y exponentes en ambos miembros y obtenemos el resultado que anunciábamos: las raíces k-ésimas de la unidad son k números complejos sobre la circunferencia unidad, y dividen a ésta en k partes iguales.

Lo vemos mejor en la ilustración siguiente, para k=7:



Cada punto es una rotación del anterior de un k-ésimo de vuelta, o sea, de 2PI/k radianes. Esta reflexión nos da un nuevo punto de vista de estos números complejos: no como números sino como operadores. Me explico.

Se tenemos un complejo en forma polar z=r·e^ix y lo “operamos” con e^iw multiplicando ambos, obtenemos lo siguiente:

z=r·e^ix· e^iw= z=r·e^i(x+w)

Esto es: obtenemos un nuevo punto que es el primitivo, pero girado un ángulo w en sentido contrario a las agujas del reloj. Así, podemos entender un complejo unitario (de módulo igual a uno) como una operación giro alrededor del origen de coordenadas. Esto será importante en el post siguiente, en el que hablaremos de grupos cíclicos.

Las raíces de la unidad (1)

Definir funciones en el campo complejo es relativamente fácil. El cuerpo C se define como el conjunto de pares de reales (a,b) con una operación suma y otra producto:

(a,b)+(c,d)=(a+c, b+d)
(a,b)·(c,d)=(ac-bd, bc+ad)

Aquí no hay nada arbitrario. Si bien podemos definir las operaciones queramos y luego comprobar si tenemos o no un cuerpo, la definición anterior corresponde a la idea previa de que existen números cuyo cuadrado es negativo: los números imaginarios. Es muy fácil comprobar que las definiciones de suma y producto anteriores son simplemente la expresión de que las partes reales e imaginarias se suman y multiplican algebráicamente teniendo en cuenta que i²=-1.

Ciertamente, para tener perfectamente construido el cuerpo C no hizo falta un alarde de imaginación y de genialidad como en el caso del cuerpo de los reales; hizo falta tan sólo la valentía de postular la existencia de pleno derecho de un “número” i cuyo cuadrado era –1. Todo lo demás viene dado una vez que se ha cometido esta audacia. Un número complejo es por tanto un par, en el que el primer elemento es un número real, y el segundo es un número imaginario, o sea: un real multiplicado por la i así definida. Podemos escribir dicho número en forma de par (a,b) o en forma de binomio a+bi.

Pues bien, resulta sencillo definir en C otras operaciones más complicadas, por simple extrapolación de sus definiciones en el caso real. Para ello suele ser muy conveniente utilizar las expansiones en forma de serie de potencias de las funciones elementales de R , y extrapolarlas a C .

Concretamente la función exponencial, que para un número real está definida así:



para un imaginario puro la definimos de la misma forma:



Quiero hacer hincapié en un hecho fundamental: no hemos utilizado, no vamos a utilizar ninguna propiedad desconocida para manejar, por primera vez en este blog los números complejos. A riesgo de ser repetitivo, diré una vez más que la única audacia cometida es postular la existencia del número i, cuyo cuadrado vale i²=-1.

Las sucesivas potencias de i son triviales:

i³=i· i²=-i
i⁴= i²· i²=(-1)·(-1)=1
i⁵= i⁴·i=i

y a partir de aquí se repite el ciclo.

Así pues, operando con los sucesivos términos de nuestra ecuación, obtenemos:



y ahora no tenemos más que dejarnos llevar por el instinto. Agrupamos los términos que llevan la i imaginaria por un lado y los que no la llevan por la otra, obteniendo:



Ahora resulta que ambos paréntesis son el desarrollo en serie de las funciones trigonométricas seno y coseno, cosa que no por no ser trivial, deja de ser cierta.

Así pues, la cosa queda así, obteniendo la archiconocida fórmula de Euler



Esto es fue una gran sorpresa. Las funciones trascendentes tales como las exponenciales y las trigonométricas eran viejas conocidas en tiempos de Euler, y todo el mundo sabía que las primeras son funciones de rápido crecimiento (crecimiento exponencial, traspasado al lenguaje cotidiano), mientras que las segundas reflejaban los vaivenes cíclicos de las oscilaciones de la naturaleza; las mareas, los péndulos... Qué quería decir esta fórmula increíble?

No tiene mucho sentido hacer cábalas sobre significados ocultos de esta bella ecuación, ni tiene sentido ver misticismos orientales en su particularización para x= pi; pero no deja de ser sorprendente esta relación, conocida como la fórmula de Euler

Nos servirá para expresar un número complejo de una tercera manera: en forma exponencial. Veamos las implicaciones de la fórmula en cuestión.

Dado que el módulo de un número complejo se obtiene por el teorema de Pitágoras, como pueden ver en la ilustración siguiente:



resulta claro que nuestro exponencial de imaginario puro es un complejo unitario, y que el valor x nos indica precisamente el ángulo que forma el eje X real con el vector que desde el origen apunta a dicho número complejo. Una vez más, nada nuevo hemos utilizado, sólo la conocida relación trigonométrica sin²2(x)+ cos²2(x)=1.

Así pues, e ^ix representa un número complejo que está situado a distancia uno del centro de coordenadas, y cuyo radio vector forma un ángulo x con el eje real. Es fácil comprender que si queremos representar en forma exponencial y complejo de módulo diferente de la unidad, bastará multiplicar su correspondiente unitario por el módulo, obteniendo

z= r· e ^ix

como expresión general de un complejo cualquiera.

Así, mientras x va recorriendo los valores reales desde 0 hasta 2·PI, z= e ^ix va recorriendo la circunferencia unidad centrada en el origen, girando en contra de las agujas del reloj. La fórmula mágica que surge al igualar x a 2·PI, y que ya la hemos usado alguna vez en este blog:



no representa ninguna conexión cósmico-mágica, ni tiene mística alguna en su interior,si la ponemos en forma menos críptica, así:



nos está diciendo que con un ángulo de PI radianes, estamos en el punto –1 del eje real, cosa que puede entender un niño ⁽¹⁾.

Ahora tenemos ya las herramientas para comprender que las raíces enésimas de la unidad , las soluciones de la ecuación

x ⁿ=1

surgen como bellas particiones de la circunferencia unidad. Lo vemos en el post siguiente, y luego pasearemos por los polinomios ciclotómicos. Les deseo un agradable paseo conmigo.

________________________________________________________________

(1) Un niño bastante listo, no un niño cualquiera.

Un cuerpo algebraicamente cerrado

Cuando el cuerpo de los números reales estuvo razonablemente bien construido como el conjunto cociente de todas las sucesiones de Cauchy de racionales con la relación de equivalencia apropiada, se consiguió una proeza. Se tenía ya rigurosamente construido un cuerpo arquimediano, ordenado y completo.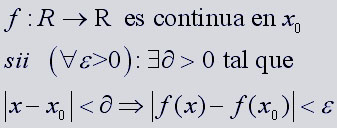

Sin embargo, en cierto modo el cuerpo R era decepcionante: una simple ecuación de segundo grado tal como ésta:

x ²+1=0

no tenía soluciones en él.

A nadie se le escapará que no estoy presentando las cosas cronológicamente: era de antiguo conocido que no existen soluciones reales de ecuaciones muy sencillas. Sin embargo el paso siguiente, que consistía en la construcción de un cuerpo algebraicamente cerrado en el cual todo polinomio de coeficientes racionales (o enteros, lo mismo da) tenga solución en su seno, estaba al alcance de la mano. De hecho, intelectualmente la construcción de R fue un reto mucho mayor que la construcción de C , el cuerpo de los números complejos, ya que este surge casi trivialmente con la consideración de pares ordenados (a,b) de números reales si definimos bien las operaciones suma y producto.

Tenemos así un cuerpo numérico algebraicamente cerrado, como nos lo enuncia el merecidamente famoso Teorema fundamental del álgebra , que dice que

todo polinomio a coeficientes complejos tiene un raíz compleja, es decir existe un número complejo donde el polinomio evalua a cero.

Esto es lo mismo que decir que todo polinomio de grado n con coeficientes complejos (o naturales, pues los naturales complejos son); tiene en C exactamente n soluciones, no necesariamente diferentes.
Efectivamente, si P_n(x) es el polinomio original, el enunciado del teorema asegura la existencia de una raíz w, con lo que podemos expresar el polinomio como:

P_n(x) =(x-w)·P_n-1(x) .

Ahora aplicando lo mismo al nuevo polinomio con un grado menos P_n-1(x) y sucesivamente hasta llegar al polinomio de grado uno, tenemos n raíces, no necesariamente diferentes de P_n(x) en el seno de C .

Particularmente, la ecuación

x ⁿ=1

tiene n soluciones en C , ésta vez todas diferentes. Se trata de las denominadas raíces de la unidad .

El estudio de las mismas es una bella y multidisciplinar parcela de la matemática que es: la teoría de variable compleja , la geometría, la teoría de grupos cíclicos y la teoría de polinomios ciclotómicos beben de esta fuente de cristalinas aguas.

De ello nos ocuparemos en los próximos posts.

Me parece una buena manera de iniciar el año. Espero que a ustedes también.

Continuidad

La ciencia se puede aprender de memoria, pero la sabiduría no.

Laurence Sterne
(1713-1768) Novelista británico

Miren la ilustración que encabeza el post.

Este galimatías suele ser el primer encuentro de un estudiante de bachiller (o como lo quieran llamar ahora, porque sólo los profesionales del ramo saben cómo coño se denominan en cada momento los estudios que cursan los adolescentes)...decía que este aparente galimatías suele ser el primer encuentro de un chaval con la matemática de verdad.

Dicho encuentro es invariablemente traumático. Y la verdad es que parece mentira que tras estas cadenas de símbolos se encuentre tanta sutileza, tanta belleza y tanta historia.

No es por casualidad que hablamos de ello ahora. Si el lector ha seguido los últimos post, aunque nada supiera del tema tiene las herramientas conceptuales necesarias para hacer muchas cosas interesantes.

Como en otras ocasiones, detrás de estos símbolos están ideas topológicas mucho más profundas que las que sospechan los estudiantes de BUP.

El hecho de que tantos estudiantes se hayan estrellado contra estos dos renglones, poniendo ojos como platos y decidiendo aprenderlos de memoria, como única alternativa a la locura es doblemente penoso. Por un lado, todas las grandes ideas son muy sencillas, y esta también lo es; por otro lado, sin entender BIEN esto, poco análisis matemático se puede comprender realmente. Y créanme que sé de lo que hablo: durante años estuve dando clases particulares a chavales y bien raro era encontrarse con alguno que supiera exactamente qué significaba todo esto.

Esta definición es la superación de la fase intuitiva en el cálculo. La mayoría de edad de la matemática, debida a inmensos cerebros que se llamaron Cauchy, Weierstrass, y un largo etcétera. Es una expresión estática, sin frases vagas del tipo " cuando la x tiende a tal cosa" o " cuando tal distancia se hace infinitamente pequeña ". Es estática como estático es un cristal natural perfecto o una obra de arte escultórica.

Como es tan importante, y no tenemos prisa, le dedicaremos varios post. Al final, nos parecerá tan clara como si estuviera escrita en castellano; y si no es así, será exclusivamente por mi culpa.

Hasta la semana que viene.

Continuidad

La ciencia se puede aprender de memoria, pero la sabiduría no.

Laurence Sterne
(1713-1768) Novelista británico

Miren la ilustración que encabeza el post.

Este galimatías suele ser el primer encuentro de un estudiante de bachiller (o como lo quieran llamar ahora, porque sólo los profesionales del ramo saben cómo coño se denominan en cada momento los estudios que cursan los adolescentes)...decía que este aparente galimatías suele ser el primer encuentro de un chaval con la matemática de verdad.

Dicho encuentro es invariablemente traumático. Y la verdad es que parece mentira que tras estas cadenas de símbolos se encuentre tanta sutileza, tanta belleza y tanta historia.

No es por casualidad que hablamos de ello ahora. Si el lector ha seguido los últimos post, aunque nada supiera del tema tiene las herramientas conceptuales necesarias para hacer muchas cosas interesantes.

Como en otras ocasiones, detrás de estos símbolos están ideas topológicas mucho más profundas que las que sospechan los estudiantes de BUP.

El hecho de que tantos estudiantes se hayan estrellado contra estos dos renglones, poniendo ojos como platos y decidiendo aprenderlos de memoria, como única alternativa a la locura es doblemente penoso. Por un lado, todas las grandes ideas son muy sencillas, y esta también lo es; por otro lado, sin entender BIEN esto, poco análisis matemático se puede comprender realmente. Y créanme que sé de lo que hablo: durante años estuve dando clases particulares a chavales y bien raro era encontrarse con alguno que supiera exactamente qué significaba todo esto.

Esta definición es la superación de la fase intuitiva en el cálculo. La mayoría de edad de la matemática, debida a inmensos cerebros que se llamaron Cauchy, Weierstrass, y un largo etcétera. Es una expresión estática, sin frases vagas del tipo " cuando la x tiende a tal cosa" o " cuando tal distancia se hace infinitamente pequeña ". Es estática como estático es un cristal natural perfecto o una obra de arte escultórica.

Como es tan importante, y no tenemos prisa, le dedicaremos varios post. Al final, nos parecerá tan clara como si estuviera escrita en castellano; y si no es así, será exclusivamente por mi culpa.

Hasta la semana que viene.

Marea roja

Varias veces he dicho que además del pensamiento crítico y de la matemática, la belleza tiene su cabida en este blog. Hagamos un alto, aunque sea para llamar la atención sobre una de las maravillas que está ocurriendo ahora mismo muy cerca de todos nosotros.

Ocurre todos los años, pero no por eso deja de ser maravilloso.



Comienza por las puntas allá por septiembre, las hojas más altas se vuelven rojas, y el resto del árbol parece no darse cuenta.

Sin embargo, poco a poco es como si una pintura bermellón se deslizara hacia abajo,en octubre ha llegado a la mitad del árbol



al llegar mediados de noviembre ha invadido todo el árbol.

Dentro de quince días estará a reventar, lleno de sangre como anunciando la inminencia de una explosión de vida… y sin embargo seguidamente las hojas caerán una a una, se retirará la sabia y se dormirá hasta la primavera.

Marea roja

Varias veces he dicho que además del pensamiento crítico y de la matemática, la belleza tiene su cabida en este blog. Hagamos un alto, aunque sea para llamar la atención sobre una de las maravillas que está ocurriendo ahora mismo muy cerca de todos nosotros.

Ocurre todos los años, pero no por eso deja de ser maravilloso.



Comienza por las puntas allá por septiembre, las hojas más altas se vuelven rojas, y el resto del árbol parece no darse cuenta.

Sin embargo, poco a poco es como si una pintura bermellón se deslizara hacia abajo,en octubre ha llegado a la mitad del árbol



al llegar mediados de noviembre ha invadido todo el árbol.

Dentro de quince días estará a reventar, lleno de sangre como anunciando la inminencia de una explosión de vida… y sin embargo seguidamente las hojas caerán una a una, se retirará la sabia y se dormirá hasta la primavera.

La [conjetura / teorema] de [Poincaré / Poincaré-Perelman]

Como ya dijimos en alguna ocasión una conjetura es un teorema al que le falta la parte más interesante: la demostración. Dicho de otro modo: una conjetura nada tiene que ver con un teorema; es una simple afirmación. Aunque a veces se pervierta la nomenclatura, como en el caso del “Ultimo teorema de Fermat”, que no tuvo tal rango hasta que Wiles lo demostró hace pocos años.

Visto así, parece que una conjetura tiene poco valor, y es poco más que una opinión. Así es en parte, de hecho muchas conjeturas resultaron falsas a la postre. Sin embargo normalmente tienen el valor de ser agudas observaciones realizadas por especialistas, retos lanzados al mundo para que las mejores mentes del planeta se esfuercen en desentrañar sus misterios. Así ocurre con una de las más famosas: la Conjetura de Poincaré

Pasamos a explicar en qué consiste la conjetura, tan de moda últimamente a raíz de la demostración (pendiente de refrendar por lo que yo sé, pero probablemente correcta) del matemático ruso Grigory Perelman

La Conjetura de Poincaré es una afirmación topológica. Una vez explicamos aquí que la topología tiene un estatus muy especial dentro de la matemática. Supondremos que el lector sabe qué estudia la topología por tanto.

A veces, los matemáticos tienen algo de naturalistas; taxónomos más concretamente. Les gusta clasificar cosas y ponerles etiquetas. Este gusto es totalmente lógico; para clasificar atendemos a las propiedades más esenciales de las cosas e investigamos la diversidad de las mismas. El procedimiento básico suele ser el siguiente: se establecen relaciones de equivalencia entre los objetos; no relaciones cualesquiera, sino relaciones que se consideran relaciones importantes precisamente porque atienden a propiedades que consideramos esenciales de las mismas. Dichas relaciones inducen clases de equivalencia dentro de las cuales todos los objetos están “emparentados”, y estudiamos el conjunto cociente de clases obtenido. Ese es el esquema esencial de clasificación en matemáticas, si bien su aplicación práctica puede variar, y así se han establecido clasificaciones para los grupos simples finitos, para las superficies en R ⁿ , las formas cuadráticas, los grupos de Lie, etc, etc.

La relación más habitual que se emplea en topología es la relación “ser homeomorfo” . Pocas veces se ha escondido detrás de una palabra tan fea un concepto tan bello. Dado un espacio de trabajo X, dos objetos A y B de dicho espacio (dos subconjuntos de “puntos” de X) son homeomorfos si pueden transformarse el uno en el otro mediante una transformación continua especial llamada homeomorfismo. Diremos que una aplicación de A a B es un homeomorfismo si es biyectiva, continua e inversible, siendo su inversa igualmente continua. Dado que si A y B son homeomorfos, entonces para un topólogo “son” esencialmente el mismo objeto, se comprende la importancia de la clasificación atendiendo a tal concepto.

Pues bien; la capacidad simplificatoria de este procedimiento es impresionante: al tratar a todos los objetos de cada clase como uno sólo (su representante canónico), obtenemos un panorama mucho más racional del universo que estamos estudiando. Es de esperar (de hecho, está asegurado) que todos los objetos de una misma clase de homeomorfia exhiban las mismas propiedades topológicas.

El problema es que lo que vale para un espacio topológico no tiene porqué valer para otro. Dado que un espacio de tres dimensiones no es homeomorfo a uno de siete, cabe esperar que ciertas cosas (cosas topológicas, entiéndanme) que ocurran en un universo de tres dimensiones no ocurrirán o al menos no tienen porqué ocurrir en otro de siete, y viceversa. Y aquí está el quid de la cuestión en lo que a la Conjetura de Poincaré se refiere.

Pero vayamos con calma.

Consideremos una esfera. Es muy importante explicar que entendemos que una esfera es el conjunto de puntos del espacio que equidistan de otro, llamado centro. Esto viene a cuento porque con esta definición una esfera es una superficie. No una bola maciza sino la superficie que la delimita. Esto es básico para entender lo que sigue. Para dejar más claro el asunto, la llamaremos 2-esfera por ser un objeto bidimensional, aunque esté inmerso en un espacio de tres dimensiones.


Todo objeto homeomorfo (topológicamente equivalente) a una esfera tendrá las mismas propiedades topológicas que una esfera; esto es una perogrullada. Lo que no lo es es preguntarse si una determinada colección de propiedades de la esfera es una caracterización topológica de la misma. Esto no es nada trivial. Y de eso va la conjetura.

Una caracterización es un conjunto de propiedades que definen sin ambigüedad un objeto. Tres propiedades topológicas son importantes en una esfera:

1.- Es compacta
2.- Es orientable
3.- Es simplemente conexa

Hace mucho tiempo que quedó claro que este conjunto de tres propiedades es una caracterización de una 2-esfera, pero ¿qué ocurre en dimensiones superiores?

Una 3-esfera NO ES una esfera maciza, como alguno podría pensar. Una 3-esfera es una variedad diferenciable de tres dimensiones, que podemos definir como el conjunto de los 4-puntos de R⁴ que equidistan de uno dado (centro). Es una 3-variedad inmersa en un espacio de 4 dimensiones, por tanto.

Pues bien; ¿sigue siendo el conjunto de las tres propiedades una caracterización de las 3-esferas?

La Conjetura de Poincaré afirma que para cualquier número de dimensiones el conjunto de las tres propiedades es en efecto una caracterización de las n-esferas.

Apreciar el sabor de este bello (bellísimo, no lo duden) postulado es la tarea que les proponga en sucesivos post, en los que desgranaremos conceptos topológicos, y recorreremos la historia de la conjetura hasta llegar al bueno de Grigory Perelman , que se encerró durante años hasta dar con una demostración de este reto que el genial Poincaré lanzó a sus iguales.

Seguiremos disfrutando (yo al menos) con este tema en días sucesivos. Les espero.

Indices de poder

En el post anterior vimos que cuando los votantes en una decisión de aceptación o rechazo de una propuesta tienen pesos específicos diferentes derivados del número de votos o escaños en el caso de un parlamento, del número de acciones en el caso de una asamblea general de accionistas o de cualquier otro tipo, el poder real que poseen no es proporcional a dichos pesos como sería de desear si atendemos al ideal de justicia por el cual tal proporcionalidad debiera darse. En este pos veremos la forma de calcular el poder real de los integrantes, y comprenderemos que, a veces, dicho poder es muy diferente del que las urnas, o el número de acciones les debieran proporcionar.

Para ello vamos a desarrollar un poco la teoría de los sistemas de votación ponderados, donde cada votante tiene un peso específico propio. Nada mejor que empezar unificando la nomenclatura:

Llamaremos v₁, v₂,..., v_n a los votantes, siendo w₁, w₂,..., w_n la importancia, el peso o el número de votos de cada uno de ellos. Llamaremos q a la cantidad de votos necesarios para aprobar una propuesta. Debe quedar claro que llamamos votante a cada grupo de poder, no a cada miembro de dicho grupo de poder. En el caso de un parlamento, los votantes serán los partidos, y el peso específico de cada partido será el número de escaños del mismo.

De ésta manera, el problema de votación ponderado queda perfectamente definido, y lo representaremos así:

V=[q; w₁, w₂,..., w_n].

Llamaremos Coalición a un conjunto de votantes que se han unido para votar a favor o en contra de una propuesta. Si admitimos como coalición las unitarias (formadas por un solo votante) hay tantas coaliciones como subconjuntos de votantes. Su número es de 2 ⁿ.

Una Coalición ganadora es una coalición en la que la suma del número de votos de sus miembros es superior o igual a la cuota q .

Una coalición de bloqueo es aquella en la que la suma del número de votos de sus miembros es suficiente para bloquear (conseguir que no se apruebe) una propuesta. En evidente que tal coalición debe tener un número de votos superior al total menos la cuota de aceptación q .

¿Cómo podemos medir el poder real de un miembro? Está claro que no sirve estimar las posibilidades que tiene para formar parte de una coalición ganadora. Esto es así porque pudiera ser que dicha coalición fuera ganadora sin necesidad de su apoyo, en cuyo caso es indiferente su adhesión a la misma. Para acercarnos al concepto que necesitamos introduciremos una idea auxiliar: el swing.

¿Qué es un swing?

Un swing para un votante i con peso específico w_i es un par de coaliciones (S U{i}, S ), de forma que S U{i} es una coalición ganadora y S es una coalición perdedora. Dicho de otro modo: un swing del votante i es una coalición en la que el votante i es un votante basculante : votante que si se retira de una coalición ganadora, deja de serlo.

Llamaremos N_i al número de swings del votante i, y N a dicha cantidad extendida a la totalidad de votantes:

N= N₁+ N₂+...+ N_n

Parece lógico interpretar que el número de swings de un votante es un buen índice del poder real del mismo: existen N_i posibles coaliciones en las cuales su adhesión resulta determinante. Denominaremos Indice de poder de Banzhaf normalizado del jugador i-ésimo a la cantidad

B_i= N_i/N

Veamos un ejemplo:

En una determinada empresa hay presentes cuatro accionistas. A,B,C y D, con el siguiente capital invertido en la misma, (en millones de euros por ejemplo): 13, 12, 6 y 2 . Las decisiones se aceptan por mayoría simple: basta reunir un peso de 17.

Calculemos índice de poder de Banzhaf normalizado de cada uno de ellos. Empezaremos por calcular el peso específico de cada una de las posibles coaliciones. En la figura aparecen en negrita aquellas que igualan o sobrepasan la cuota q=17.



Tengamos ahora en cuenta las coaliciones S para las cuales i es determinante aquellas en las que siendo S perdedora, S U{i} es ganadora:



Por tanto, podemos ver que el número de swings totales es 12, y los de cada accionista son:

N₁= 4
N₂= 4
N₃= 4
N₄= 0

Y por lo tanto el Indice de Banzhaf de cada uno valdrá:

B₁= 4/12=1/3
B₂= 4/12=1/3
B₃= 4/12=1/3
B₄= 0

El poder se reparte equitativamente entre los tres primeros, quedando el cuarto sin cuota alguna de poder. El resultado, como pueden ver, no respeta proporcionalidad alguna: el tercer accionista tiene menos de la mitad de derechos que el primero, resultando con una cuota de poder igual. Pero es la situación para el grupo minoritario, que queda sin poder alguno.

Las cosas pueden ser aún más injustas: examinen si les apetece la situación en un gobierno con tres partidos A,B,C con el 49% , el 49% y el 2% de escaños respectivamente.

Otra situación curiosa se da para el caso de cuatro partidos con el 26%,26%,26% y 22%.

Que pasen un feliz fin de semana.

Poder efectivo

En cierto modo, los números reales son más sencillos que los enteros. Esta afirmación parecerá algo absurda, teniendo en cuenta que los reales se construyen a partir de los racionales, éstos a partir de los enteros y éstos a partir de los naturales.

Me explico: la gran ventaja de los números reales es doble: por un lado, forman un cuerpo con las operaciones habituales, lo cual quiere decir que siempre es lícito sumar, restar, multiplicar o dividir dos reales entre sí: el resultado es otro número de la misma clase (salvo la división entre cero, que es anatema y cosa muy prohibida). La otra ventaja es que ese cuerpo es completo: esto quiere decir que “no tiene huecos”: todo número comprendido entre dos reales es asimismo real. (Técnicamente un cuerpo completo es aquel para el cual toda sucesión de Cauchy converge a un número que pertenece al cuerpo, pero esa es otra cuestión.)

¿Tiene esto alguna aplicación práctica? ¿Se ve en algún ejemplo que trabajar con números naturales puede ser más complicado que hacerlo con reales?

Pues sí. Y además los ejemplos son de una cotidianeidad apabullante. Cuando queremos repartir proporcionalmente a algunos valores dados un cierto número de premios entre personas, y esos premios no se pueden partir, empiezan los problemas. Lo vemos continuamente en las elecciones: los escaños no se pueden partir, de modo que es imposible hacer corresponder un determinado número de votos obtenidos con un escaño logrado, y mantener esta relación hasta efectuar el reparto completo: hace falta salirse de la norma para repartir los restos, y esto hace que el problema sea no sólo difícil, sino además muy cuestionable al existir varias soluciones no equivalentes.

Lo mismo ocurre cuando hay que efectuar una votación para aprobar o rechazar una propuesta, y cada uno de los votantes tiene un peso específico concreto: por ejemplo, votaciones en el congreso para aprobar una ley, donde existen N partidos , y el partido i tiene n_i escaños. El poder real de cada partido es la capacidad para influir en el resultado de aceptación o rechazo de la propuesta, y lo más justo es que dicho poder fuera proporcional al número de escaños, número que será aproximadamente proporcional al número de votos conseguidos. Así, el ideal democrático parece preservarse, y realmente son los ciudadanos los que aceptan, por delegación, o rechazan las propuestas. Sin embargo todo esto no es más que una bonita teoría que nada tiene que ver con la realidad. La realidad es que un partido en el congreso, un grupo de accionistas en una asamblea general, o un país en el seno de un organismo internacional puede tener una cuota de poder totalmente desproporcionada (a veces a favor, y otras en contra) a lo que debiera, entendiendo que “debiera” tener una cuota de poder proporcional a sus méritos: al número de escaños en el caso del partido en un congreso o al número de acciones en el caso del grupo de accionistas.

Si les parece, veremos la explicación de porqué esto es así, y veremos unas medidas de poder real creadas expresamente para la ocasión. Como habrán intuido, las causas de la desproporcionalidad real entre méritos y poder efectivo son matemáticas. En el fondo derivan de la dificultad intrínseca de trabajar con números enteros que mencionábamos al inicio, y las iremos viendo en post sucesivos. Espero que les parezca interesante este paseo que les propongo.

Recurrencia de Catalán

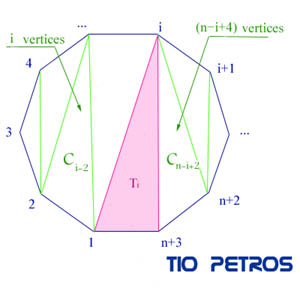Vamos a obtener la fórmula de recurrencia de los números de Catalán. Para ello, fijemos la nomenclatura: C_n es el número de triangulaciones con n triángulos, o lo que es lo mismo, de un polígono convexo de n+2 lados. Visto de otra forma: un polígono con i lados tendrá C_i-2 triangulaciones posibles.

Dado que el mínimo polígono existente tiene 3 lados, y se trata del triángulo, con una única triangulación (valga la redundancia y nunca mejor dicho), tenemos que C₁=1. Haremos C₀=1, como caso inicial.

Supongamos conocidos los valores de los primeros C_n.Intentaremos hallar C_n+1. Esto equivale a suponer conocidas las triangulaciones de polígonos hasta (n+2) lados e intentar conocer las del polígono de (n+3) lados.

Sea P un polígono de (n+3) lados, que numeraremos 1,2,3,…,n+2,n+3. Elegimos uno de los lados, el que tiene como vértices {1,(n+3)}. Una vez elegido este lado, tomamos uno de los vértices restantes (que llamaremos vértice i ) para formar un triángulo. (En rosa, el triángulo T_i en la figura). Dicho triángulo divide al polígono P en tres partes: un subpolígono P₁de vértices {1,2,3,…,i}; el propio triángulo T_i y otro subpolígono P₂ de vértices {i,i+1,i+2,…n+2,n+3}.

P₁ tiene obviamente i vértices. P₂ tiene (n-i+4) vértices. Esto quizás no es tan fácil de ver. Se comprende mejor al ver que la suma de los vértices de P₁ y P₂ debe ser una unidad superior a los vértices de P, puesto que el vértice i lo tomamos dos veces, una para cada subpolígono. Así pues deben sumar entre ambos (n+4) vértices, y por lo tanto P₂ tendrá (n-i+4) vértices.

Sabiendo el número de vértices de P₁ y P₂, sabemos automáticamente sus respectivos números de triangulaciones: C_i-2 y C_n-i+2 respectivamente. Luego para el triángulo T_i escogido tenemos C_i-2 .C_n-i+2 posibles triangulaciones.

Resulta que el vértice i lo podemos elegir desde i=2 hasta i=(n+2) para formar el triángulo T_i, luego tendremos tenemos que las posibles triangulaciones del polígono P, de (n+3) lados será dicho producto C_i-2 .C_n-i+2 extendido a todos los posibles valores de i:

Esto es:

C_n+1=C₀ C_n+ C₁ C_n-1+ C₂ C_n-2+…+ C_n-2 C₂+ C_n-1 C₁+ C_n C₀

Que es la fórmula de recurrencia deseada.

Dado que conocíamos los primeros casos:

C₀=1
C₁=1
C₂=2 triangulaciones de un cuadrado

Ahora podemos fácilmente ir hallando los siguientes:

C₃=1.2+1.1+2.1=5 triangulaciones de un pentágono
C₄=1.5+1.2+2.1+5.1=14 triangulaciones de un hexágono,… etc.

Los números de Catalán

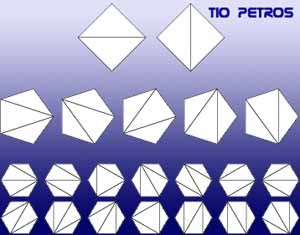La combinatoria es una de las ramas más arduas de la matemática (al menos desde mi humilde entender). No es otra cosa que el arte (o la técnica) de contar. Conforme se va complicando lo que queremos contar, es lógico que se vaya complicando proporcionalmente la forma de contarlo. Sin embargo, a veces la complicación es muy grande cuando lo que contamos no es tampoco nada del otro mundo. Me explico: en este momento tratamos de contar triangulaciones de polígonos, que supondremos regulares, o al menos convexos.

Una triangulación de un polígono es una partición del mismo en triángulos disjuntos cuyos vértices coinciden con los vértices del polígono. En la figura pueden ver todas las posibles triangulaciones de un cuadrado, un pentágono y un hexágono. Denominaremos C _n al número de posibles triangulaciones diferentes de un polígono utilizando n triángulos.

Si el polígono en cuestión tiene m lados, necesitaremos m-2 triángulos para hacerlo. En efecto, es fácil convencerse de esto comprobando que sólo dos de los triángulos comparten dos lados con el polígono, y todos los demás comparten necesariamente un lado tan sólo. Por tanto, C _n denotará tanto el número de triangulaciones de un polígono para el que se necesitan n triángulos, como el número de triangulaciones de un polígono de un polígono de n-2 lados.

En la figura se muestra que C ₂=2; C ₃=5 y C ₄=14.

El lector puede intuir que el procedimiento de contar exhaustivamente todas las triangulaciones deja de ser factible enseguida: debemos encontrar atajos, y en la búsqueda de atajos es donde se expresa el genio matemático, porque contar de uno en uno lo sabemos hacer todos, y no tiene gracia alguna.

Estudiaremos la recursividad de la sucesión de Catalán C ₀, C ₁, C ₂,...en la que obviamente C ₁=1, C ₂=2, y haremos C ₀=1.

Este método de encontrar los valores de C _n basándonos en valores anteriores, que se consideran ya conocidos es el método de recurrencia que ya explicamos en su día.

El conocimiento de la fórmula de recurrencia de una sucesión no nos ofrece simplemente la posibilidad de encontrar más fácilmente los elementos de la sucesión: también nos dice muchas cosas más. Por ejemplo: si demostramos que varios problemas de conteo, aparentemente dispares obedecen a la misma ley de recurrencia, hemos demostrado que en ambos problemas subyace el mismo concepto matemático. En el caso que nos ocupa, el de los números de Catalán (1), se han encontrado hasta 66 problemas geométricos de conteo accesibles mediante dichos números.

Lo vemos en el siguiente post.

____________________________________________________________________

Así denominados en honor a Eugene Catalán (1814,1894), matemático belga.

Calculando el origen de los días julianos

Continuando con lo prometido, efectuaremos el cálculo de la fecha de origen del sistema de cómputo temporal conocido como días julianos. Este post tiene interés para quien desee llegar hasta el final y es un mero desarrollo matemático. No es el post típico en´TioPetros.

Por facilidad de notación sustituiré el signo de las congruencias (los tres guiones) por el símbolo “:=”

Tenemos el siguiente sistema:

x := 20 mod 28 (congruencia 1)
x:= 0 mod 19 (congruencia 2)
x := 13 mod 15 (congruencia 3)

De la ecuación (1), tenemos x=20+28k con k entero.

Introduciendo en la segunda este último valor, tenemos:

20+28k := 0 mod 19
1+9k := 0 mod 19
9k := 18 mod 19

y por lo tanto:

k := 2 mod 19

Luego k=2+19s, para algún s entero.

Así pues x = 20+28k = 20+28(2+19s) = 76+532s, que introducido en la congruencia (3), da:

76+532s := 13 mod 15 , o simplificando

1+7s := 13 mod 15
7s := 12 mod 15
s := 6 mod 15 , lo que significa que

s=6+15t

Volviendo a reemplazar en el valor de x, obtenemos:

x=76+532(6+15t)=3268+7980t

Por lo tanto hemos obtenido que x := 3268 mod 7980

Así pues, el año buscado debe ser congruente con 3268 módulo 7980. Como el año 3268 está en el futuro, tomamos como origen el anterior congruente con él, que es el año 3268-7980=-4712.

Dado que en nuestro sistema de cómputo el año cero no existió, el año –4712 corresponde al año 4.713 a.C. .

Así pues, el 1 de Enero del año 4.713 antes de Cristo es el momento de origen del sistema de cómputo de tiempos conocido como días julianos.

El calendario (4)

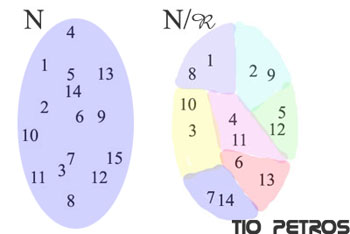Hemos comentado en posts anteriores que el concepto de congruencia era imprescindible en este estudio, vayamos con él:

CONGRUENCIAS

Supongamos que tenemos el conjunto N de todos los números naturales. Tomemos un natural cualquiera, por ejemplo el siete. Cuando dividimos por siete, el resto de la operación es un número comprendido entre 0 y 6. Pues bien, vamos a asociar a cada número natural el resto de su división por siete. Y ahora agrupamos los naturales en siete compartimentos; según los restos de la división realizada.

Esto que hemos hecho es establecer una relación de equivalencia (reflexiva, simétrica y transitiva). Todo número da el mismo resto al dividir por siete que sí mismo, si a da el mismo resto que b , entonces b lo dará igual que a , y si a da el mismo resto que b , y b da el mismo resto que c , entonces a dará el mismo resto que c . Cuando una relación tiene estas tres propiedades, se denomina de equivalencia, y cristaliza el conjunto original en una serie de compartimentos estancos dentro de cada uno de los cuales están todos los elementos relacionados entre sí, y solamente entre sí.

Estos compartimentos se denominan clases de equivalencia, en nuestro caso clases de restos módulo 7 , y clases de restos módulo p en el caso general. El conjunto de las siete clases se denomina conjunto cociente por la relación dada, y es un conjunto con p elementos(7 en el ejemplo que nos ocupa) , cada uno de los cuales es una clase, cada una de las cuales tiene dentro los elementos originales. Dicho conjunto cociente se denota N/R, siendo R la relación de equivalencia que hace cristalizar el conjunto original en clases, y en nuestro ejemplo concreto, se denominará N/p: conjunto cociente de clases de resto módulo p. Cada clase se expresa poniendo entre corchetes uno cualquiera de sus elementos; así en nuestro conjunto cociente de restos módulo 7, se cumple que [1]=[8]; la clase del 1 y la del 8 son la misma (lo cual es normal, dado que el 1 y el 8 son congruentes módulo 7.

Dos elementos que pertenecen a la misma clase, se denominan congruentes módulo p. En nuestro caso, vemos que el 9 y el 2 son congruentes módulo 7. Los números 16, 23,30, 37,...(7k+2),... también son congruentes módulo 7 con el 2 y el 9. Efectivamente, todos ellos dan un resto de 2 al dividir por 7. Cada clase de restos módulo p es representada por uno de sus elementos, normalmente el más pequeño, que se denomina el representante canónico de la clase. Así, el 1 es el representante de la clase [1],

La frase Los números a y b son congruentes módulo p se escribe de la siguiente manera:



Aunque en sentido estricto no lo son, podemos trabajar con las congruencias como si de ecuaciones se tratara, e incluso podemos formar sistemas de congruencias, de esta forma:



El teorema chino del resto nos da las pautas para saber cuándo un sistema de este tipo tiene solución. En efecto, aunque estamos acostumbrados a decir que un sistema de n incógnitas necesita n ecuaciones para tener solución, las cosas son más complicadas. El Teorema de Rouché-Frobenius da las condiciones suficientes y necesarias para que tal cosa ocurra, pero de ello ya hablaremos en otra ocasión. Baste decir que el teorema chino del resto nos dice que un sistema de congruencias como el anterior tiene solución si los módulos p ₁, p ₂,..., p _n son primos entre sí dos a dos. Esto quiere decir que tomando dos de ellos cualesquiera, no existe ningún número que divida exactamente a ambos, salvo la unidad.

Cuando esto ocurre, el sistema tiene solución única módulp p ₁x p ₂x...x p _n.

Si lo piensan un poco, esto es lo esperable. Pero si no les apetece pensarlo, hablaremos de ello en otro momento.

Por ahora, el lector se preguntará qué relación tiene esto con los días julianos.

Pues bien: hemos dicho que Scaliger quería encontrar un origen para su sistema; un año x en el pasado que fuera a la vez inicio de los tres ciclos.

Scaliger sabía que el año 1.560 tenía 1 como número del ciclo solar. También sabía que el año 532 fue el que Dionisio el Exiguo introdujo el sistema del ciclo lunar, y que tenía dicho año número áureo igual a 1. Sabía asimismo que el ciclo fiscal de indicción romana se instituyó el año 313 por Constantino, con lo que dicho año tenía número 1 en su correspondiente ciclo.

Los tres ciclos tienen módulos 28,19 y 15 respectivamente, luego el año inicial buscado deberá ser congruente con las tres fechas citadas vía sus respectivos módulo(pues cada uno de ellos era el primero de su correspondiente ciclo). Esto es:



Simplificamos este sistema: lo explico para la primera congruencia: 1560 es congruente módulo 28 con muchos números. Si los ordenamos todos, veremos que están separados 28 unidades cada uno del siguiente, porque estamos trabajando en módulo 28. Se trata de encontrar el más bajo congruente con 1560. Esto se hace buscando el múltiplo de 28 más cercano a 1560 por debajo, que es 55x28=1540. Como nos faltan 20 para llegar a nuestro 1560, resulta que 20 es el número buscado, congruente con 1.560 módulo 28. Luego podemos sustituir 1560 por 20 en la primera congruencia, sin variar el contenido de la misma.


Espero que el lector se de cuenta de que esta simplificación no es otra cosa que sustituir los números 1560,532 y 313 por los representantes canónicos de sus clases respectivas.

En definitiva, obtenemos:



Tenemos suerte: los tres módulos son primos entre sí por parejas, luego el Teorema Chino del resto es de aplicación:

Lo haremos pormenorizadamente en el próximo post, que será un mero desarrollo de los cálculos, por aquello de que lo hemos prometido. Así pues, el siguiente post sólo tendrá interés para los que quieran llegar hasta el final; el resto, simplemente puede obviarlo.

El calendario (3)

Centrémonos en el problema, porque no hay mejor manera de entender un método que saber qué problema se intenta solucionar con el mismo. Un astrónomo calcula el paso de un nuevo cometa por su punto más cercano al sol (perihelio) en el presente, demuestra que dicho cometa tiene una órbita periódica, y calcula su período en una unidad de tiempo, digamos en segundos. Obtiene 4.016.131.200 segundos. Es natural saber cuándo vamos a poder ver el cometa de nuevo. Hasta qué fecha de nuestro calendario hay que esperar?

Es del todo claro que no está nada claro. Incluso si cambiamos de unidad de tiempo, a días (46.483) la cosa está igual de oscura. Pasando a años ya tenemos algo más de claridad (127,35), pero empiezan las pegas: unos años tienen 356 días, y otros 366. Ya no está nada claro qué quiere decir 127.35 años, pues lo hemos obtenido dividiendo el número de días que teníamos entre 365.

Cuando mayor sea el lapso de tiempo que estamos midiendo, peor se nos pone la cosa. Es difícil saber a qué día corresponde una fecha de X días en el futuro cuando X es muy grande!

Para solucionar estos problemas, Joseph Justus Scaliger propuso en 1.583 un nuevo calendario de uso para astrónomos, en el que únicamente se tuviera en cuenta el día como unidad de tiempo, usando decimales de día para ajustes más finos. De ésta forma, a partir de un día que se consideraría como origen del sistema, a cada día futuro le correspondería un número real. Así de sencillo. Se establecería un algoritmo de conversión del sistema de días julianos al sistema tradicional de nuestro calendario gregoriano y viceversa para los cálculos. Como todas las ideas verdaderamente buenas, esta era muy sencilla y no tenía más que ventajas.

Sólo faltaba definir el origen. Para ello, Scaliger planteó que dicho día de origen fuera a su vez origen de tres sistemas de cómputo importantes:

1.- El ciclo solar
2.- El ciclo lunar
3.- El ciclo de indicción romana.

CICLO SOLAR

El llamado ciclo solar es el período de tiempo más corto en el cual los d´çias de la semana y las fechas del calendario vuelven a coincidir. Como el año no bisiesto tiene 365 días, hace 52 semanas (364 días) más un día. Esto hace que el 1 de enero de cada año caiga en un día de la semana posterior al del año anterior. El decalaje es de 2 días en año bisiesto. Como los años bisiestos son cada 4, tenemos que cada 7x4=28 años se vuelve a repetir exactamente el ciclo entero.

CICLO LUNAR

También llamado ciclo metónico . La división de tiempo que nosotros conocemos como mes proviene del ciclo de las fases lunares. El mes lunar o mes sinódico es el tiempo transcurrido entre dos conjunciones seguidas del sol y de la luna; o lo que es lo mismo: el tiempo transcurrido entre dos lunas nuevas (29 dias, 12 horas, 44 minutos y 2,8 segundos). Intentando, como siempre cuadrar lo irracional, resulta que 19 años solares equivalen casi exactamente a 235 meses lunares, luego cada 19 años, las fases de la luna vuelven a coincidir .

Número áureo de un año es el orden del año dado dentro de este ciclo de 19. Se considera número aúreo 1 a aquel año cuyas fases lunares del mes de enero se inician el 24 de diciembre del año anterior.

El año 1 de la era cristiana, por ejemplo tenía de numero áureo la unidad.

Este sistema fue introducido por el emperador Dionisio el Exiguo en el año 532 (año con número áureo=1)

INDICCION ROMANA

Este ciclo nada tiene que ver conla astronomía, sino con temas fiscales heredados del imperio romano. Cada 15 años se hacía ena evaluación de los bienes de las personas con el fin de determinar los impuestos a satisfacer al estado. Fue introducido por el emperador Constantino en el año 313, siendo este año el número 1 de su correspondiente ciclo.

Así pues, un sistema que conjuntara los tres ciclos debiera tener a su vez un ciclo de 28x19x15=7.980 años.

Ahora solo faltaba encontrar un origen de cómputo, que sólo podía ser aquel año que tuviera la unidad como valor de los tres ciclos.

Cómo encontrarlo?

Pues muy fácil. Con el auxilio del álgebra, el teorema chino del resto y las congruencias.

Seguiremos explorando el calendario, más que nada para intentar evadirnos de la miseria humana.

El calendario (2)

Pocos temas son más importantes para una civilización agrícola que el momento oportuno para plantar las patatas, los nabos, el maíz o los puerros, y recogerlos. Ni las grandes conjunciones cósmicas, ni el poder astrológico de los planetas, ni las fuerzas ctonico-primordiales (sean éstas lo que sean, si es que son algo, que lo dudo...) ni los dioses ni los extraterrestres: las patatas y los nabos .

Al no tener en cuenta esa verdad primordial, resulta enigmático el esfuerzo enorme que muchas civilizaciones realizaron para medir el tiempo. La dificultad del asunto está en que los ciclos naturales van a su aire, y los más evidentes (alternancia día-noche) no son los más indicados para medir lo que realmente importa.

Los ciclos naturales más evidentes , además del día son las fases lunares, las estaciones y el año. Quitemos las estaciones. No por no importantes; precisamente ésas son las importantes, las quitamos porque van incardinadas en el año, siendo por lo tanto éste el que hay que medir.

No vamos a extendernos mucho en los tópicos más corrientes del tema: los solsticios, los equinoccios, las estaciones, y todo eso. Daremos un brevísimo resumen para entender lo posterior, porque está sobradamente tratado en mil lugares de la web. San Google irá raudo a la ayuda de quien lo invoque correctamente.

Por tanto, daremos unas someras pinceladas mínimas para entender la visión de conjunto, sabiendo que nos metemos en terrenos que no dominamos: la astronomía, y pidiendo perdón por las erratas que podamos cometer. En todo caso, la incursión será breve, y en el siguiente post volveremos a la matemática de las congruencias y al cómputo por días julianos.

El año no puede ser definido por los creadores de los calendarios como el período de tiempo que tarda la tierra en dar la vuelta al sol por motivos epistemológicos evidentísimos: no se sabía que tal cosa ocurriera. Lo que sí se sabía es que a latitudes medias, el curso del sol sobre el cielo variaba un poquito de día en día, y se repetía cada 365 días, más o menos. El camino que recorre el sol en el cielo a lo largo del día está inclinado respecto al horizonte, con una pendiente que depende de la latitud del punto de observación. En los polos hace círculos palalelos al horizonte sin ponerse en todo el día (latitud 90º) en el ecuador sale y se pone perpendicular al suelo (latitud 0º), y por eso los amaneceres y anocheceres son muy bruscos. En las latitudes medias, el arco solar tiene lógicamente inclinaciones medias.



El punto de salida (orto) o puesta (ocaso) del sol, va oscilando a lo largo de los días del año, marcando cuatro momentos no demasiado difíciles de concretar con alguna exactitud: los dos extremos, en los que el sol sale y se mete más al norte o más al sur; y los dos medios. Hoy los conocemos como solsticios y equinoccios. Equinoccio proviene de la palabra euqus : igual y nox : noche, cada año suceden dos acontecimientos de este tipo el de primavera y el de otoño, con fechas aproximadas del 21 de marzo y el 20 de septiembre, respectivamente. En ambos, el día y la noche tienen igual duración.
Cuando el sol sale más al norte, el recorrido en el cielo era más largo, consecuentemente hace más calor y las noches son más cortas: estamos en verano. Cuando el sol sale más al sur, ocurre exactamente lo contrario. Soy plenamente consciente de mi asqueroso eurocentrismo: en el hemisferio sur las cosas ocurren exactamente igual, pero al revés

Pues bien; sirva todo esto para tener una idea clara: todo agricultor sabe que es peligrosísimo sembrar antes de un determinado momento, por mil motivos: una helada tardía puede acabar con la cosecha, por ejemplo. Sembrar demasiado tarde trae consecuencias igualmente desastrosas; y la recolección debe ser realizada también en momentos determinados. No debemos olvidar que la consecuencia de un error grave en este “detallito” es el hambre y la muerte.

Para la época de los romanos, el tema estaba aparentemente solucionado: el Calendario juliano contemplaba 365 días , y cada cuatro años había un día adicional. El calendario tenía 12 meses, comenzaba en marzo (como debe ser, no como nosotros), y terminaba en febrero. Por eso es Febrero el mes irregular que carga con el día adicional cuando el año es bisiesto.

¿Qué se había conseguido con ello? Se había conseguido una duración media del año de 365,25 días. Sin embargo, la naturaleza es terca en su querencia por los irracionales, y la duración del año trópico (intervalo entre dos equinoccios de primavera) es de 365 días, 5 horas, 48 minutos y 46,43 segundos.

Eso significa que el error de 11 minutos y 14 segundos. No parece gran cosa, pero ¡es acumulativo!

Esto quiere decir que cada 128 años se comete un error de un día entero de adelanto del calendario juliao respecto a la naturaleza. Allá por 1.582 el decalaje era de 10 días.

La solución fue la revisión completa del calendario: se suprimieron 10 días (el día siguiente al 4 de Octubre de 1.582 fue 15 de octubre), y se redujo el número de años bisiestos de la siguiente forma: los bisiestos múltiplos de 100 sólo seguirían siendo bisiestos si además son múltiplos de 400. De esta forma, se corregía el error acumulativo hasta cotas muy pequeñas. Lo suficientemente pequeñas como para olvidarse del problema en varios milenios.

La penetración del nuevo calendario fue paulatina, pero terminó por imponerse en el mundo, que es como los occidentales solemos llamar al mundo occidental cuando nos referimos a él, haciendo alarde de una miopía sin par.

A pesar de todo, los astrónomos utilizan otro calendario para ellos solos. Es el calendario de los días julianos , que nada tienen que ver con el calendario juliano. Para ver su origen, significado y utilidad, tendremos que aprender congruencias, y pasearemos por conceptos tan poco habituales en la vida diaria como números aúreos , indicción romana , y maravillas similares...""

El calendario

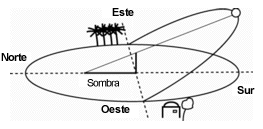
Les propongo un paseo matemático alrededor del calendario.

El tema es algo arduo, de manera que deberemos hacer acopio de provisiones. Para este paseo bastará con llevar ganas de llegar a la meta, y como siempre, la meta será lo de menos. Lo importante será el propio camino.

A lo largo de esta caminata, veremos que la naturaleza gusta de los números irracionales, lo cual es una faena para nosotros los humanos. Sabemos( porque lo sabemos, nooo?) que un número irracional puede expresarse con la precisión que queramos mediando una división de dos enteros, pero sucede que cuanta mayor precisión queramos, más grandes deberán ser numerador y denominador. No obstante, los planetas y los satelites se obstinan en tener períodos de rotación irracionales unas respecto a otras, salvo los notables casos de resonancia .

Esto hace que el tema de la medición del tiempo a largo plazo sea exquisitamente complicado.

Revisaremos los conceptos de congruencias, con las que tanto trabajó el bueno de Euler; echaremos un vistazo al Teorema chino del resto , e intentaremos comprender el sistema actual de calendario, conocido como Calendario gregoriano . Veremos también el sistema astronómico de datación temporal, conocido como el sistema de los días julianos , y veremos la explicación de porqué los astrónomos actuales fechan sus eventos en un extraño calendario en el que los días son la única unidad, arrancando en la estrambótica fecha del 1 de enero del año 4.713 antes de Cristo.

Todo esto lo haremos con la humildad necesaria al comprender que civilizaciones diferentes solucionaron el tema incluso desde antiguo de formas diferentes; algunas muy buenas y alguna extraordinariamente buena.

Y es que en contra de lo que piensan los amantes del misterio barato, los antiguos eran antiguos, pero no gilipollas.

Todo ello en post subsiguientes, si les apetece.

Afinando conceptos sutiles

Este blog no está pensado en un público matemático. Sería como invitar a Edurne Pasaban a dar un paseo por la loma que hay detrás de mi casa. Este blog se hace pensando en amigos de la reflexión, en personas que disfrutan pensando un ratito y apreciando la belleza. Este blog es como una invitación a pensar la matemática sin gran esfuerzo.Por eso, a veces los conceptos que aquí se explican no tienen el rigor preciso que un matemático exigiría.

Sin embargo, y dado que el rigor es precisamente la marca de la casa de todo quehacer matemático, lo que sí podemos es ir afinando detalles para comprender que tras una secuencia de símbolos (una cadena bien formada, que diría alguno), hay ideas precisas, afiladas como bisturíes.

Invito al lector no acostumbrado al lenguaje matemático a que compare la definiciópn del post anterior con la de este. Hay alguna pequeña diferencia. ¿Cuál es el sentido? ¿En qué mejora ésta a aquella? Probablemente, como nos ha pasado a todos, tras un momento de incertidumbre, se hace la luz repentinamente y lo comprendemos todo de un plumazo. Esa es la sensación "Ajá", que decía Martin Gardner.

Pero vaya, es una invitación que pueden aceptar, o no aceptar.