Los grupos cíclicos
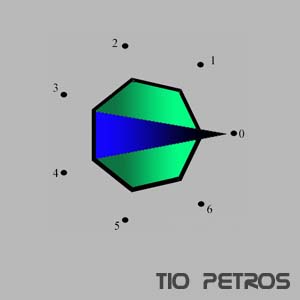
En el post anterior hemos presentado los números complejos de módulo unidad como operadores de giro sobre otros números complejos. Esta forma de verlos nos lleva a pasear por los llamados grupos cíclicos. Espero que sea un paseo agradable.Supongamos que tenemos un selector de n posiciones, como el de la figura. El aparato está siempre en alguna de las n posiciones, y nosotros podemos actuar sobre él, girando la aguja hasta donde nos plazca (siempre hasta una de las n posiciones fijas).
Tenemos por tanto dos conjuntos perfectamente diferenciados, al conjunto de las posibles posiciones del selector, y el conjunto de las posibles acciones nuestras sobre el mismo. Llamaremos X al primero y G al segundo.
Está claro que el conjunto X tiene siete elementos en la figura, y n elementos en el caso general. Los representaremos con números naturales.
X={0,1,2,3,4,5,6}
Los elementos del otro conjunto no son posiciones según hemos dicho, sino nuestras acciones sobre el selector. Podemos girar a la izquierda, o a la derecha hasta la siguiente posición, o podemos girar k posiciones a la izquierda o a la derecha. Consideraremos acciones diferentes las que produzcan resultados diferentes, lógicamente. Esto quiere decir que efectuar un giro de una posición a la derecha es lo mismo que hacerlo de (n-1) posiciones en sentido contrario.
Así pues, el conjunto G también tiene n elementos, que denominaremos así:
G={g0, g1, g2,..., gn-1}
Donde gi será el giro de i posiciones a la izquierda. (exactamente podría ser en sentido contrario, pero sucede que cuando un servidor debe elegir entre derecha e izquierda, pues eso; elige).
El conjunto G podría ser perfectamente el conjunto de las n raíces enésimas de la unidad del post anterior. No en vano adelantábamos allí que dichos números complejos podían entenderse como giros de una amplitud de la enésima parte de una vuelta, o cualquier múltiplo de esta cantidad.
Pues bien, este conjunto G es más que un conjunto. Es un grupo. Ahora explicaremos esto. Pero de momento diremos que este grupo actúa sobre el conjunto de estados X.
Esta actuación implica considerar loe elementos de G como operadores que afectan a los estados (elementos del conjunto X)
Así, g1(0) ( el operador g1 actuando sobre el estado 0) quiere decir el estado que tenemos cuando estando previamente en el cero hacemos un giro de una posición a la izquierda. Evidentemente g1(0)=1. Es fácil ver la veracidad de las siguentes expresiones:
g0(x) = x, para todo x X
g2(0) = 2
g1 (g2(0)) = g1 (2) = 3
La primera igualdad nos dice que el giro nulo deja todo como estaba. La última supone la realización de un giro y luego otro. El resultado siempre se podría haber hecho de una sola vez mediante un giro único.
Efectivamente, existe una operación natural entre los elementos de G: gi* gj, que consiste simplemente en ejecutar ambos seguidos; primero el que escribimos a la derecha (gj) y luego el otro (gi).
Además, dado un giro concreto, siempre hay otro en G que deja las cosas como estaban. Diremos que cada elemento de G tiene un simétrico. Denotaremos g-1 al elemento simétrico de g.
Queda una última propiedad, que permite agrupar giros por parejas sin alterar el orden en el que operan:
gi* (gj *gk) = (gi* gj) *gk)
Todo conjunto con una operación que tenga estas propiedades será llamado desde ahora un grupo .
Este grupo nuestro tiene unas propiedades adicionales que no satisfacen todos los grupos, ni mucho menos. Por ejemplo: uno sólo de sus elementos puede generar a todos los demás por simple composición consigo mismo. Esto quiere decir que a base de la única acción de girar una sola posición podemos generar todas las acciones del grupo. En lenguaje técnico diremos que G es finitamente generado, cuando todos los elementos son generados por composición de un grupo finito de ellos, y monógeno cuando lo son por uno solo de ellos , como en nuestro caso.
G =[ g1]
Diremos que g1 es un generador de G
Noten que hemos sustituido las llaves {} de los conjuntos por corchetes []. En la notación habitual se usan los signos mayor y menor que, pero me dan problemas porque Blogia los interpreta como comienzo de etiquetas HTML...
Llamaremos orden de un grupo G a su número de elementos, y escribiremos o(G)=n. Llamaremos orden de un elemento de G al orden del subgrupo generado por dicho elemento. Está claro que si y solo si dicho elemento gk es un generador de todo G , entonces o(gk)=n.
Llamaremos cíclico a un grupo tal que todos sus elementos son generados por uno solo. Es evidente que nuestro grupo de giros del conmutador es un grupo cíclico.
Basta por hoy. Terminamos con una pregunta tan sólo para aquellos que nada sepan de teoría de grupos:
Nuestro grupo completo es generado por uno sólo de sus elementos, lo hemos visto con el elemento más sencillo g1, que es el menor giro posible a parte del nulo g0, claro. El elemento nulo malamente puede generar nada distinto de sí mismo.
Pero ¿los demás?. ¿Es g2 también un generador de G ?, ¿Y un gk genérico? ¿Depende de algo que la respuesta sea positiva o negativa?
Les espero para continuar hablando de grupos cíclicos.
22 comentarios
MARIA INES -
estoy elaborando un programa para mi tesis y no puedo encontrar un algoritmo adecuado, por favor ayudenme.
martin -
sandra gutierrez -
Sandra Almeida -
Einar Alexander -
Cluje -
Chau.
Sergi -
TioPetros -
Sin embargo, a veces denominan a dicho grupo como grupo cíclico infinito...
En resumen: aquí hablaremos de grupos monógenos como los que tienen un sistema generador unitario, y llamaremos cíclicos tan sólo a los momógenos finitos, como el de los giros del selector del post.
TioPetros -
Adrian -
Three-Dimensional Geometry and Topology
Cluje -
juan -
es muy interesante ver una nueva forma de hacer las cosasque ya habiamos hecho de otra manera.
seguire encantado el curso de este tema. a ver si enras a los cuaterniones, como te dijo alguien no se cuando.
por cierto, y abusando un poco de tu blog: me gustaria dar difusion a una denuncia personal que hago por la red despues de hacerla judicialmente. visitar mi blog para mas señas. si te parece incorrecto, borra este comentario.
muchas gracias.
Vailima -
Un abrazote
Sergi -
Sergi -
Voy encajando con dificultad las piezas. Supongo que el problema es no haber manejado nunca antes el concepto de operador. Cuando leí el post anterior y comentabas que podíamos considerar a esos núemros como operadores no entendí muy bien, pero como no formaba parte del núcleo del post (o eso me parecía) pasé de largo.
Una cosa más, abusando completamente. A primera vista, parece que un grupo cíclico y un grupo monogéneo son la misma cosa (aquel grupo que puede generarse a partir de uno sólo de sus elementos). Supongo que hay algún detalle que se me escapa, ya que si se usan dos términos debe ser por que hay alguna diferencia.
Tio Petros -
Un grupo es un conjunto de operadores cuando interpretamos sus elementos como operadores. En los dos posts anteriores hablábamos de ciertos números complejos que pueden interpretarse como operadores, porque cuando actúan sobre otros números complejos, hacen cosas sobre ellos (giros en el caso que nos ocupaba).
Una cosa es un operador , que en este sentido es un elemento que actúa sobre otro, y otra muy diferente es una operación , que es una aplicación que a cada par de operandos le da el resultado de la operación. "*" es una operación interna definida en un conjunto de operadores, que le da una estructura de grupo.
Lo que ocurre es que las acciones sobre cosas en el aspecto más general, admiten una operación trivial, que es la composición consistente en realizar una acción y luego otra. COn dicha operación , el conjunto de operadores es un grupo.
Sin embargo, podemos perfectamente hablar de un grupo como un simple conjunto de elementos con una operación interna que bla,bla,bla... sin mencionar para nada que esos elementos pudieran ser operadores, que operan sobre un conjunto X ajeno al grupo al que pertenecen, claro está.
No dudes en preguntar si algo no se entiende, Sergi.
Un cordial saludo.
Sergi -
Vaya por delante que no soy matemático, sino un simple aficionado y que lo único que recuerdo sobre grupos es una vaga sensación de que una vez, en la infancia, algú profesor me explicó que los enteros con la operación suma constituían un grupo. por aquello del elemento neutro, opuesto, propiedad asociativa... (perdón si digo algún disparate, es que hace muchos años de eso).
Ahora, por lo que dice Tio Petros en el comentario, entiendo que un grupo es siempre un conjunto de operadores, aunque también me parece que para poder hablar de que ese conjunto es un grupo lo fundamental es el operador "*" que no es uno de sus elementos. Repasando las propiedades que se enumeran en el post, me parece reconocer lo del elemento neutro y demás que antes mencionaba, pero entonces...
¿Es que los enteros son operadores? ¿Cúal sería el conjunto de estados? ¿O es que, aparte del nombre, una cosa no tiene nada que ver con la otra? ¿O es mi memoria la que falla estrepitosamente?
Perdón por el comentario tan largo y por la empanada...
TioPetros -
He dudado si empezar por la acción de un grupo sobre un conjunto para explicar los grupos cíclicos. No parece el orden lógico porque siemrpe hemos estudiado los grupos por sí mismos, y posteriormente las acciones de grupos sobre conjuntos.
El motivo por el que lo he hecho es el siguiente: quería desde el primer momento empezar con un ejemplo (el selector). Es un peligro confundir los estados del selector con laos acciones que hacemos sobre el mismo, porque los estados no forman grupo alguno al no haber ninguna operación de composición de estados; sin embargo las acciones sí. ¿Cómo diferenciar ambas coas desde el primer momento? Pues introduciendo la acción del grupo de giros sobre el conjunto de estados. Así, de paso a un posible lector que vea esto por vez primera se le quedará la idea de que los elementos de un grupo son operadores...
juan -
a mi me explicaron los grupos ciclicos sin recurrir a acciones de grupos en conjuntos, y debo decir que esta nueva forma me parece algo mas dificil de entender. no obstante, lo has explicado de forma muy clara.
esperare con ansia el proximo post. no te chafare la sorpresa del acertijo, que yo ya la se.
samu -
TioPetros -
Tienes razón, el quid de la cuestión está en el orden del grupo, y sus divisores.
Lo vemos enseguida.
Jorge -
De teoría de grupos sé (sabía) menos que lo que acabo de leer, pero como esto es como el paso de las horas en el reloj, puedo afirmar que hay valores de k que no generarán a todo G: Empezando en una hora par, y avanzando de 2 en 2, nunca alcanzaremos una hora impar; tampoco lo lograremos si vamos de 4 en 4, o de 6 en 6.
La clave está en que 2, 4 y 6 son divisores de 12.