Un cuerpo algebraicamente cerrado
Cuando el cuerpo de los números reales estuvo razonablemente bien construido como el conjunto cociente de todas las sucesiones de Cauchy de racionales con la relación de equivalencia apropiada, se consiguió una proeza. Se tenía ya rigurosamente construido un cuerpo arquimediano, ordenado y completo.Sin embargo, en cierto modo el cuerpo R era decepcionante: una simple ecuación de segundo grado tal como ésta:
x 2+1=0
no tenía soluciones en él.
A nadie se le escapará que no estoy presentando las cosas cronológicamente: era de antiguo conocido que no existen soluciones reales de ecuaciones muy sencillas. Sin embargo el paso siguiente, que consistía en la construcción de un cuerpo algebraicamente cerrado en el cual todo polinomio de coeficientes racionales (o enteros, lo mismo da) tenga solución en su seno, estaba al alcance de la mano. De hecho, intelectualmente la construcción de R fue un reto mucho mayor que la construcción de C , el cuerpo de los números complejos, ya que este surge casi trivialmente con la consideración de pares ordenados (a,b) de números reales si definimos bien las operaciones suma y producto.
Tenemos así un cuerpo numérico algebraicamente cerrado, como nos lo enuncia el merecidamente famoso Teorema fundamental del álgebra , que dice que
todo polinomio a coeficientes complejos tiene un raíz compleja, es decir existe un número complejo donde el polinomio evalua a cero.
Esto es lo mismo que decir que todo polinomio de grado n con coeficientes complejos (o naturales, pues los naturales complejos son); tiene en C exactamente n soluciones, no necesariamente diferentes.
Efectivamente, si Pn(x) es el polinomio original, el enunciado del teorema asegura la existencia de una raíz w, con lo que podemos expresar el polinomio como:
Pn(x) =(x-w)·Pn-1(x) .
Ahora aplicando lo mismo al nuevo polinomio con un grado menos Pn-1(x) y sucesivamente hasta llegar al polinomio de grado uno, tenemos n raíces, no necesariamente diferentes de Pn(x) en el seno de C .
Particularmente, la ecuación
x n=1
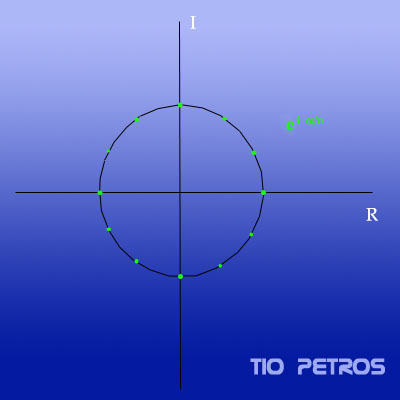
tiene n soluciones en C , ésta vez todas diferentes. Se trata de las denominadas raíces de la unidad .
El estudio de las mismas es una bella y multidisciplinar parcela de la matemática que es: la teoría de variable compleja , la geometría, la teoría de grupos cíclicos y la teoría de polinomios ciclotómicos beben de esta fuente de cristalinas aguas.
De ello nos ocuparemos en los próximos posts.
Me parece una buena manera de iniciar el año. Espero que a ustedes también.
10 comentarios
Sildenafil -
kotah love! -
Patricia -
pedro -
samu -
Manuel -
Saludos, he buscado en la web el email del tio Petros y no lo he encontrado; queria mandar un problema a ver si despierta interés y me ayudan a resolverlo:
Dos matemáticos contemplaban la devastación producida por el huracán Juan al parque nacional Victoria. Hubiera podido ser peor, dijo uno de ellos. Se han perdido menos de un tercio de los árboles que había.
El otro respondió: Sí, de hecho, si multiplicas por 10 el número formado por las dos últimas cifras del número de árboles que había antes y lo sumas al número obtenido de borrar estas dos últimas cifras de este número, obtienes el números de árboles que hay ahora.
Para no ser menos, el primer matemático dijo: Y si tomas el número de árboles que se han perdido, inviertes el orden de sus dos últimas cifras y además insertas un cero justo delante de estas dos cifras, entonces obtienes el número de árboles que había antes más el número de árboles que hay ahora.
¿Cuantos árboles quedan en el parque?
Tomado de la competicón Apics 2003. Lo he mandado también a la lista de matracas.
Gracias.
juan -
por fin, teoria de galois a la vista!!! ecuacuines algebraicas por un tubo, señoras y señores...
tio petro: como siempre, un placer leerte de nuevo. feliz año nuevo, aunque sea el ultimo en decirtelo...
Crystal -
A ver qué nos cuentas, Tío Petros. Feliz año!
TioPetros -
Carlos -