Las raíces de la unidad (2)
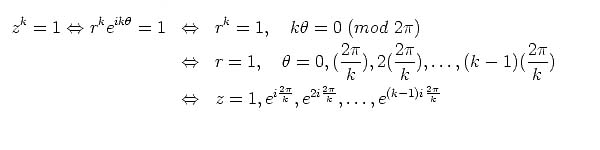Es muy notable que con los pocos conceptos desglosados en el post anterior se esté ya posibilitado para encontrar los k números complejos que satisfacen la ecuación:zk=1.
Más notable aún es la brevedad del desarrollo necesario para hacer tal cosa, tres renglones, como pueden ver en la ilustración que encabeza este post.
Sea z un número complejo raíz k-ésima de la unidad. Intentemos seguir paso a paso los tres renglones de la demostración:
Por su propia definición podemos poner:
zk=1 Ecuación(1)
Pongamos tanto z como el 1 (que es un número complejo al fin y al cabo) en la forma exponencial (que llamaremos a partir de ahora forma polar) que aprendimos en el post anterior. z es un complejo genérico del que a priori nada sabemos, luego su forma será completamente general:
z=r·eix donde la x sustituye a la letra griega zeta, que no puedo reproducir aquí.
1= ei·0
No tenemos más que sustituir ambos números en la ecuación (1) anterior, teniendo en cuenta que zk tiene la forma:
zk=(r·eix)k =
rk·eikx
Por tanto la igualdad (1) se convierte en:
rk·eikx = ei·0
El resto del desarrollo es pura aritmética, igualamos coeficientes y exponentes en ambos miembros y obtenemos el resultado que anunciábamos: las raíces k-ésimas de la unidad son k números complejos sobre la circunferencia unidad, y dividen a ésta en k partes iguales.
Lo vemos mejor en la ilustración siguiente, para k=7:
Cada punto es una rotación del anterior de un k-ésimo de vuelta, o sea, de 2PI/k radianes. Esta reflexión nos da un nuevo punto de vista de estos números complejos: no como números sino como operadores. Me explico.
Se tenemos un complejo en forma polar z=r·eix y lo operamos con eiw multiplicando ambos, obtenemos lo siguiente:
z=r·eix· eiw= z=r·ei(x+w)
Esto es: obtenemos un nuevo punto que es el primitivo, pero girado un ángulo w en sentido contrario a las agujas del reloj. Así, podemos entender un complejo unitario (de módulo igual a uno) como una operación giro alrededor del origen de coordenadas. Esto será importante en el post siguiente, en el que hablaremos de grupos cíclicos.
5 comentarios
Celic -
Crystal -
Por aquí voy, para que te hagas una idea. Espero que me de tiempo a leerme el siguiente post, que de momento va mu bien ;)
samu -
TioPetros -
Por lo demás, mera apariencia.
Ví el símbolo por ahí y me gustó. Nada más.
Lo de los cuaterniones... ya veremos. Seería bastante buen momento para hablar de ellos, verdad?
Jorge -
Cuando termines con los complejos, ¿hablarás de los cuaterniones, o los dejarás para más adelante?