Base matemática de la música (2)
Según veíamos en el post anterior, las escalas musicales occidentales antiguas se construyeron en torno a la idea de producir la máxima consonancia posible; cosa que ocurría cuando la relación de las frecuencias de dos tonos tocados simultáneamente era expresable mediante una fracción lo más simple posible. Dado que un tono base y otro de frecuencia doble dan la sensación del mismo tono pero más agudo, lo natural era considerar esa distancia como la total que había que subdividir; independientemente de que pudiera adjuntarse otra hasta la frecuencia triple, cuádruple, etc...La fracción más simple posible es la de 3/2, que es la que usábamos para crear nuevas frecuencias a partir de la de origen, que llamaremos tónica . Si la tónica es un Do , al multiplicarla por 3/2 obtendremos un Sol . Este intervalo se denomina una quinta justa. (Esta denominación tiene mucho sentido: para llegar del Do al Sol hay que pasar por cinco notas: DO, Re, Mi, Fa, Sol; ambas incluidas. Por supuesto, una vez que tengamos construida la escala!!!)
Pues bien, decíamos que a base de quintas justas íbamos construyendo las demás notas de la escala. Cuando obteníamos valores superiores a 2, nos salíamos de la escala ( la nota obtenida era más alta que el Do superior al que queríamos llegar), con lo que simplemente dividíamos por dos, y volvíamos a caer en nuestro dominio a subdividir. Se trata de una operación módulo una octava.
Dado que el 2 y el 3 son primos entre sí, no podemos tener esperanza alguna de llegar jamás al Do superior exactamente: iríamos obteniendo infinitas notas por este procedimiento, todas entre ambos Do, de modo que debemos cerrar el círculo de quintas en falso. Efectivamente, alguna vez obtendremos un valor lo suficientemente cerca del Do alto como para asimilarlo.
Esto ocurre tras 12 quintas , más sus respectivas correcciones (dividiendo por dos) para no salirse del intervalo. Efectivamente, 12 quintas suponen siete correcciones ( no hay más que ir obteniendo los valores para comprobarlo) 312/219= 531441/524288=1,0136.
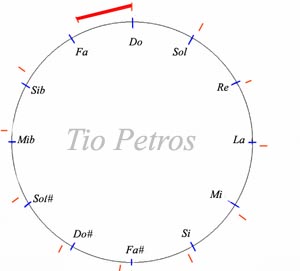
Si vemos la figura, tenemos sobre un círculo de quintas marcados los doce intervalos equidistantes (escala temprada) con segmentos azules, mientras que las notas obtenidas por el método aquí indicado están en rojo. Dado que las 12 quintas son algo mayores que las siete octavas, para cerrar el círculo en falso debemos aceptar el último intervalo (marcado en rojo) bastante más pequeño que los demás. Esta quinta irregular es denominada la quinta del lobo . Cada una de las doce notas obtenidas son las de nuestra escala cromática. El problema que tenemos ahora es ver si podemos distribuir de alguna manera esta diferencia notable de la quinta del lobo entre varias. La solución de repartir equitativamente entre todos los intervalos ( que es lo que hacemos nosotros con nuestra escala actual, o escala temperada) no les gustaba nada a los antiguos, que eran más exigentes y estetas que nosotros, por motivos obvios: nos cargamos todas las quintas justas y ya no existen consonancias perfectas.
Este es un problema sin solución óptima. Hay que optar entre varias soluciones, llamadas temperamentos . Se trata de dividir el déficit de la quinta del lobo entre algunos intervalos, de forma que se mantenga dentro de lo posible la perfecta armonía de 3/2 entre varias quintas.
Para ver cómo lo consiguieron, necesitamos más teoría, que será la semana que viene.
Que tengan mis lectores un buen fin de semana.
10 comentarios
miriam -
rosario -
juan -
es interesantey muy intrigante
karlitas -
federico garcia -
Hay algo que no me cierra y por eso me gustaria encontrar el mapa
Vailima -
un saludo
Crystal -
Rimblow -
Shunt -
Sí, Vailima, ya nos ha cambiado el acorde, ahora está en suspense.
Vailima -
Un saludo