Conceptos

Divergencias modernas.

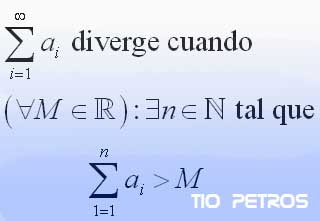Hace unos día vimos cómo Johann Bernoulli demostró que las suma de los inversos de los números naturales era una suma infinita.(En lenguaje de hoy: que la serie armónica es divergente). Dijimos que la demostración hoy no se consideraría rigurosa por el tratamiento del infinito tan alegre que en ella se hace: se considera como un infinito actual, y se opera con él sin ningún respeto.

Hoy vamos a ver, si les parece, cómo se evita este problema y cómo se convierte en rigurosa la demostración.

EL argumento finitista, tan al gusto de la matemática moderna, viene definido en la ilustración. Si uno no está acostumbrado, las frases en las que intervienen los símbolos de para todo , o existe un , son un poco liosas en apariencia, pero un pequeño esfuerzo será recompensado.

Escojamos un número M, tan grande como queramos. Si sucede que sumando elementos de la serie siempre conseguimos sobrepasarlo, entonces decimos que la serie diverge. n es la cantidad de elementos de la serie que hemos tenido que sumar para alcanzar el valor M. Si consigo demostrar que, sin importar el valor de M, siempre habrá un valor de n que cumpla este requisito, habré demostrado que la serie es divergente.

La lógica del razonamiento es aplastante, y así hemos evitado toda referencia al infinito.

En el caso de nuestra serie, la demostración sería así:

Si agrupamos los sumandos de la siguiente manera:

1+[1/2+...+1/10] + [1/11+1/12+...+1/100]+[1/101+...+1/1000]+...

El primer corchete tiene 9 elementos, el segundo 90, el tercero 900 y así sucesivamente.

Para cualquiera de dichos corchetes (por ejemplo el primero) podemos razonar así:

[1/11+1/12+...+1/100] > [1/100+1/100+...+1/100], ya que hemos sustituido todos los sumandos por el último, que es el menor. Y esta última suma vale 0,9 . De la misma forma, cualquier corchete vale 0,9 (90 veces 1/100, ó 900 veces 1/1000, ó 9000 veces 1/10000 da lo mismo, verdad?

Hemos demostrado que podemos agrupar los sumandos de la serie armónica en grupos que sumen más de una cantidad fijada y mayor que cero. Dado que disponemos de tantos grupos de estos como queramos, dado un número M, por grande que sea, nos bastará tomar un cierto números de corchetes de los anteriores para sobrepasar el valor de M.

Por lo tanto, LA SERIE ARMONICA DIVERGE .

Que es lo que queríamos demostrar.

_________________________________________________________________________________


Yo no sé qué les parecerá a ustedes esta demostración, pero aún recuerdo cuando se la expliqué a un buen amigo mío. Se llama Pedro. Le gustó tanto que me impresionó cómo a ciertas personas un buen razonamiento les puede hacer el efecto de una historia bien contada, de una película estupenda o de una música arrebatadora.
Y es que, con ciertas audiencias, da gusto. ;)

NOTA.- La definición "buena" de convergencia de una serie es un poquitín más complicada que la aquí explicada. Ello es debido a que, en la generalidad, una serie puede ser más perversa de lo que es la armónica que aquí nos ocupa. La simplificación ha sido realizada en aras de una mayopr claridad en la definición. En otro post hablaremos de ello.

Magia existencial (o inexistencial !!)

No es mi intención cargar demasiado los post con formulismo matemático por miedo a cansar al personal. Por eso, y dado que los últimos post iban fuertes en este aspecto, vamos a relajarnos un poco.

Hace unos meses comprobábamos una de las propiedades más fascinantes de la matemática: la facultad de postular la existencia de objetos que desconocemos, que nunca hemos visto, pero que podemos deducir sus propiedades una a una antes de encontrarlo. El ejemplo que veíamos era el del poliedro de Szilassi; extraño cuerpo tridimensional cuya existencia demostramos y propiedades en una serie de tres post, antes de mostrarlo en las ilustraciones.



No deja de ser mágico el asunto si lo pensamos bien: demostramos la existencia de un extraordinario poliedro con tan sólo siete caras, con 21 aristas y 14 vértices, que es topológicamente similar a una rosquilla por tener un agujero, y que además cada par de caras se encuentran en una arista. Podemos saber por tanto que todas las caras son hexagonales, pues cada una de las siete debe tener una arista común con las seis restantes. Sabemos también que de cada vértice salen exactamente tres aristas... y sin embargo nada sabemos del aspecto real del mismo... hasta que lo descubre Szilassi y nos lo muestra con exactamente las propiedades que habíamos predicho. El hecho de hacer el post muchos años después del descubrimiento no empaña para nada la belleza del asunto, creo yo...

Pues bien, siendo todo esto extraordinario, puedo asegurarles que hay cosas más extrañas todavía: hay ciertas propiedades que deben cumplir indefectiblemente ciertos objetos matemáticos ¡en el caso de existir!

Nadie sabe si existen o si no existen, pero se sabe que si existieran, deberían cumplir una serie (cada vez más larga) de propiedades. Filosóficamente, uno se podría preguntar de qué leches estamos hablando cuando nos referimos a propiedades de objetos, tal vez inexistentes, verdad?

Estos "objetos" no son geométricos: son números. Concretamente son números perfectos (aquellos cuya suma de divisores propios es igual al propio número, se acuerdan?). Y más concretamente, son números perfectos impares.

Nadie sabe si existen, nadie conoce ninguno. Nadie sabe una razón por la que no deban existir, ni por la que sí deban existir. Sin embargo, se sabe que si existieran, debieran cumplir al menos estas propiedades:

1.- No pueden ser divisibles por 105
2.- Deben tener al menos 8 factores primos diferentes.
3.- Deben ser, incluso el más pequeño, mayor que 10 ³⁰⁰
4.- Su segundo factor primo más pequeño debe ser mayor de 1000
5.- La suma de los inversos de todos ellos, debe ser finita.

La lista de proiedades "descubiertas" para los perfectos impares va creciendo continuamente, y ese crecimiento es el que, precisamente podrá demostrar al final la inexistencia de los mismos. ¿Cómo? Pues muy sencillo. Si algún día se demuestra una propiedad que sea incompatible con alguna de las ya demostradas anteriormente, se habrá demostrado la inexistencia de los números perfectos impares.

Para terminar, permitanme una infantilidad: yo no quiero que eso ocurra . Me parece mucho más interesante que existan que que no existan. Desgraciadamente, si un día decíamos que una de las propiedades del universo es el nulo caso que hace de nuestros deseos, creo que con la matemática pasa igual...lo cual da pie a pensar de un modo platónico en la existencia matemática, y nos llevaría a la eterna pregunta de su los objetos matemáticos se inventan o se descubren, pero eso es harina de otro costal.
___________________________________________________________________________________

Como suele suceder con las demostraciones de los enunciados aparentemente inocentes de la Teoría de números, la complicación y dificultad se hace inusitadamente grande cuando aumenta la fuerza de la afirmación. Para ejemplificarlo, baste ver la demostración de dos afirmaciones más suaves que las que se listan aquí. A saber: todo perfecto impar tiene al menos TRES factores primos diferentes; aquí, y todo perfecto impar tiene al menos CUATRO factores primos diferentes ; aquí.

Tamaños aparentes e ilusiones (2)

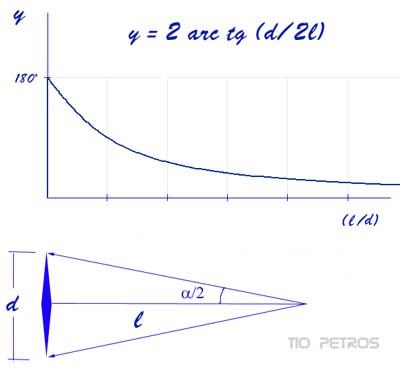Todos sabemos que cuanto más lejos está un objeto, más pequeño lo vemos. Hablamos en todo caso de observación directa, sin instrumentos de aumento. Nos vendrá bien comprender el motivo y cuantificar un poco el asunto. En la figura aparece un objeto, como un rombo alargado, visto desde un punto a una distancia l, siendo d la diagonal mayor del rombo. Lo importante desde nuestro punto de observación es el ángulo alfa que ocupa el objeto. Cuando hablemos del tamaño aparente del rombo, nos referiremos a dicho ángulo. Con un poco de trigonometría, vemos que

tg (a/2)=d/(2·l)

y por lo tanto, a= 2 arc tg (d/(2·l))

Vemos por lo tanto que el tamaño aparente de un objeto depende exclusivamente de la relación (cociente) entre su diámetro real y la distancia que nos separa del mismo. Teneis la gráfica en la ilustración. Conviene recalcar que el eje horizontal no expresa distancias sino cociente de distancias, o si lo quereis: la distancia a la que estamos del objeto observado, tomando el diámetro del mismo como unidad de medida.

Es una función sin sorpresa alguna: decreciente y asintótica a cero, como debía ser. A distancia nula del objeto observado, su visión nos abarca 180 grados, lo que quiere decir que lo tenemos tan cerca que llena todo nuestro campo visual. Es lo que pasa con la tierra, que nos tapa exactamente la mitad del cielo si estamos en una zona completamente llana a ras de suelo.

El sol y la luna están aproximadamente a la misma distancia de nosotros si tomamos como escalas sus respectivos diámetros, de ahí que apreciemos aproximadamente el mismo tamaño en ambos. En ausencia de referencias añadidas, no tenemos evidencia directa de cuál de los dos está más cerca. Parecen dos astros de tamaño similar.

Sin embargo, resulta que el cerebro no se vale únicamente de los tamaños aparentes para estimar tamaños reales, sino que efectúa todo tipo de comparaciones. Pongamos un ejemplo: tengo en una calle a cierta distancia un niño con un globo, y tras él, bastante más lejos, otro niño con otro globo idéntico. Podemos hinchar el segundo globo hasta que desde mi punto de observación tenga el mismo tamaño aparente que el primero, pero en ese caso, no tendré ningún problema para saber que el globo más alejado es más grande: sé que está más lejos porque tengo mil referencias: ambos niños, la propia calle...) y lo aprecio moyor aunque tenga el mismo tamaño aparente que el cercano.

Eso es exactamente lo que pasa con el sol y la luna sobre el horizonte. Nuestro cerebro, por lo visto, imagina la bóveda celeste no como una semiesfera, sino como una cúpula elíptica, de forma que los puntos más alejados están en el horizonte, y el punto más cercano es el cenit. Aunque los tamaños aparentes son los mismos, una luna sobre el horizonte nos parece mayor porque la situamos más lejos que cuando está más alta.

Así de sencillo, sin necesidad de apelar a aberraciones atmosféricas, ni a cosas raras.

Y lo de las montañas que parecen alzarse sobre nosotros cuando nos alejamos en coche?

Si observan la gráfica de la curva de la ilustración, verán que la pendiente de la curva (su derivada, o ritmo de variación) va decreciendo paulatinamente (no podía ser de otra forma, si es asintótica a cero, continua y siempre positiva). Esto quiere decir que las variaciones de tamaño aparente según nos vamos acercando o alejando de los objetos que vemos serán mucho más acusadas para objetos que estén a distancias pequeñas de nosotros en (comparación con sus diámetros, no lo olvidemos !!!). Si nos alejamos de una montaña en coche, nos estamos alejando a una velocidad muy pequeña medida en (altura de montaña)/hora. Sin embargo, todo lo cercano que hace de marco a la montaña (los árboles que vamos dejando atrás, la propia carretera) sufre un efecto muy diferente: nuestra velocidad de separación medida en (altura de árbol)/hora es ahora muy grande a pesar de que nuestra velocidad real es la misma, y por lo tanto todo disminuye de tamaño a ritmo rápido menos la montaña, que lo hace muy lentamente. El efecto conjugado es que la montaña crece respecto al marco de referencia.

Tamaños aparentes e ilusiones

Hace cosa de un mes, me desperté en el momento en que el sol estaba saliendo por mi horizonte. Como no es cosa habitual (que me levante en ese momento, no que el sol salga), le hice una foto con mi cámara digital y me olvidé del asunto. Pasados los días, al ver las fotos me acordé de una desilusión que ya se me había producido en otras ocasiones: el sol (o la luna) sobre el horizonte en las fotos parece ser mucho menor que en nuestro recuerdo. Si no hay efecto de zoom o ampliación posterior, las fotos de puestas o salidas de astros son decepcionantes.

Aunque recordamos la puesta de sol que hemos fotografiado más o menos así:



lo que obtenemos en la foto es algo como esto:



con un tamaño aparente del astro mucho menor que lo que recordábamos.

Dado que nosotros percibimos que cerca del horizonte el sol o la luna parecen más grandes, y dado que la cámara fotográfica no registra dicho aumento aparente de tamaño, la explicación de lo que percibimos deberá ser algo más elaborada que un efecto de aumento por parte de la atmósfera, por ejemplo: si así fuera, la cámara registraría el aumento aparente.

En el próximo post explicaremos los motivos de tal efecto, que tienen que ver con los tamaños aparentes de las cosas por un lado, y con nuestra forma de procesar la información en el cerebro por otra. Además, al explicarlo, podremos comprender las bases trigonométricas de otra ilusión muy corriente: si van ustedes atravesando un paisaje montañoso en coche, dejando las montañas atrás, y se dan la vuelta (NO LO INTENTE SI ES USTED EL CONDUCTOR!!!) para ver por la ventana trasera las montañas de las que se aleja el vehículo, se tiene la poderosa sensación de que las montañas están aumentando de tamaño; alzándose sobre nosotros incluso. En determinadas circunstancias ( si la velocidad del vehículo es grande) el efecto es muy llamativo. La culpa la tiene en gran parte una función arco tangente.

Pero lo veremos en el próximo post, si les apetece...

Definición de geometría

Una de las cosas más extrañas de la matemática es que muchas veces es difícil saber qué estudia una cualquiera de sus ramas. Un buen ejemplo de esto lo tenemos con la geometría . La inequívoca etimología de la palabra nos evoca mediciones de terrenos. Por lo tanto, la geometría sería la parte de la matemática que estudia las figuras, las porciones del plano y sus propiedades.

Rápidamente podemos hacer una extensión del concepto, y englobaríamos dentro de los estudios geométricos las figuras que no son planas: superficies alabeadas, cuerpos sólidos, etc.

En una generalidad creciente, si somos capaces de estudiar espacios de más dimensiones, sus porciones quedarían también dentro del estudio de la geometría. La idea original, como pueden ver, se va desdibujando.

En un ambiente de creciente abstracción como la que ocurrió a mediados y finales del siglo XIX, empezaremos a vez la geometría como el estudio de los subconjuntos de un conjunto general, llegando con Félix Klein a decir que la geometría es el estudio de las propiedades que permanecen invariantes por transformaciones. Cuando más generales son estas transformaciones, más primigenias son las propiedades estudiadas. Tenemos así un conjunto anidado de geometrías diferentes, siendo la topología la más general de todas ellas, por estudiar las propiedades invariantes por homeomorfismos, feo palabro que indica simplemente transformaciones generales continuas (sin romper ni rasgar).

Con los trabajos de Klein se desdibuja la separación entre álgebra y geometría, y empiezan a ser posibles gruesos libros de texto sobre geometría sin dibujo alguno. La tendencia de abstracción crece enormemente con la irrupción del mítico (nunca mejor dicho) matemático Nicolás Bourbaki , llegando a Alexander Grothendieck , con su geometría algebráica a niveles nunca antes alcanzados.

¿Qué es hoy la geometría?

El 5 y 7 de febrero de 1.934, el matemático holandés Van Schouten dió dos conferencias con cuyo título era precisamente ésta pregunta. Según cuenta Raymond Queneau, Van Schouten repasó las diferentes definiciones que desde Klein se han dado de geometría. Después de haber demostrado que ninguna de ellas resultaba completamente satisfactoria, decidió adoptar la de O. Veblen:

Se llama Geometría a una rama de las matemáticas que un número suficiente de gentes competentes están de acuerdo en denominar así por razones de sentimiento y de tradición.

Que tengan ustedes un feliz fin de semana.

El discreto encanto del conjunto N

La teoría de números es sin duda alguna uno de los apartados más enigmáticos y que mayor fascinación han despertado desde siempre. Se trata de algo tan fácil de definir como el estudio de un único conjunto: el discreto (nunca mejor dicho) conjunto N . Sabemos positivamente que jamás el ser humano será capaz de responder todas las preguntas que dicho humilde conjunto nos plantea; y lo sabemos porque es muy fácil comprender que el número de preguntas diferentes que tiene capacidad de plantearnos es sencillamente infinito.

Además, bajo la apariencia de preguntas sencillas, de conjeturas infantiles, se esconden retos inmensos contra los que se han estrellado las mentes más poderosas del planeta. No en vano Erdös decía que si se plantea un problema en términos sencillos y no obtiene respuesta satisfactoria en un par de siglos, estamos ante un problema de teoría de números.

La Conjetura de Goldbach pertenece a esta especie. Otras conjeturas son muy famosas, e incluso muy importantes, como la conjetura de Riemann o la conjetura de Poincaré ; sin embargo, para explicar estas últimas hace falta que el interlocutor tenga unos ciertos conocimientos, o al menos hace falta hacer una buen introducción. La de Goldbach en cambio es meridianamente clara para cualquier persona, independientemente de su formación matemática: todo número par es la suma de dos primos.

Es la inconcebible dificultad de la demostración de esta frase lo que atrae a los matemáticos. El origen de esta conjetura parece datarse en 1742, cuando un oscuro matemático de nombre Christian Goldbach le escribe una carta al gran Leonard Euler y le comenta, marginalmente, que, hasta donde ha podido comprobar, todo número par puede escribirse como la suma de dos números primos.

Otra de las fascinaciones del conjunto N es la distribución de los números primos. Me van a permitir que les hable hoy de una fascinación escondida del conjunto N , relacionada con esta distribución.

Todo el mundo sabe que los primos son aquellos números que sólo se pueden dividir exactamente por sí mismos y por la unidad, revelándose así como los ladrillos a partir de los que se construyen los demás. Su aparición en el seno de N es errática: existen porciones de N tan grandes como queramos dentro de las cuales no hay ningún primo. (¿Lo sabía el lector? además, esto último es extraordinariamente fácil de demostrar). Sin embargo, parecen existir una infinidad de primos gemelos, que sólo distan dos unidades de uno a otro.

Sin embargo, aunque la distribución en sí es impredecible, el acumulado de la misma, esto es: el número de primos existentes desde 1 hasta n, sí que tiene una cierta distribución “conveniente”. Se trata del famoso teorema de los números primos , que afirma que dicho número tiende asintóticamente al valor del logaritmo integral. No nos importa ahora qué es este logaritmo integral. Es simplemente una función concreta.


Donde dicho logaritmo integral toma la forma siguiente:


Pues bien: aunque el comportamiento asintótico (para n tendiendo a infinito) parece estar claro a partir de este teorema, lo que no está nada claro es si para cada n concreto el número de primos menor que n se acerca al logaritmo integral por arriba o por abajo. Basándose en extenuantes comprobaciones, se averiguó que el número de primos era siempre menor que el correspondiente logaritmo integral : se acercaba por abajo.

El propio Gauss, que no era amante de conjeturas, conjeturó que esto era así para todo n. Pues bien, Skewes demostró (ojo, he dicho demostró, no conjeturó) que la desigualdad se invierte para un número muy grande.

Esto es muy curioso. Para empezar, la demostración utiliza la conjetura de Riemann . Una demostración que utilice una conjetura, no es una demostración, sino otra conjetura, me dirán ustedes. Y sin embargo no es así: se asume que la conjetura de Riemann es cierta, y se demuestra que existe un número a partir del cual la desigualdad anterior se invierte. Luego se asume que la conjetura es falsa, y también se demuestra que existe otro número a partir del cual la desigualdad se invierte. Ambos números son cotas que pueden ser reducidas en trabajos posteriores más finos; pero en todo caso son demostraciones de que al menos a partir de dichos números, la desigualdad se invierte (siguiendo cumpliéndose el teorema de los números primos, por supuesto).De esta forma, hemos independizado nuestra afirmación de la conjetura en la cual nos apoyábamos para hacer nuestra demostración (nos apoyábamos en sentido positivo, o negativo).

Lo que añade mucho encanto al asunto es la extraordinaria, devastadora, inmensa magnitud de las cotas obtenidas, llamadas primer y segundo números de Skewes.

Sus valores son:





Apenas existen trabajos matemáticos que involucren a números enteros más grandes ⁽¹⁾ .No son grandes: son absurdamente grandes. No hay con qué compararlos, sobrepasan todo entendimiento. El número de electrones de trillones de universos como el nuestro es prácticamente cero en comparación. Ni los indios en su obsesión habían imaginado jamás nada parecido.

Y todo esto dentro del humilde conjunto N , el que surgía del vacío como una joya zen... increíble.


Nota (1): De hecho, sí existen números mayores en la historia de la matemática, el número de Graham por ejemplo. Son tan grandes que incluso la notación exponencial se muestra impotente para expresarlos, y ha habido que inventar otra notación específica para ellos.

Conjeturas, conjeturas...

Ya lo hemos dicho alguna vez: la matemática no es el arte de hacer conjeturas. Es el arte de hacer demostraciones. Y de hacerlas bien. Cantidad de conjeturas se han demostrado falsas a lo largo de los siglos, es tan fácil hacer una conjetura...

Un ejemplo es la Conjetura de Polyà:

Afirma que Existe igual cantidad de enteros con número par de factores primos que enteros con número impar de factores primos

Un vez realizada, ahí queda para la posteridad; pero tiene algún interés? Permítanme que lo dude. El interés de la matemática no reside en la dificultad de demostrar la primera barbaridad que se le ocurra a un matemático.

Además, esta conjetura se demostró falsa (C.B. Haselgrove: A disproof of a conjecture of Polyà, Mathematika, tome V,1958), con lo cual no quedó nada interesante del asunto. Si al menos la demostración hubiera sido "elegante", pero no, se trató de una comprobación por ordenador de que la conjetura fallaba más allá de la cota 1.845 · 10³⁶¹.

Una conjetura no vale nada... a no ser que pasen varios cientos de años, y nadie pueda demostrarla, ni en sentido afirmativo ni en sentido negativo. Y aún así, es la demostración la que tendrá interés, no el mero enunciado de la conjetura. Es la demostración, y la consiguiente elevación a rango de Teorema la hazaña digna de merecer una edición especial de sellos de correos (ver imagen).

Piensen ustedes: ¿qué importancia puede tener la mera afirmación de la existencia o inexistencia de un número entero n tal que la ecuación xⁿ+yⁿ=zⁿ no tenga solución para ninguna tripleta (x,y,z) de enteros? (Ultimo Teorema de Fermat)

Ninguna en absoluto. Esta afirmación se conoció durante siglos con el nombre de El Ultimo Teorema de Fermat .

Aunque debiera haber sido conocido con el nombre de La conjetura de Fermat , porque digo yo que la simple afirmación del autor de que había encontrado una maravillosa demostración del teorema, pero que no le cabía en el margen del libro que estaba leyendo en ese momento ( Aritmética, de Diofanto , creo recordar) no basta para dar categoría a la afirmación de la conjetura. Y ya saben, sin demostración no hay teorema, ni debe haber gloria alguna para el autor.

Lo que sí tiene interés matemático, y mucho, es la respuesta a cualquiera de estas preguntas:

1.- Cómo se demuestra esta afirmación?
2.- Porqué es tan difícil la resolución de este problema?
3.- Qué nuevas matemáticas hacen falta para demostrarla?
4.- Porqué la afirmación es cierta (si lo es), y porqué es falsa en caso de serlo?
4.- Qué nuevas perspectivas nos abre la demostración completa de la conjetura?

Al final, pasa un puñado de siglos, y alguien (Andrew Wiles en nuestro caso), lo consigue.

Lo que no me gusta que se diga es que Andrew Wiles consiguió demostrar el teorema de Fermat.

Andrew Willes consiguió demostrar el TEOREMA DE WILES , cuyo enunciado es:

La conjetura de Fermat es una afirmación cierta ⁽¹⁾

Que no es lo mismo.

(1)NOTA.

Bueno,no quiero engañar a nadie; el enunciado real de Wiles es: Todas las funciones elípticas son modulares , pero palabrita de blogero que ambas afirmaciones deben ser equivalentes...

Los jodidos porcentajes

En dos ocasiones hemos comentado que los seres humanos estamos muy mal dotados en general por la evolución para ciertas actividades que, paradójicamente, son muy importantes para la supervivencia: concretamente para el cálculo de probabilidades.

Acabo de encontrarme con otro tema de importancia enorme en la vida diaria para la cual estamos horrorosamente dotados: la estimación de porcentajes.

He realizado un experimento entre las personas de mi entorno inmediato. Se trata de responder la siguiente pregunta:

Por motivos contables que no vienen al caso, un empresario le explica a un asalariado suyo que va a proceder a subirle el sueldo un tanto por ciento, para decrementarle el mismo porcentaje del nuevo sueldo al día siguiente. Sin embargo, le explica que si lo prefiere lo pueden hacer al revés:comienza por decrementarle el citado porcentaje para luego subirle el mismo porcentaje del nuevo sueldo. ¿Qué debe elegir el asalariado?

Me concederán que el tema está muy cercano a los intereses más cotidianos de cualquiera, y que no es en absoluto complicado; y sin embargo... pregunten, pregunten.

La importancia de los modelos.

En el post ¿Qué es una teoría? un lector (Ctugha), cuya estupenda bitácora podeis ver aquí me plantea la importancia de los modelos en las teorías: "me parece importante incluir el concepto de modelo para formar el triunvirato de: teorias - modelos - hechos". Efectivamente, así es, y tenía pensado hablar de ello para contraponer la tarea científica genuina con las actividades paracientíficas, que son una corrupción de la idea original. Lo que sigue es un artículo mío que Marcos Taracido tuvo a bien publicar hace muy poco en su excelente página.

LAS PARACIENCIAS COMO PERVERSION METODOLOGICA

Hay veces que uno se encuentra con un artículo, una explicación o un documento paranormal, y capta al vuelo lo falaz de su contenido. Puede ser que el tema tratado no pertenezca a nuestra esfera de conocimiento, pero "sabemos" que nos están contando un cuento. Evidentemente, si el artículo está publicado en Año Cero o Más Allá, la cuestión no tiene mucho mérito, pero muchas veces lo encontramos en nuestro diario, o incluso en una revista de divulgación científica. Las paraciencias son ubicuas, como bien sabemos.
A la gente de la calle le resulta a veces muy difícil detectar la falta de rigor científico en ciertas aseveraciones, y ciertamente la culpa no es suya. Es una de las asignaturas pendientes de los medios de divulgación, asignatura que suspenden repetidamente, dado el nivel de irracionalidad imperante en nuestra sociedad.
¿Porqué es esto así? ¿Porqué es tan difícil defender la razón y tan fácil propagar la superstición? Básicamente la respuesta la sabemos todos: quienes hablan de ciencia y racionalidad no suelen hacer trampas y los otros sí. Ha sido perfectamente explicado en muchas ocasiones, y no es cuestión de insistir en este aspecto.
En lo que sigue intentaré describir es otra de las características paranormales, a nivel algo más escondido: la metodología corrupta que utiliza. Corrupta por tomar el método científico y volverlo del revés para su propio beneficio.
Explicar cuestiones científicas al público en general no es sencillo. Además, la ciencia es difícil, y la paraciencia fácil. Pero explicar cómo funciona la ciencia es bastante más sencillo que explicar ciencia pura y dura, y éste es un conocimiento muy provechoso de poseer. Explicar qué marcas, qué estructura profunda subsiste en el fondo de los argumentos paranormales en contraposición a los que existen en el genuino quehacer científico nos puede servir para ayudar a otros a detectar a tiempo las falacias y las mentiras de la sinrazón paranormal.
No existe un "método paracientífico" para contraponer al científico, pero existen unas pautas que se repiten en los documentos paranormales una y otra vez, cuestiones de estilo aparte.
En un primer e ingenuo vistazo, tanto la ciencia como la paraciencia intentan explicar la realidad. La realidad externa es suficientemente compleja como para dejarnos anonadados. Somos testigos de multitud de fenómenos y procesos que ocurren a nuestro alrededor, cuya explicación se nos escapa; pero dentro de la naturaleza humana hay un impulso que conduce a encontrar una explicación satisfactoria de los mismos.



En una hipotética situación inicial (Fig.1) tenemos al ser humano preguntándose por la explicación de lo que ve, y sin herramientas para llevar a buen puerto tal empresa. Es evidente que tal situación derivó rápidamente a otra bastante más satisfactoria. En ausencia de mejores herramientas, el hombre imaginó que tras el plano real existía un mundo oculto, ordenador de la existencia. El observador no ve ese mundo, sino los efectos que produce sobre el mundo de la realidad. Los llamaremos el plano de lo real y el plano de lo oculto, el plano de los dioses o de las fuerzas sobrenaturales que ordena, crea y destruye la realidad. Ha nacido la mitología, con toda su fuerza explicativa. A nadie se le escapa que esta etapa no ha sido en absoluto abandonada, y que goza de excelente salud hoy en día, incluso en nuestro país. Sin embargo es muy fácil reconocer este esquema, que a nadie engaña.


Las explicaciones que siguen este patrón hablan de dioses, de designios inescrutables, de leyes ordenadoras de la existencia que parten del plano de lo divino, ordenador de la realidad. Mediante su acción, (Fig.2) las fuerzas ocultas intervienen en nuestra realidad. La naturaleza de dicha acción divina (flecha d en la figura) se explica mediante observaciones de la realidad; a menudo muy agudas, pero contaminadas culturalmente por dogmas socialmente consolidados respecto a la naturaleza del plano divino. Esta es la situación hasta los comienzos del pensamiento racionalista, que podemos situar en Asia menor y en la costa jónica con los primeros filósofos griegos. Conscientes de los graves perjuicios que a la búsqueda de la verdad acarreaba el esquema anterior, las mejores mentes del planeta fueron consolidando lo que hoy conocemos como el método científico (fig. 3). La metodología científica no contempla nada más allá del plano real, pero consciente de su complejidad, crea un plano más cercano a las posibilidades de análisis del observador; el plano de los modelos.



Existe una proyección desde la realidad R hasta el modelo M. Como toda proyección, es una simplificación que pretende captar lo esencial de la parcela de realidad que se quiere estudiar.
El quid de la cuestión está en el hecho de que los humanos podemos aprehender y estudiar el modelo perfectamente con el auxilio de la matemática, que se revela así como la herramienta básica para el estudio de los modelos, y por tanto para la investigación científica en general. Al establecer la proyección , queremos que el modelo se parezca a la realidad lo suficiente como para que las conclusiones que saquemos del comportamiento del modelo sean extrapolables al plano real, que es nuestro verdadero interés; y a la vez pretendemos que el modelo sea lo suficientemente sencillo como para ser abordable analíticamente. Este paso maravilloso es posible gracias a nuestra capacidad de experimentar y observar la realidad. La acción o del observador sobre el plano real es el que validará o invalidará el modelo. La existencia de esta realimentación es lo característico del método científico. Los modelos nacen con vocación de explicar los hechos observados, entran en crisis y son sustituidos por otros mejores cuando sea posible. Según este esquema, una teoría científica es una creación humana de un modelo para explicar una parcela de realidad, y no es verdadera ni falsa: es útil o no lo es. El plano real es en última instancia quien valida y invalida los modelos, que sólo existen porque la realidad externa nos queda demasiado grande y lejana. El magnífico éxito de este esquema ha proporcionado un prestigio enorme al método científico, dados los progresos en la comprensión del universo obtenidos. El presente artículo trata de mostrar que las paraciencias son una perversión del esquema anterior.



Es más, defenderé que el esquema de la figura 4 define el concepto de paraciencia, a la vez que explica la metodología corrupta que utiliza, robada del quehacer científico para adueñarse de su prestigio ante públicos poco avisados. Al igual que el método científico, tiene un plano de trabajo más cercano al observador que la propia realidad, pero en este caso dicho plano es el objetivo. Nos se trata de estudiar la realidad, sino de forzar a la misma a adecuarse a dicho plano, que llamaremos plano de las explicaciones a priori . Toda paraciencia trata de preservar sus hipótesis apriorísticas, que son hipótesis no falsables, y por lo tanto no científicas. Para ello, en lugar de existir una proyección de la realidad hacia el modelo, como en el caso científico, existe una retroproyección en dirección contraria, desde las supuestas verdades que queremos preservar hacia la realidad. Así pues, existe una visión deformada de la realidad, coherente con la asunción de los postulados arbitrarios que hay que preservar a toda costa. Este esquema es doblemente perverso, pues además de funcionar al revés, es capaz de usar el lenguaje de la ciencia en su desarrollo. Esto es así porque permite observaciones de la realidad, como en el caso científico, pero sólo si mantienen incólume el conjunto de presuposiciones . Dichas observaciones de lo real pasan por un filtro, de forma que sólo las observaciones que validan las explicaciones a priori son tenidas en cuenta.
De esta manera, la crítica desaparece y el "modelo" se perpetúa, pero la paraciencia se viste de lenguaje científico, pudiendo emplear tendenciosamente cuantas herramientas provengan de la ciencia para revalidar su hipótesis inicial. En el caso del llamado creacionismo científico se ven perfectamente las componentes del esquema. La información a preservar a costa de lo que sea es la creación del hombre por Dios. Este es el punto de partida y de llegada. Todo el registro fósil se ve en consecuencia, y se interpreta de forma que sea consistente con el punto inicial. Las observaciones son filtradas, de forma que siempre favorezcan la hipótesis, pero existen observaciones, lenguaje robado del mundo de la biología y la paleontología, y un aspecto exterior cientifista.
La naturaleza del filtro paranormal no es unívoca, sino cambiante y múltiple. A veces se trata de burdas maniobras de engaño, otras veces la práctica con este tipo de actuaciones hace que el autor del trabajo sea inconsciente de su existencia y no sea un engañador consciente. En muchas ocasiones basta un tratamiento estadístico no correcto de la información recopilada, o incluso una recolección sesgada de la misma. Es perfectamente posible aparentar el rigor, la nomenclatura y las formas del quehacer científico, pero la existencia de este esquema perverso con el plano de las explicaciones a priori a preservar a toda costa, y de la retroproyección del mismo hacia la realidad constituye la "marca de la casa" de los amigos de la paranormal.
Comprender cómo actúa la paraciencia es requisito sine qua non para batallar contra ella, y lo que es más importante: para explicar al oyente menos avisado por dónde vienen los tiros.

Leyes de los grandes números

Ya hemos tenido ocasión de comentar que el concepto de independencia es el que da sabor especial a la teoría de la probabilidad, y lo separa de la teoría de la medida, de la que surge naturalmente.

La definición de independencia de dos sucesos aleatorios es muy simple: Los sucesos A y B son independientes si se cumple que la probabilidad de que se den ambos es igual al producto de las probabilidades de cada uno de ellos. Por ejemplo: la probabilidad de sacar un seis al lanzar un dado es 1/6, y la probabilidad de sacar cara con una moneda es ½. Si lanzamos primero uno y luego otro, o ambos a la vez, la probabilidad de sacar un seis en el dado y cara en la moneda es ½ x 1/6=1/12.

Cuando esto ocure, la materialización de uno de los sucesos nada nos dice de la del otro: un seis en el dado no nos aporta información de lo sacado en la moneda, ni viceversa. Esta última visión del asunto la podemos expresar en forma de probabilidades condicionadas:

P(A/B)=P(A)
P(B/A)=P(B). Si A y B son independientes.


Esto es: la probabilidad de un suceso condicionada al resultado de otro suceso independiente suyo es igual a la probabilidad de suceso sin condicionar. Esta visión es la que nos da la explicación de la palabra independencia utilizada para expresar esta propiedad.

Gran parte del pensamiento mágico e irracional que comprobamos a nuestro alrededor consiste precisamente en negar la independencia a sucesos aleatorios independientes. Por supuesto, a priori no es siempre evidente cuándo unos sucesos son independientes de otros, pero existe una especie de creencia humana en la justicia de los sucesos aleatorios que desvirtúa las apreciaciones de independencia. Según esta creencia no siempre verbalizada ni expresada, parecería que las probabilidades de los sucesivos eventos tienen que irse modificando. Al fin y al cabo, todos sabemos que si tiramos infinitas veces un dado, la sexta parte serán unos, otra sexta parte serán doses, y así hasta los seises. Si por un azar extraño hamos obtenido una racha inusitada de unos, por decir un número, algo tendrá que pasar para compensar este hecho ...

Hace años, traté infructuosamente de convencer durante meses a un compañero de trabajo, entrado en años él y gran aficionado a los juegos de azar, de que aunque el gordo de la lotería llevara muchos años sin acabar en cuatro, por ejemplo, eso no modificaba para nada la probabilidad de que acabara en cuatro el próximo sorteo. Mi compañero no sabía lo que eran las variables aleatorias independientes, pero intuía la existencia de la Ley de los grandes números .

Decimos que una sucesión de variables aleatorias X _n, definidas sobre un mismo espacio de probabilidad obedece a la ley de los grandes números cuando la media de las observaciones de n resultados tiende a la media de las esperanzas de las variables aleatorias de la sucesión según n aumenta.

He puesto la palabra tiende en cursiva para resaltar la informalidad y ambigüedad de la expresión. En efecto, según qué entendamos por tiende , tendremos las llamadas leyes fuertes o débiles de los grandes números. Pero no quiero incidir en ello, lo importante es que tras esta definición existe un montón de teoremas que nos especifican qué propiedades debe cumplir una sucesión de variables aleatorias para que cumpla esta ley de los grandes números. Estos nos irán dando detalles de cómo deben ser estas variables aleatorias para que obedezcan a una ley (fuerte o débil) de los grandes números, llegando a la conclusión de que la mayor parte de los casos que se nos presentan en la vida cotidiana obedecen dicha ley, cuando las variables son independientes. No hace falta una extraña “interconexión” entre las variables para que la media de las mismas se vaya acercando a la esperada.

Varios de estos teoremas son:

Teorema de Tchebychev



Basta que las variables aleatorias independientes tengan la varianza acotada para que cumplan la ley débil (convergencia en probabilidad).

Teorema de Khintchine



Si las variables aleatorias independientes están idénticamente distribuidas, basta que tengan esperanza no infinita.

Es la enorme generalidad de estos teoremas la que nos dice que no es necesaria conexión ni memoria alguna entre los sucesos pasados y futuros independientes para que las aguas vuelvan a su cauce , y la media de las observaciones se acerque asintóticamente al valor esperado. Y nos lo dicen en el estilo habitual en el que nos hablan los teoremas matemáticos: con la certeza de una verdad inmutable, de un hecho incuestionable por toda la eternidad.

Pero claro, mi compañero no creía que un teorema pudiera ser más importante que su fuerte intuición.

Por cierto; nunca ganó un duro con los juegos de azar.

La función de utilidad (2)

Ante un juego, o ante un problema de decisión, tenemos un conjunto de posibilidades de actuación, cada una de las cuales nos da un resultado. Quizás el resultado es determinista, quizás no lo es. En el primer caso diremos que estamos en ambiente de certidumbre, y en el segundo diremos que estamos en ambiente de riesgo.

La manera de unificar ambos ambientes es la siguiente:
Tenemos un conjunto A={A₁, A₂,..., A_n} de posibles estrategias o actuaciones que desembocan en resultados. Se supone que existe una relación entre los posibles resultados, que llamaremos relación de preferencia-indiferencia. El jugador debe saber decidir si entre dos resultados A y B prefiere uno, otro ,o le son indiferentes.

Una función de utilidad es una aplicación definida en el conjunto de posibles resultados A, con valores reales, tal que respeta la relación de preferencia entre los resultados. Esto es: si el resultado A es preferido al B, entonces la utilidad U(A) es mayor que la utilidad U(B).

Cuando nos movemos en ambientes probabilísticos, una actuación suele desembocar en posibles resultados: eligiendo la estrategia, X tenemos una probabilidad p₁ de obtener el resultado A₁, una probabilidad p₂ de obtener el resultado A₂... y una p_i de obtener el resultado A_i. En este caso , una vez definida la función de utilidad de los sucesos A_i, la valoración de utilidad de la adopción de la estrategia o elección X será: p₁·U(A₁)+ ... + p_i·U(A_i), donde la suma de todas las p_i es lógicamente la unidad.
De esta forma, el ambiente de certidumbre se considera como una variedad del ambiente en riesgo, para el cual ante una determindad ectuación o estrategia, las probabilidades de todos los resultados posibles son cero excepto para uno de ellos, que vale uno: Hablamos de una distribución de probabilidad degenerada. Hablaremos pues de ambiente de riesgo, entendiendo que es el general que engloba al de certidumbre como caso particular.

John Von Neumann y Oscar Morgenstein establecieron la axiomática de las utilidad utilizando un concepto adicional: el de mixtura

Ante dos opciones X e Y, la mixtura de ambas se representa por pX+(1-p)Y. Aquí, tanto X como Y son actuaciones que llevan una distribución de probabilidad asociada de obtener los resultados A_i con probabilidades p_i la X y con probabilidades q_i la Y. La mixtura de ambas se interpreta como una decisión aleatoria consistente en elegir la actuación X con probabilidad p y elegir Y con probabilidad (1-p).

Existen cuatro axiomas de comportamiento racional que deben cumplir las mixturas. Cuando lo cumplen, el conjunto de todas las posibles decisiones junto con la operación mixtura se denomina un espacio de mixtura P.

Son los siguientes:

1.- Si X e Y pertenecen a P, entonces pX+(1-p)Y tambien pertenece a P.
2.- 1·X + 0·Y=X

3.- pX+(1-p)Y= (1-p)Y+pX

4.- Si Z= pX + (1-p)Y, entonces qZ + (1-q)Y = pqX + (1-pq)Y

En tal caso, la axiomática que nos ocupa consta de otros cuatro axiomas, que son los siguientes:

A I: Hay en P definidada una relación de preferencia-indiferencia que es un preorden completo.

A II: Hay definida en P una operación que lo convierte en un espacio de mixtura.

A III: Axioma de sustitución: Para cualquier X,Y,Z de P, X es preferida a Y si y solo si pX+(1-p)Z es preferida a pY + (1-p)Z.

A IV: Axioma de continuidad: Si X,Y,Z son tales que X es preferida a Y e Y es preferida a Z, entonces existen dos números p, q comprendidos entre cero y uno tales que:

pX + (1-p)Z es preferida a Y
Y es preferida a qX + (1-p)Z.

Cuando se cumple todo lo anterior, el teorema de existencia de función de utilidad, debido a Von Neuman y Morgenstein dice que existe una función U definida en el espacio de mixtura, única salvo por transformaciones lineales, lineal a su vez y que queda determinada fijando el valor de dos actuaciones.

Ramsey y grafos

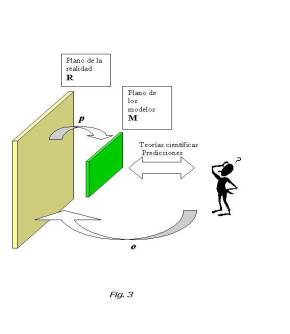
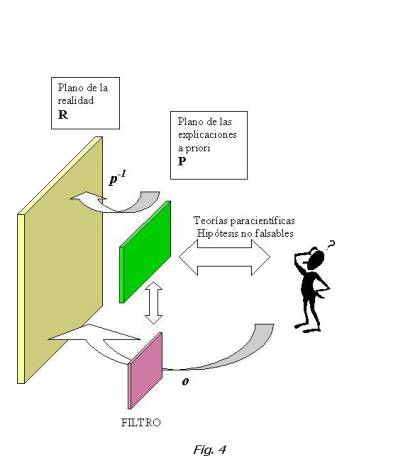
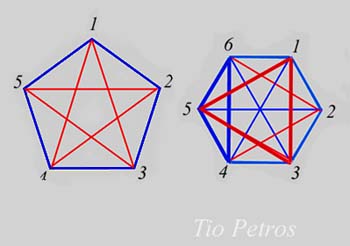Los últimos post del mes de Febrero trataban de explicar el enunciado (que no la demostración) del Teorema de Ramsey . Comentamos entonces que dedicaríamos varios comentarios a aplicaciones prácticas del mismo, para acabar de comprender el sentido profundo del teorema.

Para ello, vamos a apoyarnos en la teoría elemental de grafos. Un grafo no es más que una colección de puntos, junto con aristas que unen unos puntos a otros. Vamos a restringirnos a grafos simples no orientados, en los cuales los lazos entre puntos no tienen dirección, y no existen lazos múltiples entre la misma pareja de puntos; ni lazos que vayan de un punto al mismo punto. Cada arista por tanto une dos puntos, y es una buena representacione de una relación entre los mismos.

Un grafo es completo cuando toda pareja de puntos tiene una arista que los une. El grafo completo de n vértices se denomina K_n. En la figura tenemos dos grafos completos: K₅ y K₆. Sus aristas han sido coloreadas de dos colores: rojo y azul.

Veamos el siguiente enunciado:

En un grupo de seis personas, o se cumple que tres se conocen entre sí, o se cumple que tres no se conocen entre sí

En las figuras, cada persona del grupo es un punto, y las aristas representan la relación de conocimiento o desconocimiento mutuo entre ellos. Digamos que rojo indica que sí se conocen y azul lo contrario.

Una alternativa al enunciado anterior es la siguiente:

Si en un grafo completo K₆ coloreamos sus aristas de dos colores, siempre encontraremos un subgrafo K₃ monocolor.

Espero que sea evidente para el lector la equivalencia entre ambos enunciados, y espero también que aprecie el "sabor a Ramsey" de este último.

En efecto, tenemos una aplicación directa del teorema de Ramsey: tenemos un conjunto X de seis puntos; tenemos el conjunto de todos sus subconjuntos de dos elementos (R=2), que no son sino las aristas del grafo , y coloreamos todas ellas usando dos colores. Ahora, dados los números tres y tres , el teorema de Ramsey nos asegura que si el conjunto X es suficientemente grande, existirá en su seno un conjunto de tres puntos unidos tan sólo por aristas de color rojo, o un conjunto de tres puntos unidos tan sólo por aristas de color azul.

Las figuras nos demuestran que para el caso de cinco personas, no es obligado el cumplimiento. Es muy fácil demostrar que con seis sí. En el caso concreto que presento, aparecen regruesados dos subrafos de orden tres monocromáticos: los que tiene como vértices (1,3,5) rojo; y los que tienen como vértices (4,5,6) azul.

El Teorema de Ramsey nos dice que si el número es suficientemente grande, en un grupo habrá, por ejemplo 20 personas que se conozcan entre sí dos a dos, o 15 personas que no se conozcan mutuamente. Para cualquier par de números, existirá un número mínimo R(m,n;2) por encima del cual, un conjunto de personas tendrá en su seno m personas que se conozcan todas ellas dos a dos, y n personas que no se conozcan. R(3,3;2) = 6, como acabamos de ver. En general, los valores de los números de Ramsey son desconocidos; pero hablaremos de ello en próximos días.

Volvemos a poner el enunciado para animarles a releerlo. Seguramente ya no parece tan extraño como hace unos días...

Orden en el caos

Acabo de ver por la red aquí y aquí que hay gente que encuentra en las recientes fotos mandadas por las sondas robot Spirit y Opportunity , todo tipo de huesos, fósiles, huellas e incluso artefactos en el suelo marciano. La tendencia humana a encontrar pautas y organizaciones donde no las hay es un asunto interesante, pero de componente psicológica que trasciende por mucho el contenido de este blog. No obstante, a veces el orden, la estructura aparecen realmente. El autoengaño supone entonces pensar que este orden se debe a una causa extravagante; en nuestro caso, la existencia real de un dispositivo, o de un hueso en el suelo marciano. Todo esto me sirve de excusa para comentar lo siguiente.

El orden y la estructura pueden aparecer en la naturaleza por varios motivos ajenos a la inteligencia; humana, animal o divina. Uno de ellos es el imperativo termodinámico. Los cristales exhiben pautas ordenadas debido a consideraciones de equilibrio entre niveles de energía. Otras veces las pautas aparecen por simple casualidad. Y otras, por simple y pura necesidad matemática. Es de este tipo de orden matemáticamente necesario, que hace que el caos completo no pueda existir, del que vamos a hablar.

Iniciamos una serie de post sobre un tema difícil, que cae dentro de la combinatoria: el surgimiento de orden y pautas en conjuntos suficientemente grandes.

Algunas de las más interesantes ( y más recientes) contribuciones de la combinatoria son los denominados Teoremas de existencia.

Estos extraordinarios y difíciles teoremas aseguran la existencia de ciertos objetos matemáticos. En concreto aseguran la existencia de conjuntos en los cuales se cumplen determinadas relaciones o propiedades. El Teorema de Ramsey en concreto afirma que siempre aparecerá algo ordenado y con estructura en el seno de un conjunto, a condición de que dicho conjunto sea lo suficientemente grande.

Tras el enunciado (que veremos en post próximos), aparente ininteligible, como si de una cadena de símbolos sin sentido se tratara, se esconde el orden de una gran idea.

En una mágica recursividad éste es precisamente el mensaje del Teorema de Ramsey: el orden surge necesariamente en conjuntos suficientemente grandes. Nuestro teorema lo asegura, aunque por desgracia no nos dice lo grandes que deben ser dichos conjuntos.

Las implicaciones de todo tipo de este teorema son enormes en nuestra vida cotidiana, y explica ciertas regularidades que observamos en la naturaleza, que no tienen otra explicación: en virtud del teorema de Ramsey encontramos aparentes pautas en sucesos absolutamente aleatorios. Este tema es importante, porque no estamos hablando de teoría de probabilidades, sino de combinatoria.

¿Qué pretendo decir con esto último? Muy sencillo. Al estar totalmente desligado del cálculo de probabilidades, el teorema de Ramsey nos habla de necesidad de cumplimiento de determinados patrones extraños, no de la probabilidad de existencia de los mismos. La extrañeza de los mismos no es, por supuesto, una característica intrínseca de dichos patrones, sino una medida de nuestra incapacidad para percibir su presencia como necesaria, incapacidad que nos incita a engañarnos. El engaño consiste en imaginar motivos o incluso voluntades inteligentes detrás de las pautas observadas.

La amplitud de campos en los que el teorema se aplicable es infinito, desde estrellas que parecen adoptar configuraciones animales o humanas en la bóveda celeste hasta grupos de personas que se reúnen en torno a una mesa, ...

Lo primero que haremos es hablar de su descubridor: un extraordinario ser humano que se llamó Frank Plumpton Ramsey , y que murió a la tempranísima edad de 26 años.

Espero contar con su atención en los próximos días...el paseo que les propongo me parece bastante más interesante que intentar encontrar cosas raras en las fotos del suelo marciano.

Números sociables

Las propiedades de un número en principio no son atributos que dicho número exhibe con independencia de las que puedan exhibir otros números: prácticamente todas las propiedades de un número lo son por la relación con otros números. Por ejemplo: la primalidad de un número está establecida por la ausencia de división entera con otros números menores que él. Por lo tanto, tenemos un mundo de relaciones entre números, relaciones entre parejas, o en general entre n-tuplas de números.

La relación binaria entre enteros más común es la de primalidad mutua: dos números son primos entre sí cuando no tienen divisores comunes, además de la unidad.

Vamos a hablar hoy de una relación entre números que trasciende la relación binaria, y que puede englobar, en principio a cualquier cantidad finita de enteros: la sociabilidad .

Para ello introduciremos en concepto la función aritmética suma de divisores .

Una función aritmética es una función que toma valores reales o complejos, cuyo campo de difinición es el conjunto N. Muchas de las funciones aritméticas dependen mucho más de la descomposición en factores primos del argumento que que valor numérico del mismo. Esto hace que su comportamiento sea muy errático y difícil de estudiar.

La función S(n) se define como la suma de los divisores de n. Como pueden ver, nada misterioso ni difícil de entender. Como los divisores de ocho son el propio ocho, el cuatro, el dos y el uno, S(8)=8+4+2+1=15.

Como un primo no tiene más divisores que el propio número y la unidad, S(p)=p+1, para p primo.

En lo que sigue, vamos a referirnos siempre a la suma de divisores propios: exceptuado el propio número. Para evitar confusiones denotaremos S (mayúscula) a la suma de todos los divisores, y s (minúscula) a la suma de los divisores propios..

Con n = 20: Los divisores propios de 20 son 1, 2, 4, 5 y 10. s(20) = 1 + 2 + 4 + 5 + 10 = 22. Como el resultado es mayor que el número inical, se dice que 20 es un número abundante .

Si hacemos lo propio con el 22, resultado de la operación anterior, obtenemos: s(22) = 1 + 2 + 11 = 14, la suma es menor que el número escogido; se dice que 22 es un número defectivo .

Continuando, si seguimos calculando la s(n) para cada suma obtenida, tenemos:

s(14) = 1 + 2 + 7 = 10;
s(10) = 1 + 2 + 5 = 8;
s(8) = 1 + 2 + 4 = 7;
s(7) = 1 porque 7 es primo,
y s(1) = 0 porque 1 no tiene divisor propio.

Se ha obtenido así una sucesión finita: 20 , 22 , 14 , 10 ,8 , 7 , 1 , 0.

Otra sucesión es : 24 , 36 , 55 , 17 , 1 ,0.

Nada obliga a que la sucesión sea finita, pues pudiera ocurrir que fuera periódica. Si el período fuera uno( el mismo número se repite siempre), estaremos en el caso de que s(n)=n. Todo número que cumple dicha ecuación se denomina número perfecto.

Número perfecto es aquel igual a la suma de sus divisores propios

De ellos, y de la caracterización para los perfectos pares hablamos en su momento aquí.

De los números perfectos impares nada se sabe, ni siquiera su existencia o inexistencia.

Cuando el período de la sucesión anterior es igual a dos, tenemos el caso de números amigos :
Dos números son amigos cuando cada uno es igual a la suma de divisores del otro

La pareja (220, 284) es una pareja de números amigos, como podemos comprobar:

s(220) = 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284 y
s(284) = 1 + 2 + 4 + 71 + 142 = 220.

Luego la sucesión que comenzara con uno de ellos sería:

220, 284, 220, 284, 220, 284, 220, 284... de período dos.

Leo por la red que “En la Edad Media, existió la creencia de que si se daba de comer a dos personas (al mismo tiempo pero no en el mismo lugar) sendos alimentos que contenían una inscripción 220 para uno y de 286 para el otro, entonces se volvían amigos por arte de magia.”

Otras parejas de números amigos son (1184; 1210), (2620; 2924), (5020; 5564) y (6232; 6368), (17296; 18416) y (9363584; 9437056).

En general, se llaman números sociables a las n-tuplas de números de una sucesión así formada de período n.
He podido encontrar por ahí los siguientes:

(12.496, 14.288 , 15.472 , 14.536 , 14.264 ) Cinco enteros, cada uno es igual a la suma de los divisores propios del anterior, y el primero respecto al primero.

En esta dirección teneis un programa en Mapple para generar secuencias de sumas de divisores propios, así como la información que he utilizado de base para elaborar este post. Por lo demás, poca información parece que hay, al menos fácil de encontrar sobre esta generalización de los números amigos.

Fundamentando la matemática en el vacío.

A lo largo de los tres post anteriores hemos visto cómo los matemáticos del siglo XX intentaron buscar los fundamentos de su disciplina con la máxima economía de conceptos, hasta llegar al paroxismo: el conjunto vacío se revelaba como la piedra angular de todo el edificio numérico.

Nos quedaba definir el conjunto N. Pero eso ahora es cosa trivial: el conjunto N es el único conjunto que contiene al conjunto vacío y a todos sus sucesores; y sólo a ellos. La formulación de los enteros sobre el esquema aquí esbozado de los naturales; la de los racionales sobre los enteros y la de los números reales como clases de equivalencia de sucesiones de Cauchy de racionales nos da un panorama completo de la construcción numérica hoy aceptada por la comunidad matemática.

Este es un buen momento para ver desde otro punto de vista la aritmética transinfinita de Cantor, tema que tocamos en los artículos sobre el Aleph y sobre las sucesiones de Goodstein.

En efecto, hemos visto que un número natural se define como el conjunto de todos sus anteriores:

n={0,1,2,3,...,(n-1)}

Nada nos impide considerar el conjunto N como un infinito actual y hacerle corresponder un número infinito (el menor número infinito) que sería:

w={0,1,2,3,...}=N

Digo que nada nos impide efectuar esta consideración porque ya tenemos perfectamente definido el conjunto N, y por lo tanto estamos legitimados para usarlo como un objeto actual, en su totalidad.

Pero ahora nada nos impide continuar:

w+1={0,1,2,3,...,w}=N U {w}

w+2={0,1,2,3,...,w,w+1}=N U {w,w+1} ...

Tenemos así las bases de los ordinales transinfinitos de Cantor, que surgen con la mayor naturalidad de la teoría de conjuntos mientras que vistos "a pelo", como los habíamos visto en los post anteriores, parecen un poco extraños.

Dejaremos por ahora este apartado tan elemental ⁽¹⁾de la matemática para adentrarlos en otros paisajes a partir del lunes. Con su compañía, por supuesto.

(1): En matemáticas, la palabra "elemental" y la palabra "básico" son dos palabras con acepciones diferentes a las del lenguaje ordinario. Indican que el tema tratado se refiere a las bases y/o fundamentos de la matemática, no a su poca dificultad. De hecho, los temas elementales y básicos suelen ser de gran dificultad.

¿Qué es un número? (3)

Continuamos con lo prometido. Tenemos definido el conjunto vacío, lo cual pueda parecernos poca cosa, pero eso es todo con lo que tenemos que trabajar si no queremos introducir axiomas adicionales.

Miren los dos teoremas de la ilustración, y no se asusten: es mucho más fácil de lo que parece a primera vista. Tenemos dos teoremas, que no es lo mismo que dos axiomas. Los teoremas se demuestran; aunque demostrar estos es una tontería, de puro fácil. El primero es el teorema del par no ordenado . Nos dice que dados dos conjuntos (¡Qué lujo!, les recuerdo que de momento sólo estamos legitimados para usar un conjunto: el vacío: el único que hemos definido), decía que dados dos conjuntos, existe un conjunto de dos elementos, que son precisamente los dos conjuntos anteriores.

Cómo podemos demostrar esto? Pues usando el axioma de formación. Dado que la descripción que utiliza el enunciado del teorema es una descripción precisa, el axioma nos asegura que existe tal conjunto; y el axioma de igualdad nos asegura que dicho conjunto es único, luego ya tenemos demostrado el teorema.

Es importante entender que el nuevo conjunto tiene a los dos iniciales como elementos, de forma que tiene DOS elementos, independientemente de los elementos de los dos conjuntos iniciales.

Lo mismo vale para el teorema de la unión: dados dos conjuntos existe un conjunto cuyos elementos son los de los dos conjuntos (los de uno, los del otro o los de los dos).

Es importante comprender que utilizando estos dos teoremas no estamos utilizando nada nuevo, que no salga de los dos axiomas iniciales.

Dado que de momento sólo tenemos el conjunto vacío, podemos utilizar el teorema 1 haciendo los dos conjuntos iniciales sean el mismo. Dada la generalidad del teorema (empieza por “para todo z , u”, verdad?), esto no supone violación alguna del teorema.

Qué obtenemos? Pues el teorema ahora nos dice que si existe un conjunto A, entonces existe un conjunto {A}, con un único elemento, que es precisamente el conjunto A. Es crucial ver que los conjuntos A y {A} son radicalmente diferentes: si A={a,b,c,d,e}, por poner un ejemplo, A tendría cinco elementos, que son a,b,c,d y e. Sin embargo {A} tiene un único elemento, que es A, o que es {a,b,c,d,e}. Este nuevo conjunto lo llamaremos unitario del conjunto A .

De modo que ahora no sólo tenemos el conjunto vacío, sino también el conjunto {vacío}, que ahora tiene un elemento.

Estamos en condiciones de definir el sucesor de un conjunto A , como la unión de dicho conjunto con su unitario: suc (A)= A U {A}. El teorema de la unión nos asegura su existencia, y el axioma de igualdad su unicidad, de modo que está bien definido.

Supongo que mis lectores habrán adivinado la estrategia a seguir:

Definimos el cero como el conjunto vacío. No hay circularidad alguna en ello, ya que hemos definido el conjunto vacío en el post anterior sin hacer para nada uso del concepto cero.
Una vez definido el cero, definimos el sucesor de un número como el sucesor del conjunto con el cual hemos identificado dicho número.
Lo vemos en la ilustración siguiente:



Hemos sido capaces de definir los números naturales sin hacer uso previo de ningún concepto numérico, y sin usar los axiomas de Peano, que ahora admiten demostración: vemos que todo número es sucesor de alguno, excepto el cero, que no lo es de nadie. Podemos demostrar que dos números diferentes tienen sucesores diferentes...

Hemos construido las bases de la matemático desde el vacío más absoluto. Cualquier adepto al zen estaría muy contento: belleza y armonía en su máxima simplicidad; minimalismo conceptual y elegancia absoluta. A partir de este momento, deberíamos decir, con permiso de Kronecker: “Dios creo el conjunto vacío; el resto es obra del hombre” .

Hemos dicho que ahora ya podemos demostrar los axiomas de Peano desde esta nueva teoría. Esto no es exactamente así: hemos definido los números naturales, pero nos falta definir correctamente el conjunto N. No obstante, la tarea está ya casi terminada.

¿Qué es un número?

No parece que exista disciplina científica cuyo objeto sea tan difícil de precisar como la matemática. Precisamente por ello es doblemente importante establecer un buen punto de partida: unas bases desde las que edificar el edificio entero.

Históricamente las bases iniciales fueron geométricas. La matemática griega era básicamente la ciencia de las figuras geométricas. En el siglo III antes de nuestra era Euclides propuso un sistema riguroso basado en unos pocos postulados (cinco axiomas), desde los cuales edificar toda la teoría geométrica con el auxilio de las leyes de la lógica de primer orden. Las afirmaciones cuya veracidad se probaba a partir de los axiomas eran teoremas.

Estas bases permanecieron firmes hasta el siglo XVII, en el que Newton y Leibniz desarrollan el cálculo, atendiendo a demandas concretas de la física del momento. Las nociones de límite en las que se basaban suponía una “desgeometrización” de la teoría matemática, aunque aún las derivadas eran concebidas como pendientes y las integrales como áreas: se notaba la influencia geométrica de antaño. Cuando Cauchy y Weierstass, hacia 1.870 reformulan las definiciones de límite sin el auxilio de las incómodas cantidades que “tienden a cero”; cuestión que nadie entendía en realidad, y consiguen la definición épsilon-delta que usamos actualmente, el cálculo llega a su mayoría de edad, y el concepto geométrico queda sustituido por el concepto de número (número real, concretamente).

Pero la cosa no paró ahí: las verdaderas bases debían ser más generales que los números reales. Existe una maravillosa historia que cuenta cómo los números reales son construidos desde los racionales, utilizando sucesiones de racionales (sucesiones de Cauchy); los racionales desde los enteros, y los enteros desde los naturales.

Kronecker diría, resumiendo la situación: Dios creó los números naturales, el resto es obra del hombre

Estos números naturales surgían como entidades radiantes, primigenias de un puñado de axiomas: los cinco axiomas de Peano :


1.- 0 es un número
2.- El siguiente de todo número es un número
3.- Números distintos tienen siguientes distintos
4.- 0 no es el siguiente de ningún número
5.- Si una determinada propiedad es cumplida por el 0, y si es cumplida por un número también es cumplida por el siguiente, entonces es cumplida por todo número.

Parecería que estos cinco axiomas concentran la totalidad de la matemática, dado que desde ellos se puede construir todo... y sin embargo no es así.

Volvieron a cambiar las bases, y así como de los objetas geométricos pasaron a los números reales y de estos a los naturales, ahora las bases se trasladaban a una teoría nueva que surgía de la mente de George Cantor : la teoría de conjuntos.

Esto supone que los números naturales; el cero, el uno, el dos, etc deben ser definidos en base a conceptos aún más generales.

Sin embargo, esto no parece cuestión fácil: ¿cómo definir el cero sin caer en una peligrosa circularidad introduciendo el concepto a definir en la definición?

No parece fácil. Decir que el cuatro es el conjunto de todos los conjuntos de cuatro elementos no es serio, por motivos que saltan a la vista.

Cómo podemos definir un número natural desde la teoría de conjuntos de forma que no caigamos en una circularidad inaceptable?

Lo vemos próximamente...

Base matemática de la música ( y 3 )

PRECISANDO LA NOCION DE DISTANCIA

Este es un buen momento para introducir el concepto de distancia, de forma tan general que sea aplicable tanto a distancias ordinarias entre puntos del espacio como a distancias entre notas musicales, o entre diferentes apuestas de un sistema de quinielas.

Previo a la necesidad de tal concepto, tenemos un conjunto X de objetos entre los cuales queremos difinir algo que pueda llamarse distancia.

El producto cartesiano X x X no es sino el conjunto de todos los pares de objetos de X de la forma (a,b). Pues bien; una distancia es una aplicación de X x X en R (conjunto de los reales), d: X x X -------- R que cumpla cuatro propiedades:

1.- d(a,b) mayor o igual que 0
2.- d(a,b)=0 si y solo si a=b
3.- d(a,b)=d(b,a)
4.- d(a,b) menor o igual que d(a,c)+d(c,b)

Por lo demás, tenemos plena libertad para elegir la función d. A partir de ahora consideraremos que las letras que representan notas en realidad representan las frecuencias en herzios de dichas notas. Para medir las distancias entre notas musicales, la función d(a,b)=b-a no es interesante. Hemos visto que es la relación de frecuencias la importante, no su diferencia. Dos notas con relación doble- mitad tienen la misma distancia según nuestra percepción (una octava), sin importar los valores absolutos de frecuencia de ninguna de ellas. Por lo tanto la distancia que nos interesa debe ser de la forma d(a,b)=b/a. Como para el caso de que a y b sean iguales la distancia debe ser cero (primera propiedad). Dado que el logaritmo de 1 es precisamente 0, y dado que las leyes logarítmicas son las que mejor se adaptan a la sensibilidad de nuestros sensores, tomaremos como función distancia:

D(a,b)=K. Abs( Log (b/a))

La K no es sino una constante de escala, sin la menor importancia teórica, aunque sí práctica como veremos. He tomado el valor absoluto del logaritmo para que se cumpla la propiedad 1. Como sabemos (ahora lo sabemos, porque ya hemos leído los dos post anteriores, verdaaaaaaad?) que una octava tiene 12 semitonos, si tomo K=1200/log(2), entonces un Do estará del Do inmediatamente superior a una distancia de:

(1200/log(2)) . log(2)=1200 unidades,

que llamaremos cents , y por lo tanto un semitono de la escala temperada, que era la que dividía la octava en doce intervalos idénticos, tendrá 100 cents. Un tono temperado 200, etc, etc.

Quede claro que los cents no son una unidad de frecuencia, de tono ni nada parecido: son una unidad de separación entre tonos.

Podemos calcular ahora cuántos cents tiene un intervalo de quinta justa, que es el que hemos utilizado para construir nuestra escala de posts anteriores.

quinta justa = log 3/2 x 1200/log2 = 701,955 cents

Recordemos que, por definición:

octava justa= 1200 cents.

Habíamos visto que doce quintas justas no eran idénticas a siete octavas. Efectivamente:

12 quintas= 12 x 701,955 = 8.423,46 cents
7 octavas = 7 x 1200 = 8.400 cents

La diferencia es exactamente el déficit de la quinta del lobo del post anterior, y se denomina coma pitagórica .

1 coma pitagórica= 23,46 cents

Así pues, todo el misterio está en repartir estos casi 23 cents y medio entre las doce quintas, en función de qué es lo que queramos conseguir. Si queremos facilidad en la afinación de instrumentos, y no somos muy exigentes (eso es exactamente lo que pasa con la música actual), repartimos equitativamente: 23,5/12= 1,95 cents por quinta; valor que aproximaremos a 2 cents por quinta. De esta manera, ninguno de los intervalos entre notas será perfecto (expresable por una de esas fracciones de pequeños números, que producían un gran equilibrio entre las ondas senoidales de ambas notas). Un oído entrenado lo notará.

Las otras posibles soluciones? Pues pasan por el compromiso de “destrozar” cierto número de quintas justas y dejar perfectas las demás. Una solución es la de Valotti, que consiste en elegir seis de las doce quintas y distribuir en ellas una coma pitagórica (4 cents por quinta elegida)



Otro sistema, llamado Werckmeister III lo hace tomando cuatro quintas y restando seis cents a cada una de ellas:



Por último, el sistema Kirnberger reparte 11 cents entre dos quintas consecutivas, dejando los 2 restantes para otra:



Cada uno de ellos tiene una razón de ser, presenta sus ventajas y sus desventajas, pero estas profundidades musicales exceden los límites de Tio Petros (entendiendo por Tio Petros tanto el blog como su autor).

Base matemática de la música (2)

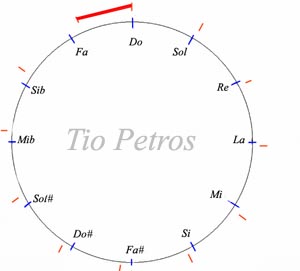Según veíamos en el post anterior, las escalas musicales occidentales antiguas se construyeron en torno a la idea de producir la máxima consonancia posible; cosa que ocurría cuando la relación de las frecuencias de dos tonos tocados simultáneamente era expresable mediante una fracción lo más simple posible. Dado que un tono base y otro de frecuencia doble dan la sensación del mismo tono pero más agudo, lo natural era considerar esa distancia como la total que había que subdividir; independientemente de que pudiera adjuntarse otra hasta la frecuencia triple, cuádruple, etc...

La fracción más simple posible es la de 3/2, que es la que usábamos para crear nuevas frecuencias a partir de la de origen, que llamaremos tónica . Si la tónica es un Do , al multiplicarla por 3/2 obtendremos un Sol . Este intervalo se denomina una quinta justa. (Esta denominación tiene mucho sentido: para llegar del Do al Sol hay que pasar por cinco notas: DO, Re, Mi, Fa, Sol; ambas incluidas. Por supuesto, una vez que tengamos construida la escala!!!)

Pues bien, decíamos que a base de quintas justas íbamos construyendo las demás notas de la escala. Cuando obteníamos valores superiores a 2, nos salíamos de la escala ( la nota obtenida era más alta que el Do superior al que queríamos llegar), con lo que simplemente dividíamos por dos, y volvíamos a caer en nuestro dominio a subdividir. Se trata de una operación módulo una octava.

Dado que el 2 y el 3 son primos entre sí, no podemos tener esperanza alguna de llegar jamás al Do superior exactamente: iríamos obteniendo infinitas notas por este procedimiento, todas entre ambos Do, de modo que debemos cerrar el círculo de quintas en falso. Efectivamente, alguna vez obtendremos un valor lo suficientemente cerca del Do alto como para asimilarlo.

Esto ocurre tras 12 quintas , más sus respectivas correcciones (dividiendo por dos) para no salirse del intervalo. Efectivamente, 12 quintas suponen siete correcciones ( no hay más que ir obteniendo los valores para comprobarlo) 3¹²/2¹⁹= 531441/524288=1,0136.

Si vemos la figura, tenemos sobre un círculo de quintas marcados los doce intervalos equidistantes (escala temprada) con segmentos azules, mientras que las notas obtenidas por el método aquí indicado están en rojo. Dado que las 12 quintas son algo mayores que las siete octavas, para cerrar el círculo en falso debemos aceptar el último intervalo (marcado en rojo) bastante más pequeño que los demás. Esta quinta irregular es denominada la quinta del lobo . Cada una de las doce notas obtenidas son las de nuestra escala cromática. El problema que tenemos ahora es ver si podemos distribuir de alguna manera esta diferencia notable de la quinta del lobo entre varias. La solución de repartir equitativamente entre todos los intervalos ( que es lo que hacemos nosotros con nuestra escala actual, o escala temperada) no les gustaba nada a los antiguos, que eran más exigentes y estetas que nosotros, por motivos obvios: nos cargamos todas las quintas justas y ya no existen consonancias perfectas.

Este es un problema sin solución óptima. Hay que optar entre varias soluciones, llamadas temperamentos . Se trata de dividir el déficit de la quinta del lobo entre algunos intervalos, de forma que se mantenga dentro de lo posible la perfecta armonía de 3/2 entre varias quintas.

Para ver cómo lo consiguieron, necesitamos más teoría, que será la semana que viene.

Que tengan mis lectores un buen fin de semana.

Base matemática de la música.

Estarán de acuerdo conmigo en que no hace falta saber matemáticas para disfrutar de la música. De hecho, a simple vista parecen ser dos temas totalmente desligados... pero en realidad muy pocas cosas están desligadas de la matemática.
¿Saben ustedes porqué las notas son siete? No parece un número muy adecuado; al fin y al cabo es primo, y no tiene divisores; parecería que ocho es más “adecuado”.

En realidad las siete notas DO, RE MI FA SOL LA SI (escala diatónica) se convierten en doce si intercalamos notas intermedias, obteniendo doce, que constituyen la llamada escala cromática: Do, Do#, Re, Re#, Mi, Fa, Fa#, Sol, Sol#, La, La#, y Si. El símbolo # se llama sostenido, e indica un tono (una frecuencia) intermedio entre la nota que lo nombra y las siguiente. En solfeo se aprende que además existen los bemoles (b), que disminuyen el tono en lugar de aumentarlo, de forma que Re# = Mib y La#=Sib, por poner dos ejemplos.

No se trata de una arbitrariedad, ni mucho menos. Existe una base clara que apoya tal “dodecafonismo”. El propósito de este post es intentar explicarlo.

Dos sonidos puros simultáneos pueden dar una sensación agradable (consonante) o no tan agradable (disonante). El asunto depende de la relación entre sus frecuencias. La consonancia perfecta, y obvia, si produce cuando ambos tonos tienen la misma frecuencia (unísono). Para el resto de los casos, el resultado será más consonante cuando al relación de frecuencias sea un número racional de denominador pequeño. En el fondo todo el misterio es la suma de funciones senoidales: si una frecuencia es 2/3 de otra, la suma “encaja” mucho mejor que si es 465/422...

Es obvio que después del unísono, la mejor consonancia es cuando una frecuencia es el doble de la otra. La sensación percibida es que son ambas la misma nota, pero una más aguda que la otra. Por ello, ambas reciben el mismo nombre (se dice por motivos que veremos que están a una octava de distancia).

¿Cómo dividimos las “distancia entre dos notas del mismo nombre, de frecuencias f y 2f? Pues lo más racional parece seguir con fracciones sencillas. Si tomamos una frecuencia 3f/2, obtenemos una nueva nota, de composición sumamente agradable con f y con 2f.

El siguiente paso parece natural: tomar una frecuencia que sea 3/2 de la última; osea 9/4 de la frecuencia base. El problema es que esta fracción es mayor que dos, por lo que nos habremos salido por encima de 2f. Lo corregimos con bajarla una octava ( dividir la frecuencia por dos), que como hemos dicho da la misma sensación de nota musical, si bien más grave), y tenemos 9/8.

Repitiendo el proceso, tenemos:
· f
· 3/2·f
· 9/8 ·f.(Después de haber descendido una octava).
· 3/2·9/8 ·f=27/16·f
· 3/2·27/16 ·f=81/32·f. (Como la frecuencia es más grande que 2f, descendemos una octava y obtenemos 81/64·f)
· 3/2·81/64 ·f=243/128·f
Si ordenamos de menor a mayor estos seis valores, tenemos:

Nota Base f
9/8·f
81/64 ·f
Quinta 3/2·f
27/16·f
243/128·f
Octava 2·f

Tenemos un buen motivo para pararnos con seis valores, y es que si calculamos los cocientes de cada frecuencia con la anterior, nos sale lo siguiente:

(9/8):1=9/8__________________1,125
(81/64):(9/8)=9/8____________1,125
(3/2):(81/64)=32/27__________1,185
(27/16):(3/2)=9/8____________1,125
(243/128):(27/16)=9/8________1,125
2:(243/128)=256/243__________1,053

Vemos que, salvo el salto del tercero al cuarto tono, la cosa está muy equilibrada. Curiosamente, en este hueco entre el tercero y el cuarto se encuentra la fracción 4/3. Si lo intercalamos obtenemos la siguiente tabla:

Frecuencia___________ Razón nota anterior _____________Nombre

Tónica_____f_____________________________________________Do
Segunda 9/8·f___________9/8=1,125_________________________Re
Tercera 81/64·f__________9/8=1,125_________________________Mi
Cuarta 4/3·f_____________256/243=1,053_____________________Fa
Quinta 3/2·f_____________9/8=1,125_________________________Sol
Sexta 27/16·f___________9/8=1,125__________________________La
Séptima 243/128·f________9/8=1,125_________________________Si
Octava 2f_______________256/243=1,053_____________________Do

Hemos obtenido una división de la octava (de un Do grave a un Do de doble frecuencia) atendiendo a criterios de máxima consonancia, por lo que las combinaciones de sonidos serán lo más agradable posible. Podemos comprobar que las distancias Mi-Fa y Si-Do son menores que el resto (empleamos en este contexto la palabra distancia en una acepción no habitual: como cociente de frecuencias) . De hecho, las distancias Mi-Fa y Si-Do son aproximadamente la mitad, habida cuenta de que 1,053 ² se aproxima bastante bien a 1,125.

Llamamos entonces a la distancia entre dos notas consecutivas cuya relación de frecuencias es 1,125 y semitono a la distancia referida a un cociente de frecuencias de 1,053. Con esto presente, entre dos notas consecutivas hay siempre un tono, con la excepción de las distancias Mi-Fa y de Si-DO, intervalos de un semitono.
Si bien este estado de cosas parece bastante complicado, la realidad (por una vez) es más sencilla. Actualmente se usa la llamada Escala temperada , que consiste en formar la escala cromática de las doce notas mencionadas más arriba a base de multiplicar la frecuencia de la tónica por la raíz doceava de dos. Obtenemos una escala promediada que vuelve a la tónica una octava más alta, con doble frecuencia tras pasar por las doce de la escala. En la escala temperada , los múltiplos perfectos de frecuencias se pierden, y las armonías no son tan redondas, pero se simplifica enormemente la tarea de afinación de instrumentos musicales. Simplificación ramplona a juicio de los amantes de la música antigua.

En la siguiente imagen podeis comparar la escala temperada, completamente fría y perfecta con otras escalas:

Escala temperada

Shree (india)

Hirajoshi (Japón)

Diatónica o pitagórica