Conceptos

Paradojas infinitodimensionales ( y 2)

Las respuestas dadas a la paradoja del post anterior por Eratóstenes y Tute son muy satisfactorias, y completamente correctas. Vamos a verlo en este post desde otro punto de vista que nos ayudará a tomar contacto con algunas nociones que necesitaremos para hablar algún día de los Espacios de Hilbert .

Cuando queremos definir un punto de un espacio de n dimensiones, debemos dar n valores, que son las n coordenadas que se necesitan para ubicar dicho punto en el espacio. La distancia euclídea de dicho punto al origen nos viene dada por el teorema de Pitágoras: será la raíz cuadrada de la suma de los cuadrados las n componentes.

De esta forma, podemos establecer una aplicación entre el conjunto de puntos del espacio y el conjuntos de números reales, de forma que a cada punto le corresponde el valor numérico de su distancia al centro. Si consideramos cada punto como un vector que nace en el origen y llega a dicho punto, dicho número se denomina norma del vector, y la aplicación se denomina norma del espacio, que ahora se dirá espacio normado. Existen otras normas que no son la euclídea, pero deberán cumplir una buenas propiedades para merecer tal nombre. Otro día hablaremos de ellas.

Un subconjunto del espacio se dice acotado si cabe dentro de una esfera maciza de radio suficientemente grande. Dicho de otra manera: si todos sus puntos están a una distancia no infinita del origen. (aquí el origen es arbitrario: podríamos decir si todos sus puntos están a una distancia no infinita de un punto dado).

Podeis observar que en el espacio de infinitas dimensiones tenemos una interpretación muy intuitiva de qué es cada “punto”: es una sucesión de infinitos números reales, sus coordenadas. Llegamos a la conclusión de que para que un punto esté a distancia no infinita del centro debe cumplirse que la suma de los cuadrados de sus coordenadas sea finita, pues sólo en este caso será finita la raíz cuadrada de dicha suma, y por tanto la distancia al origen. Esto ocurre por ejemplo para aquellos puntos que tengan todas las coordenadas igual a cero salvo un número finito de ellas, pero también puede ser que todas ellas sean diferentes de cero: debemos poner pues la restricción de que la serie que surge del sumatorio de los cuadrados de sus coordenadas sea convergente. Esta restricción es muy importante en los llamados Espacios de Hilbert , por ejemplo.

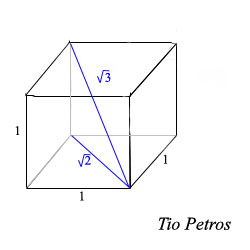
Si veis la definición de cubo macizo en este espacio, veremos que los puntos interiores tienen la restricción de que cada una de sus coordenadas es menor o igual a un número dado en valor absoluto. Los puntos que tengan todas el valor absoluto de sus coordenadas iguales a dicho valor son precisamente los vértices del cubo, si tenemos n dimensiones, como cada vértice puede tener cada una de sus coordenadas positivas o negativas, tenemos 2 ⁿ posibilidades, que nos da el número de vértices de dicho cubo.

En infinitas dimensiones, y pensando en el cubo de arista dada, infinitos son los vértices, pero en todos ellos el cuadrado de cada coordenada vale una cantidad no nula y mayor que cero ( al elevar al cuadrado (+z) ó (-z) obtenemos siempre una cantidad positiva); y la suma de todos estos cuadrados es infinita, luego cada uno de los vértices está a infinita distancia del origen. Poco importa que el tamaño de la arista: siempre que sea mayor que cero, obtenemos un objeto no acotado que no puede caben en esfera alguna.

Esto no ocurre para ningún valor del número de dimensiones del espacio, por grande que sea mientras sea finito; sólo ocurre para los espacios infinitodimensionales.

Por lo tanto, el error estaba en dar por buena la existencia de un cubo inscrito en la esfera.

Cosas de los espacios infinitodimensionales

Nos es imposible visualizar un espacio de más de tres dimensiones, y sin embargo no tenemos ningún problema para trabajar con espacios de más dimensiones. Muchas veces, la extrapolación a mayor número de dimensiones es tan trivial, que en los libros de texto se omiten los detalles...
La cosa cambia sin embargo de forma drástica cuando el número de dimensiones es infinito.
Vamos a comentar una aspeto curioso y sorprendente de dos cuerpos infinitodimensionales: la esfera y el cubo.

No nuestra esfera ni nuestro cubo (hexaedro), ciertamente, sino el equivalente en espacios de dimensiones cada vez mayores, hasta llegar al infinito numerable.

Una esfera se define en cualquier espacio como el conjunto de puntos que equidistan de otro dado. Pasaremos por alto el "detalle" de que debemos tener definida una distancia entre cada pareja de puntos, y supondremos que estamos hablando de la distancia euclídea normal; esa que todos conocemos.

En dos dimensiones tenemos círculo, que es una superficie plana. En tres, tenemos la esfera de toda la vida; una superficie cerrada en forma de balón. Para treinta y cinco dimensiones, la definición es la misma; a pesar de que seamos incapaces de visualizar el objeto.

Un cubo unidad lo podemos definir como el conjunto de puntos generados por vectores unitarios de una base ortonormal del espacio, mediante combinaciones lineales en las que los coeficientes van de cero a uno. Este galimatías no quiere decir otra cosa que lo que todos ustedes saben: dado un punto de origen, que será uno de los vértices del cubo, dibujamos tantas flechitas perpendiculares entre sí como dimensiones tengamos, y ya tenemos las aristas del cubo que convergen en ese vértice... lo demás es dibujo lineal.

Pues bien: ¿Cuál es la longitud del mayor segmento que cabe dentro de un cubo y dentro de una esfera?

Para una esfera, es evidente que el mayor segmento pasa por el centro, y tendrá una longitud de dos veces el radio. Eso sucede con la esfera de en un espacio de dos dimensiones(círculo), y con la esfera en un espacio de tres (nuestra esfera de toda la vida). Por la propia definición de esfera, no importa la dimensión del espacio, del centro a cualquiera de sus puntos la distancia es constante e igual al radio, y el mayor segmento que cabe en el interior es un diámetro, de longitud doble al radio.

¿Y qué sucede con el cubo?

Pues la sorpresa es que el cuadrado, el cubo y las demás figuras correspondientes a máyores dimensiones tienen diagonales, cuyas longitudes son mayores que los lados. Para el cuadrado, la diagonal vale raiz de dos, y para el cubo vale raíz de tres. Una diagonal en un hipercubo n-dimensional mide raíz de n, que es una función creciente de n, y por lo tanto, en un espacio de infinitas dimensiones dentro de un cubo cerrado CABE UNA RECTA INFINITA.

La proyección estereográfica de Riemann

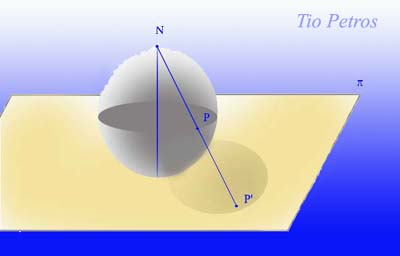Un lector me pregunta por la equivalencia topológica entre la esfera y el plano. Intuitivamente, parece ser que ambas superficies no son equivalentes. Después de todo, la esfera es una superficie muy diferente a un plano; no sólo por su forma (cosa poco importante en topología) sino por propiedades globales, como acotamiento.
En efecto, ambas superficies son distintas a nivel topológico. Lo que ocurre es que basta con eliminar un punto a la esfera para que dejen de serlo.
Supongamos una esfera descansando sobre un plano. Llamaremos punto S (sur) al único punto de contacto entre ambos, y punto N (norte) a la antípoda del punto S. Haremos corresponder cada punto P de la esfera con cada punto P’ del plano de la siguiente forma: unimos el punto N de la esfera con el punto P, y prolongamos la recta de unión hasta que corte al plano. Ese punto de corte es el punto P’, imagen de la proyección.
Es fácil darse cuenta de que cada punto de la esfera tiene su fiel reflejo en el plano, y viceversa; si exceptuamos el propio punto N, que no tiene correspondencia. Esta proyección se denomina proyección estereográfica de la esfera en el plano, o proyección de Riemann .
Los círculos de la esfera paralelos al ecuador se convierten en círculos en el plano con centro en el punto S, pero no se respetan las distancias (después de todo, la topología es lo que queda de la geometría cuando hemos suprimido la noción de distancia! ): cuanto mayor latitud norte tenga el paralelo, mayor es el radio del círculo proyectado en el plano. Un minúsculo paralelo muy cercano al punto N tendrá como reflejo un enorme círculo en el plano.
Un meridiano ( círculo máximo de la esfera que pasa por los puntos N y S, y es perpendicular al ecuador) se reflejará como una circunferencia degenerada en una recta que pasa por el punto S, y cualquier círculo máximo en la esfera intermedio se reflejará como una elipse más o menos excéntrica.
Ahora sí lo podemos decir: una esfera menos un miserable punto es topológicamente equivalente a un plano.

También podemos hacer que la esfera y el plano sean equivalentes de otra forma: en vez de eliminar un punto de la esfera, añadimos un punto al plano. Parece una estupidez añadir un punto a un plano (¿Dónde lo ponemos?) Sin embargo, no lo es. Se puede definir perfectamente un "punto en el infinito" que será el reflejo (a estas alturas espero que lo hayan adivinado) del puñetero punto N de la esfera; el único que quedaba sin emparejar. Esta construcción se denomina compactificación del plano mediante la adición de un punto en el infinito.

El Poliedro de Szilassi (y 3)

Prosigamos según el esquema que nos hemos marcado en los dos post anteriores.
Vamos a investigar si puede existir un poliedro tridimensional con un agujero( topológicamente similar a una rosquilla o a un toro) que tenga la propiedad tetraedral consistente en que todo par de sus caras se encuentra en una arista.

Ahora el fórmula del ”Teorema de Euler” nos dice que

C – V + A = 2 – 2h

Como h es el número de agujeros, y ahora tenemos uno, la cosa queda así:

C – V + A = 0

Diremos que la característica de Poincaré de los poliedros con un agujero vale cero. Las otras dos ecuaciones que ligaban aristas , vértices y caras permanecen invariables, pues surgían naturalmente de la imposición de que cara par de caras compartieran una arista común.

Si introducimos aquellas dos ecuaciones, que eran:

A = C ( C – 1 ) / 2
V = 2 A / 3

Obtenemos:

C²-7C=0 , que es lo mismo que:
C ( C – 7 ) = 0

Que tiene dos soluciones; C=0 y C=7. La primera no nos interesa, porque con cero caras poco podemos hacer, y la segunda es la gran sorpresa:

Con siete caras, tenemos A=(7x6)/2=21 aristas y V=21x2/3=14 vértices. Así pues, parece existir un extraordinario poliedro con tan sólo siete caras, con 21 aristas y 14 vértices, que es topológicamente similar a una rosquilla por tener un agujero, y que además cada par de caras se encuentran en una arista. Podemos saber además que todas las caras son hexagonales, pues cada una de las siete debe tener una arusta común con las seis restantes. Sabemos también que de cada vértice salen exactamente tres aristas

Lajos Szilassi presentó en sociedad tal joya geométrica en el año 1.977: el heptaedro toroidal , o poliedro de Szilassi.



Tiene exactamente las propiedades que hemos predicho: tiene un agujero, siete caras hexagonales, 21 aristas y 14 vértices. Pueden admirarlo en la figura. Si alguien tiene el interés de construirlo, tiene también el desarrollo del mismo.

Espero que les parezca, como me parece a mi, maravilloso que podamos saber todas las características importantes de un objeto mucho antes de que sea descubierto. Con la única fuerza del razonamiento matemático.


¿Se acuerdan del teorema de los cuatro colores?
Cuatro colores bastan para colorear cualquier mapa sobre un plano o sobre una esfera de forma que dos países que comparten frontera común sean de distinto color.
El teorema era topológico, de forma que nada nos afirma del número de colores necesarios para un mapa sobre un toro, por ejemplo. ¿Qué relación tiene esto con el poliedro de Szilassi?
De ello hablaremos en el siguiente post.

El poliedro de Szilassi (2)

Centrémonos en nuestra pregunta: ¿puede existir algún poliedro, además del tetraedro (regular o no) tal que cualquier par de caras tenga una arista en común?

Sabemos que, si no tiene agujeros, debe cumplir la relación:

(1) C – A + V = 2

Además, podemos establecer una relación entre las caras y las aristas. Efectivamente, habrá tantas aristas como parejas de caras. Si tenemos C caras, tendremos C(C-1)/2 aristas.

¿Porqué? Pues muy sencillo: Dada una cara cualquiera, tiene (C-1) caras más con las que formar una arista, luego tendremos C(C-1)/2 posibilidades. Dividimos por 2 porque cada arista ha sido contada dos veces: cuando tomábamos una de las caras, y cuando tomábamos la otra. Dicho de otra forma: el número de aristas es igual al número de parejas de caras, que es la combinación de C elementos tomados de dos en dos.

Así pues, tenemos:

(2) A=C ( C – 1 ) / 2

Respecto a los vértices, ¿podemos decir algo? Pues sí, podemos: en un vértice deberán unirse exactamente tres aristas. Menos de tres es imposible si queremos tener un sólido con volumen; y si fueran cuatro o más, tendríamos dos caras que sólo comparten un vértice, y queremos que toda pareja de caras comparta una arista. También sabemos que una arista corresponde por definición a dos vértices, luego podríamos contar el número de aristas contando el número de vértices, multiplicándolo por tres y dividiendo entre dos.

Por lo tanto:

(3) A = 3 V / 2 => V = 2 A / 3

Tenemos tres ecuaciones contres incógnitas: sustituyendo la segunda y la tercera en la primera, obtenemos lo siguiente:

C² - 7C –12 =0

Que tiene dos soluciones: C=3 y C=4.

Con tres caras no tenemos poliedro alguno, y con cuatro tenemos lo que ya sabíamos: EL TETRAEDRO . Por lo tanto, no existen más poliedros, al menos sin agujeros, que cumplan la propiedad del tetradero.

Hemos demostrado un teorema de inexistencia, y eso es más fuerte de lo que en principio parece: no existe, ni existirá ni ha existido jamás un poliedro tridimensional sin agujeros con la propiedad de que toda pareja de caras se encuentra en una arista, salvo en tetraedro (regular o no, eso no importa ahora).

Debemos pues buscar entre objetos más exóticos: vayamos a los poliedros con un agujero; topológicamente equivalentes a un toro o una rosquilla.

Dentro de esa fauna encontraremos lo que queremos. Será en el siguiente post.

El poliedro de Szilassi (1)

Una de las posibilidades más increíbles de la matemática es que permite demostrar la existencia o inexistencia de objetos (incluso geométricos, que podamos construir o tallar en un trozo de madera) de los que poco sabemos: un puñado de propiedades tal vez, pero no su aspecto. Tengan presente que estoy hablando de existencia matemática, de forma platónica.

Esa posibilidad es tan potente que la matemática la exporta al resto de las disciplinas científicas. Cuando leemos que un científico postuló la existencia de una partícula años antes de que fuera descubierta, estamos asistiendo a este aspecto de la ciencia del que hoy les quiero hablar.

La matemática ocupa un estatus muy especial dentro de la ciencia: no estudia el mundo, sino los modelos abstractos que los científicos construyen para entender el mundo. Si los modelos son adecuados y la matemática subyacente a ellos postula la existencia de un determinado objeto, tiene mucho sentido buscarlo y encontrarlo.

Con la matemática pura, no aplicada, pasa algo parecido, si bien el símil no es completo: no nos referiremos a la existencia física de un objeto, sino a la existencia matemática. No partiremos de un modelo del mundo que quizás, después de todo, sea falso, sino que trabajaremos sin hipótesis adicional alguna. Y si conseguimos demostrar nuestra afirmación, así quedará hasta el fin de los tiempos.

Quiero invitarles a un paseo quizás un poco más empinado que en otras ocasiones, pero que intentaré hacerlo fácil. Me gustaría llegar con ustedes a la convicción de que existe un cuerpo tridimensional muy especial del que a priori nada sabemos, y hacerlo pasito a pasito. Nos adentraremos un poco en aspectos topológicos y geométricos en general.

En el fondo, si yo pudiera demostrar tales cosas por mí mismo, seguramente no estaría haciendo un blog, sino escribiendo en revistas especializadas, de manera que les confesaré desde el principio que hay una trampa: el objeto YA fue descubierto en 1.977.

Es un poliedro muy especial, como verán. Espero que el viaje les sea ligero, aunque quizás en algún momento requiera un poco de concentración. Para hacerlo más liviano, partiremos el asunto en varios post.

Comenzar por los llamados sólidos platónicos me parece lo más apropiado. Como sabrán, los poliedros regulares son aquellos cuerpos sólidos cuyas caras son polígonos regulares, todas ellas iguales. Existen cinco (ni uno más ni uno menos), que son: el tetraedro, el hexaedro o cubo, el octaedro, el dodecaedro y el icosaedro. Los pueden ver en la figura.

Cada uno de los cinco es una pequeña maravilla, que queda empequeñecida ante la magnificencia de la demostración de que estos son todos los poliedros regulares. Esta demostración es (según mi humilde entender) una de las más bonitas cosas que los matemáticos hayan realizado nunca. No en vano, el propio Carl Sagan no pudo resistirse, y en las últimas páginas de su best seller Cosmos incluyó la demostración . Hizo bien. Incluyó también la demostración de que la raíz cuadrada de dos es un número irracional, algo de importancia imposible de calibrar si uno no sabe previamente el horror que tal hecho causaba a los griegos, pero esa es otra historia.

La demostración que explica Sagan de que cinco son los sólidos platónicos, o regulares, se basa en una propiedad muy importante de todo poliedro, que los niños aprenden en los colegios con el nombre de Teorema de Euler , como si el bueno de Euler hubiera demostrado un único teorema en su vida.

Este teorema se expresa mediante la siguiente fórmula:

C – A + V = 2

Siendo C el número de caras, A el de aristas y V el de vértices. Lo que los niños no saben es que esto sólo es cierto para poliedros sin agujeros. Un prisma hexagonal con un agujero hexagonal en el centro por ejemplo no lo cumple. La fórmula generalizada para todo tipo de poliedros es:

C – A + V = 2 - 2h

donde h es el número de agujeros. Estamos en terrenos topológicos, donde lo que estudiamos son las propiedades más escondidas de los cuerpos geométricos: aquellas que permanecen invariantes por mucho que los deformemos mientras la demormación sea continua. El número entero C – A + V se llama característica de Poincaré de dicho cuerpo, por buenos motivos que veremos en su día.

Llevo cierto tiempo queriendo hablar de esta fórmula, engañosamente simple y de los secretos que encierra, pero lo dejaremos para mejor ocasión, y si les parece la daremos por buena. Cuando un cuerpo no está formado por caras planas, podemos hacer mediante deformaciones contínuas que sí lo sean, por lo que podemos hablar de su característica de Poincaré del mismo modo. Así, una esfera podemos convertirla en un cubo a martillazos, por lo que su característica de Poincaré será igual a 2, igual que cualquier sólido platónico.

De entre los cinco sólidos platónicos, sólo uno cumple la propiedad de que dado un par de caras, tienen frontera común: una arista. Para los otros cuatro, siempre podemos encontrar dos caras que no se toquen, y por lo tanto no compartan ninguna arista.

Nuestra pregunta es doble: ¿existen más poliedros (regulares o no) que exhiban esta propiedad del tetraedro? ¿Caso de existir, qué podemos saber de ellos?

La reflexión sobre esta pregunta nos llevará bastante lejos, y descubriremos que la respuesta es positiva, y que aún sin saber cómo demonios pueden ser dichos cuerpos, podemos afirmar de una forma aparentemente mágica pero perfectamente rigurosa muchas de sus propiedades.

Posteriormente, presentaremos tal cuerpo: el poliedro de Szilassi . Espero que el asunto tenga el suficiente misterio como para que me quieran acompañar en este paseo.

Independencia ( y 2)

En el post anterior no hay trampa alguna. Las variables aleatorias X₁ y X₂, que indicaban el sexo del primer y del segundo hijo son realmente independientes. El sexo de cualquiera de ellos no influye para nada en el sexo del otro. Lo que ocurre es que cuando decimos que “al menos uno de ambos es chica” erróneamente pensamos que estamos hablando de alguna de estas dos variables aleatorias independientes, y eso no es así. Comprender esto es básico para entender lo que sigue.

Vamos a verlo pausadamente. Definimos una variable aleatoria nueva, que llamaremos Y definida así:

Y= X₁+ X₂

Los valores de Y que podemos encontrar en nuestro matrimonio son 0,1 y 2. (Recordemos que cualquiera de las X valía 0 si el correspondiente hijo era varón y 1 si era hembra. Y no es más que el número de hembras que tiene la pareja.

El suceso {alguno de los hijos es chica} es exactamente el suceso {Y es mayor o igual que 1}. El suceso {la otra también es chica} es exactamente el suceso {Y=2}.Tan sólo ver la definición de Y , y comprobar que las dos variables X están presentes en dicha definición, vemos claro que no es independiente de las mismas. Repetimos una vez más: las variables X₁ y X₂ son independientes entre sí, pero la Y depende de ambas.

Cuando tenemos un conocimiento parcial de qué es lo que ocurre, como en nuestro caso (sabemos que al menos una es chica), las probabilidades se reajustan a dicho conocimiento, siempre que el suceso estudiado no sea independiente de esa nueva información. Hablaremos entonces de probabilidades condicionadas, porque están condicionadas a un conocimiento parcial que poseemos, o que suponemos conocido. Lo expresamos matemáticamente mediante una barra vertical que por misterios informáticos no puedo poner aquí, de forma que usaré la barra(/), que no deberemos confundir con una división.

Diremos entonces:

P( x₁/ x₂)= P( x₁)
P( x₂ / x₁)= P( x₂)


¿Qué quiere decir esto? Pues muy sencillo: las probabilidades de x₂ conocidos los valores de x₁ son las mismas que sin tener en cuenta a x₁ para nada. Eso ya lo sabíamos: que el primer hijo sea chico o chica no condiciona para nada el sexo del segundo.

Diremos que dos variables aleatorias A y B son independientes si y solo si

P(A/B)=P(A)
P(B/A)=P(B)

¿Y en nuestro problema, qué es lo que ocurre? Pues ocurre que nos estamos preguntando por la probabilidad del suceso {Y=2} condicionado a que ocurre el suceso {Y es mayor o igual que 1}. Nadie podría esperar independencia de una variable respecto a un conocimiento parcial de la misma variable, ¿verdad?

Veamos cómo afecta este conocimiento:

Los valores posibles de Y (número de chicas) era 0,1, ó 2, con las siguientes probabilidades:

P(Y=0) = 0.25 (una posibilidad entre cuatro: primer hijo chico y segundo también)
P(Y=1) = 0.5 (dos posibilidades entre cuatro: primer hijo chico y segundo chica y viceversa)
P(Y=2) = 0.25 (una posibilidad entre cuatro: primer hijo chica y segundo también).

Al saber que una al menos es chica, sabemos que Y no puede valer cero, luego la probablidad total se debe redistribuir entre los dos sucesos restantes, {Y=1} y {Y=2}. Antes de dicho conocimiento, estos dos sucesos sumaban el 75% de la probabilidad total, ahora suman el 100%, pues hemos descartado la posibilidad {Y=0}. Técnicamente diremos que el conocimiento parcial del asunto nos ha disminuido el espacio muestral, y debemos reasignar probabilidades a los sucesos.

Si la suma que antes era el 75%, ahora se ha ampliado hasta el 100%, por una simple regla de tres podemos comprobar que las probabilidades para los sucesos {Y=1} y {Y=2} quedan del 66,66% y del 33,33% respectivamente.

Volvemos a obtener que es el doble de probable que el otro hermano sea chico (suceso {Y=1}) que chica (suceso {Y=2})si sabemos que uno de ellos al menos es chica. Como sabíamos por el post anterior.

Ya ven, al final todo se entiende (¡espero!), pero para nosotros los humanos es mucho más fácil reconocer incluso por teléfono la voz de un amigo que no hemos oído hace años que estimar intuitivamente de forma correcta las probabilidades de un suceso tan simple como éste. Sin embargo, la correcta estimación de probabilidades, como decía en el post anterior, tiene evidentes ventajas para la supervivencia. ¿Porqué no hemos sido mejor dotados para ello?
No tengo ni idea.

Independencia

Es una desgracia que tenemos los humanos: nos es muy difícil estimar probabilidades. Somos capaces de habilidades casi milagrosas, que compartimos con el resto de los mamíferos en mayor o menor grado: podemos “calcular” la velocidad y dirección en la que debe salir un proyectil de nuestra mano para alcanzar un blanco móvil, cuestión no sólo no trivial, sino muy complicada. Y lo hacemos instintivamente. Podemos reconocer los tonos de voz de múltiples personas, para lo cual hemos tenido que realizar previamente un análisis de Fourier complicadísimo de las ondas sonoras, extrayendo la información relevante no sólo del contenido de los mensajes, sino de las características propias que nos hacen identificar cada voz con su dueño. Esto es una proeza casi inconcebible, y la realizamos sin esfuerzo alguno.

Sin embargo, por alguna razón la evolución no nos ha dotado de la capacidad para estimar probabilidades de forma automática, y debemos recurrir al esfuerzo, la concentración en el problema y la metodología matemática. Sin duda es una pena: el tema no es en absoluto baladí, sino que presenta una interés evidente con enorme implicación en la vida real.

La teoría de la probabilidad hunde sus cimientos en la teoría de la medida, que es el estudio de unas funciones de conjunto con unas determinadas buenas propiedades, pero es mucho más que teoría de la medida. Uno de los conceptos que la enriquecen es el de independencia, concepto ausente en teoría de la medida.

Para andar por casa, diremos que una variable aleatoria es la materialización numérica de un suceso debido al azar. Por ejemplo: el número de puntos conseguidos al lanzar un dado, el número de hijos de cualquier pareja, el número de coches de color verde que me cruzo cada vez que vuelvo a casa desde el trabajo.

Dos variables aleatorias son independientes cuando la realización de una no influye en la de la otra. En dicho caso, las probabilidades se pueden multilicar sin ningún problema. Si la probabilidad de un suceso es p y la de otro indepeniente es q, la probabilidad de que se den los dos es pq.

Vamos a proponer un ejemplo enormemente sencillo para ver lo que nos cuesta estimar probabilidades:

En un matrimonio con dos hijos, si uno de ellos es chica, ¿qué probabilidad hay de que el otro también sea chica?

Es un buen ejemplo de dos sucesos independientes: el sexo de uno de los hijos no influye para nada en el sexo del otro. En un razonamiento ingenuo diríamos que no hay duda: el otro puede ser tanto chico como chica con igual probabilidad, luego la respuesta es el 50%.

Veámoslo un poco más en profundidad.

Sea X₁ el sexo del primer hijo, y X₂ el del segundo, que daremos arbitrariamente el valor de 0 para varón y 1 para hembra. Las probabilidades de ocurrencia de ambas variables aleatorias son:

P(X₁=0)=P(X₁=1)=0,5
P(X₂=0)=P(X₂=1)=0,5

Como ambos sucesos son independientes, tenemos que las probabilidades de ambos sucesos se pueden multiplicar, obteniendo:


P(X₁=0,X₂=0)=P(X₁=0,X₂=1)=P(X₂=1,X₂=0)=P(X₂=1,X₂=1)=0,25


Tenemos cuatro posibilidades equiprobables: chico-chico (0,0); chico-chica (0,1),chica-chico(1,0) y chica-chica(1,1); cada una con una probabilidad del 25%.

Hasta aquí ningún problema, ¿verdad?

Ahora el enunciado del problema nos indica que de las cuatro posibilidades a priori, sólo tenemos tres, dado que al menos una hembra hay.

Podemos tener chico-chica, chica-chico y chica-chica, con igual probabilidad. Tres posibilidades, de las cuales sólo una cumple que la otra también es chica, luego la probabilidad pedida es 1/3, o el 33,33%.

Hemos demostrado que en un matrimonio con dos hijos en el que al menos uno de los cuales es chica, es el doble de probable que el otro sea chico (2/3 frente a 1/3). Dada la simetría de sexos, podemos generalizar:

Si sabemos que al menos uno de los dos hermanos es de un sexo dado, es el doble de probable que el otro sea de sexo contrario .

¿Cómo es posible que ocurra esto, y que sigamos defendiendo que el sexo del primero y del segundo son independientes?

La comprensión de este asunto es de importancia capital para entender la independencia entre variables aleatorias, y queda pendiente para otro post. Como siempre, si ustedes quieren.

Biyección entre un minúsculo segmento y el universo.

En cierto modo, vamos a cerrar un ciclo.

Hemos visto y demostrado que el conjunto de los números racionales es numerable.
Hemos visto y demostrado que el conjunto de los números reales o de los puntos de la recta no lo es.
También hemos dicho que la potencia de R es tal que cualquier segmento, por pequeño que sea tiene tantos puntos como el universo entero. Pero no lo hemos demostrado.

Dado que algún lector me ha manifestado estar de acuerdo conmigo en que lo importante no es sólo el resultado, sino también el camino, y dado que la demostración de esta increíble afirmación está al alcance de cualquiera, paso a exponerla. Como siempre en estos casos, se debe a Cantor, y consta de dos pasos: demostraremos primero que existen tantos puntos en un segmento cualquiera como en toda la recta, y veremos luego que existen tantos en una recta como en un plano. La extrapolación del plano al espacio tridimensional, tetradimensional o n-dimensional es inmediata, como veréis, siempre que n sea finito.

El fabuloso método de correspondencia que veíamos en el post anterior no se puede aplicar tan sólo en los conjuntos finitos, sino que vale también a los infinitos, como sabéis si me habéis leído. Ocurren entonces cosas extrañas, como que un conjunto es comparable a una parte suya. La extrañeza que esto nos produce se debe a que en nuestra vida cotidiana manejamos objetos finitos, en los que la parte es inferior al todo, pero sirve de hecho para definir a los conjuntos infinitos como aquellos que son de la misma potencia que alguna de sus partes. No nos preocuparemos por ello.



En la primera foto podéis ver el método que usó Cantor para crear una biyección entre los puntos de un segmento AB cualquiera y toda una recta. Basta mirar el dibujo para convencerse sin necesidad de mayor explicación que podemos encontrar para cada punto x del segmento un f(x) de la recta, y viceversa, luego ambos tienen el mismo número de elementos: aleph_uno.



En la segundo foto veis la forma de biyectar el segmento [0,1] con el cuadrado de lado unidad. Dado que todo real entre cero y uno es de la forma 0,x₁x₂x₃x₄,... podemos “fabricar” dos reales, uno con los decimales en puesto par y otro con los decimales en puesto impar, que serían las coordenadas X e Y del punto f(x) del cuadrado que le corresponde a nuestro x original. Viceversa, cada un punto del cuadrado tiene dos coordenadas; intercalando los decimales de ambas podemos obtener un único número real que pertenezca al segmento.
Ambas operaciones son unívocas e inversibles, luego la biyección está demostrada.

Pasar del cuadrado unidad a todo el plano es tarea bien sencilla, e incluso a un espacio de cualquier número finito de dimensiones: en el espacio tridimensional tenemos tres coordenadas para cada punto: intercalaríamos los decimales de tres en tres: primero el de la coordenada X, luego el de la Y, luego el de la Z, y el siguiente sería el correspondiente de la X otra vez...
Podemos comprobar que dos simples gráficas nos explican por sí solas la veracidad de una proposición que en principio es absolutamente increíble. En algún momento afirmé que no me parece cierto que una imagen vale siempre más que mil palabras; pero si la imagen está bien elegida puede ciertamente en algunos casos valer más que cualquier explicación...

CARACTERIZACIONES

Hemos comentado varias veces que la palabra “elemental” en matemáticas es un arma de doble filo. Las demostraciones elementales de teoremas en teoría de números, por ejemplo son el paradigma de la extrema dificultad, mientras que utilizando el arsenal sofisticado del análisis complejo, las demostraciones muchas veces se realizan en dos renglones. Así mismo hay conceptos elementales que son difíciles de aprehender, y tan sólo son elementales porque no surgen de generalizar otros conceptos preexistentes.

No va a ser así en este caso: vamos a hablar de algo fundamental en la matemática, algo elemental y a la vez muy sencillo. Se trata de las condiciones suficientes, las condiciones necesarias y las condiciones suficientes y necesarias (caracterizaciones). Estos sencillos conceptos impregnan la matemática toda, y nada es posible hacer sin ellos. Dado que en los últimos post hemos estado hablando de los números racionales, vamos a servirnos de ellos para hablar de estos conceptos.

La definición formal de lo que es un número racional es un poco más complicada de la que vamos a ver aquí, porque implica el manejo de clases de equivalencia (otro de los conceptos capitales en matemáticas), pero daremos por buena la siguiente definición: “ Un número racional es un número expresable por el cociente de dos enteros”.

Un número de este tipo tiene una expresión decimal formada por una parte entera, una coma y una serie infinita de decimales. Digo infinita, porque considero que para aquellos racionales que “sólo tienen cierto número de decimales”, existe una secuencia infinita de ceros tras ellos.

Los números reales irracionales también son expresables de la misma manera. ¿Son diferentes unos de otros en su expresión decimal?

Lo son. Esta diferencia desgraciadamente no siempre sirve para saber si un número es racional o no, por causas que luego veremos y que ahora no importan. Lo importante ahora es que esa diferencia existe, y sirve EN PRINCIPIO para diferenciarlos.

Vamos a demostrar los siguiente: Si un número es racional, entonces a partir de un momento, sus decimales se repiten periódicamente. Basta ver el algoritmo usual de la división (ver figura):
Cada nuevo decimal que hallamos se obtiene operando con el resto que nos queda del anterior, ¿verdad? Dado que el resto debe ser un entero menor que el divisor, sólo existen un número finito de restos posibles distintos. Eso quiere decir que antes o después nos encontraremos con un resto que ya teníamos, y a partir de ese momento, todo se volverá a repetir irremisiblemente.

¿Hemos demostrado ya la diferencia entre los racionales e irracionales? En absoluto. Lo único que hemos demostrado es que > Si un número es racional, entonces a partir de un momento, sus decimales se repiten periódicamente. Nada sabemos de momento al respecto de la posibilidad de periodicidad en los decimales de los irracionales. Lo que tenemos es una condición necesaria para tener un racional. ¿Porqué necesaria? Pues muy sencillo, porque al demostrar que todo racional cumple la periodicidad en sus decimales, sabemos automáticamente que todo incumplimiento de esta circunstancia implica que el número no es racional. Es necesario que se cumpla la condición para tener un racional. Aún no sabemos si es suficiente.

Demostremos ahora lo siguiente: Si a partir de un momento, los decimales de un número se repiten periódicamente, entonces el número es racional.

Esto es también muy fácil. La parte periódica del número (que tendrá, n cifras, puede expresarse como el cociente de dichas cifras entre el número formado por tantos nueves como cifras tiene, por ejemplo 0.123123123123123...= 123/999 , luego es racional. Si dicha parte empieza en el n-ésimo decimal, basta añadir (n-1) ceros en el denominador: 0.0000123123123123123...= 123/9990000.
La parte que queda del número (sus primeros decimales hasta llegar a la parte periódica) siempre será racional, pues bastará dividir sus cifras por la potencia de 10 necesaria.

( 0,765123123123123...= 0,765+0.000123123123...=( 765/1000 )+ ( 123/999000) )

Y como la suma de dos racionales es siempre otro racional, ya está demostrado.

Esta última demostración es inversa a la anterior: ahora sabemos que si hay periodicidad, entonces el número es racional; antes sabíamos que si el número era racional, había periodicidad. Antes teníamos una condición necesaria para la racionalidad , ahora tenemos una condición suficiente.

Dado que en ambos casos la condición es la misma, tenemos una condición suficiente y necesaria , que en matemáticas es lo más guay que se puede tener. ¿Porqué? Pues porque si se cumple la condición, estamos con un racional, y si no se cumple, no. Este tipo de condiciones resume la esencia del problema completamente. Tanto es así, que a partir de ese momento, podemos sustituir la definición primitiva que teníamos, por el cumplimiento de la condición sin ningún problema. Eso es una caracterización.

Siempre que encontréis una frase matemática en la que figure la coletilla si y solo si , estaréis ante una caracterización, que sustituye a una definición. Será siempre una condición suficiente y necesaria para que se cumpla algo, y recogerá en una frase la esencia del problema. Concisión y economía de pensamiento: parte importante de la belleza matemática, ¿no creen ustedes?

La insoportable levedad del conjunto Q (y 2)

Prometimos demostrar que el conjunto de todos los números reales no era numerable, que es lo mismo que decir que no se podían poner en relación biunívoca con los enteros positivos. Otra forma de decirlo es que no podemos hacer un listado en el que figuren todos ellos.

Un comentario antes de seguir: tampoco podemos hacer un listado en el que entren todos los enteros naturales, porque son infinitos, pero eso no debe importarnos: se trata de la posibilidad o imposibilidad de idear un procedimiento para listar todos los elementos de un conjunto infinito sin dejarnos ninguno. Dado que son infinitos, la materialización práctica de este procedimiento nunca podríamos realizarla, pero (y esto es lo importante) si tenemos un método de hacerlo, siempre podríamos, ante cualquier elemento del conjunto, preguntarnos qué puesto ocupa en la lista. Eso es lo importante. Por eso decimos que el conjunto de los naturales es numerable, porque lo podemos numerar, no porque podamos exhibir un listado completo de todos ellos. Ante la pregunta de qué puesto ocupa el entero positivo n, la respuesta obvia es: ¡el n-ésimo puesto ! Misión cumplida. Eso es lo que demostraremos imposible para los reales.

La demostración, ¡cómo no!, se debe a Cantor, el hombre que amaba las diagonales. Es absolutamente demoledora en su simplicidad, y demuestra por reducción al absurdo que no se puede, ni en principio, idear un método para realizar una lista de todos los números reales comprendidos entre cero y uno. Por ende, más imposible será tener la de todos los reales.

Supongamos que sí se puede realizar tal listado exhaustivo; cada número real entre 0 y 1 tiene una expresión decimal que empieza por cero coma ..., por ejemplo 0,363527682329... los decimales son evidentemente infinitos, aunque a partir de un momento puedan ser todos iguales o todos cero (como sucede con algunos racionales, que no por serlo dejan de ser reales). Tenemos de esta forma, aceptando la posibilidad de tal procedimiento, un listado infinito en el que están todos los números reales. Vamos a construir un número real comprendido entre cero y uno ayudados por la lista anterior de la siguiente forma (ver imagen): empezamos con cero coma (0, ) para el primer decimal, nos fijamos en el primer decimal del primer número de la lista. Si es un número distinto de cero, ponemos un cero y si es un cero, ponemos un uno. Seguimos de forma idéntica: para el segundo decimal, nos fijamos en el segundo decimal del segundo número de la lista. Si es un número distinto de cero, ponemos un cero y si es un cero, ponemos un uno. Y así por siempre jamás. Los únicos guarismos en los que nos fijamos son los de la diagonal coloreada de la imagen.

Lo interesante del asunto es que hemos construido un número real entre cero y uno que tiene su primer decimal distinto que el primer decimal del primer número de la lista... su n-ésimo decimal distinto del n-ésimo decimal del n-ésimo número de la lista, etc,etc... Es decir: hemos construido un número real diferente a todos los de la lista , lo cual debiera ser imposible, pues hemos partido de la hipótesis de que teníamos una lista infinita pero completa de todos los reales entre cero y uno. Así pues, la hipótesis de partida es la que era falsa: nunca podremos tener tal lista.

Dado que los reales son los racionales más los irracionales, y hemos demostrado en el post anterior que los racionales son numerables, los responsables de la no numerabilidad de R tienen que ser los irracionales, esos mismos que en el post anterior los veíamos ingenuamente en pie de igualdad al fijarnos en la densidad de los mismos en R. La realidad es mucho más compleja: casi todos los reales son irracionales, y eso es compatible con el hecho de que en cualquier entorno abierto de R , por pequeño que sea nos encontramos infinitos racionales e irracionales.

Hay algo muy misterioso en todo esto: hemos demostrado que no puede haber un listado completo de todos los reales comprendidos entre cero y uno. Y lo hemos hecho dando un método constructivo para expresar un número real que necesariamente no puede estar en el listado de partida, que suponíamos completo. Me van a permitir una pregunta. ¿Porqué no podemos hacer exactamente lo mismo con el conjunto Q?, A partir de un presunto listado exhaustivo de todos los racionales, construir uno nuevo que sea diferente a todos ellos en al menos un decimal. Habríamos demostrado que Q tampoco es numerable, a pesar de que conocemos otra demostración de que sí lo es (la del post anterior).¿Qué es lo que está fallando aquí? ¿Les apetece pensarlo un poquito?

Les espero...

La insoportable levedad del conjunto Q

Para Reyes, mi
paseo más hermoso

No estará de más recordar una vez más que esto es un paseo, y que no vamos a descubrir en este blog nada nuevo. Tratamos únicamente de visitar parajes hermosos, y de hacer un viaje compartido por el mundo de las ideas matemáticas. Digo esto porque muchos aspectos matemáticos, no por ser perfectamente establecidos y aclarados dejar nunca de tener su encanto.

El conjunto Q es el de los números racionales, o sea: los que se obtienen dividiendo dos enteros, positivos o negativos. Por ejemplo: 0,25 es racional por ser el cociente de 1 y de 4.

Aquellos números que no se pueden expresar mediante este sistema, son llamados en un alarde de imaginación irracionales . Tanto unos como otros son números reales, y estos últimos pueden ponerse en relación uno a uno con los puntos de una recta.

Uno de los primeros hechos interesantes es que todo irracional (pi, por ejemplo) puede ser aproximado mediante una división de enteros, tanto como se quiera; aunque nunca se obtenga dicho número exactamente. Por ejemplo 22/7 es una muy buena aproximación a pi, pues nos da su valor con un error relativo de tan sólo 0.04%. A base de numeradores y denominadores más grandes ( y menos elegantes), conseguiríamos precisiones cada vez mayores. Estamos descubriendo una característica importante del conjunto Q: es denso dentro de R.

La noción de conjunto denso es topológica, y necesita de conceptos previos (adherencia de un conjunto), pero existe una caracterización que nos viene muy bien. Un subconjunto D de un conjunto C es denso si y solo si todo abierto de C contiene algún elemento de D . En la recta real R los abiertos son los intervalos (a,b), que comprende todos los números reales mayores que a y menores que b, así como uniones de intervalos de este tipo, e intersecciones finitas de ellos.

Tomemos el punto origen (cero) de la recta. Imaginamos un entorno abierto centrado en el cero, infinitamente pequeño, pongamos de una billonésima (10 ^-12) de radio. Es muy fácil encontrar números racionales en el interior de este intervalo abierto, como puede verse en la figura.



Vemos que por muy pequeño que sea el intervalo, existen infinitos racionales dentro de él: en la figura hemos dibujado dos: los correspondientes a una décima y a nueve décimas de billonésima. Eso es lo que quiere decir que Q es denso en R .

Podemos percibir que el conjunto Q “invade” todo rincón del total R. De la misma forma, dado cualquier intervalo de R, sería igual de fácil encontrar irracionales en su interior, también en número infinito. Los irracionales invaden igualmente R. Adermás, ambos conjuntos, el Qde los racionales y el de los irracionales son disjuntos (un número o es racional y pertenece a Q, o no lo es, y pertenece al conjunto de los irracionales) y su unión hace todo R. ¿Puede darse mayor situación de empate?

Pues sí que puede, dado que ¡el empate es ficticio! De hecho, no hay empate en absoluto. A pesar de ser cierto que podemos aproximarnos cuanto queramos a cualquier irracional por medio de racionales, y viceversa, a pesar de que unos y otros están imbricados en la estructura de R a cualquier escala, por muy microscópica que la imaginemos, resulta que ambos conjuntos son muy diferentes, hasta el punto de que todo el peso de R se lo lleva el complementario de Q( el conjunto de los irracionales), no quedando NADA para Q, que como dijimos en otro post, no es sino humo fractal dentro de R.

Veamos esto con más detenimiento, porque aquí tenemos dos sorpresas:

1.- Dado que entre dos números reales cualesquiera, por muy cercanos que estén, existen infinitos racionales, parecería que no fuera comparable el número de racionales y el de naturales. No es así, pues ambos conjuntos tienen el mismo número de elementos.

2.- El tamaño o potencia de los racionales e irracionales aparenta ser igual, vista la “situación de empate” vista más arriba. Esto tampoco es así; la potencia de los irracionales es sipuerior a la de los racionales, como se ha dicho.

Para zanjar la sorpresa 1, Cantor demostró con su método diagonal que los racionales son numerables Esto significa que se pueden poner en orden sin saltarse ninguno, de forma 1º, 2º, 3º, ...si lo conseguimos, como cada racional se corresponde con un natural (entero positivo) y viceversa, entonces los tamaños de los dos conjuntos son iguales. La demostración es una tontería... salvo por el hecho de que a nadie se le ocurrió antes. Consiste en colocar todas las fracciones posibles en una tabla rectangular, eliminar las fracciones que representan el valor de una ya considerada, y recorrer la tabla en diagonal, como se indica en la figura. De esta forma no nos dejamos ninguna fracción por numerar, y cada entero se corresponde con una y solo una fracción. Queda demostrado para toda la eternidad que hay tantas fracciones como enteros positivos.

Dejaremos para el siguiente post la increíble demostración de que a diferencia de Q , R no es numerable. Entonces podremos apreciar la insoportable levedad de Q, en contra de toda apariencia. Os espero.

Atando cabos complejos

El post sobre el teorema de Lucas tendrá que esperar. Lo cierto es que hay algo que merece un apunte adicional a lo dicho anteriormente al respecto de la complejidad algorítmica. Tenemos la idea de que la cantidad de información, que medimos en bits, refleja de alguna manera el interés de aquello que consume esos bits: un mensaje de 1 mega tiene más información que un mensaje de 12 kB. Por otra parte, sabemos por experiencia que la longitud de un mensaje nada tiene que ver con su interés...

El concepto de complejidad algorítmica, aunque parece más traído por los pelos, es mucho más natural. Vamos por fases, y comienzo con una anécdota.

PRIMERA FASE

Cuando visité Florencia hace años, me planté bajo El David de Miguel Angel, y me asaltaron tres pensamientos. Dos de ellos nada tienen que ver con lo que se trata aquí; eran:

1.- La estremecedora belleza de la escultura.
2.- ¿Si ese era David, cómo sería Goliat?
La tercera sí tiene que ver con lo que aquí debatimos:
3.- El David “estaba” en el interior del bloque de mármol antes de que el escultor se limitara a quitar lo que sobraba.

Pensemos en la tercera cuestión. La escultura en piedra es una especie de arte inversa, se quita lo que sobra y queda... el resto; que es la obra de arte.

SEGUNDA FASE

Acabo de leer en un número del Investigación y Ciencia, esa maravillosa y sorprendente revista que un día habla de ciencia y otro de agua imantada una historia muy curiosa. Adaptada al caso sería así:

Diseñamos un programa de ordenador que cree todos los textos posibles de n páginas, con n grande. El primer texto tendrá todos los caracteres en blanco y el último todo zetas. Suponemos ilimitada capacidad de cálculo: velocidad de proceso infinita y almacenamiento de datos suficiente. El programa es muy tonto y simple; apenas unos renglones de código. Sin embargo genera todas las joyas literarias, escritas y por escribir de la historia de la humanidad, (además de mucha basura, cierto es).

TERCERA FASE: REFLEXION

Tenemos un paralelismo entre el bloque de mármol y el conjunto de archivos generados por el programa. Si yo quiero leer el quijote, no tengo más que encontrarlo entre los innumerables pero finitos archivos generados por el programa arriba explicado. Dado que tengo ordenados los archivos lexicográficamente, no tengo más que teclear E , y quedarán eliminados todos los libros que no empiezan por E , sigo con n , luego un espacio en blanco, luego u ,y despues n , otro espacio en blanco y sigo con l , u , g, a r... como el escultor, voy eliminando cada vez parte de los volúmenes que no me interesan. En definitiva: direccionar el archivo que me interesa implica reescribir el quijote, de la misma forma que quitar lo que sobraba era precisamente la genial obra de arte que Miguel Angel creó. El bloque homogéneo no portaba información sustancial, el conjunto de todos los volúmenes tampoco, a pesar de su ingente tamaño. Pero el volumen del Quijote sí porta mucha información sustancial a pesar de ser un subconjunto ínfimo del total de archivos generados. El David es una obra cumbre del arte humano, y el bloque inicial no lo era.

CUARTA FASE: CONCLUSION

La complejidad algorítmica de un conjunto puede ser infinitamente menor que la de un subconjunto suyo. Así expresado parece sorprendente, pero eso sólo es porque tenemos prejuicios: estamos demasiado acostumbrados a manejar teoremas de conservación, y funciones aditivas. A veces la parte es muy superior al todo; a veces el tamaño no importa (JAJAJAJA).

Ahora vemos que el concepto de complejidad algorítmica es más natural de lo que parecía a primera vista. Todos sabemos que diez minutos de radio con Javier Armentia o con Félix Arestienen mucha mayor complejidad algorítmica, y son mucho más interesantes que dos horas de sesión en el congreso. Por eso digo que esto no es más que un paseo, porque aquí no vamos a descubrir nada que no estuviera inventado...

Dios es un ludópata (y 2)

Continuamos con lo prometido en el post anterior. Decíamos ayer que la omega de Chaitin (Chaitin es el de la foto)pertenecía a una clase de números reales verdaderamente “malvados”. Veamos porqué es esto así.

Una de las características más importantes de este número es que es algorítmicamente aleatorio. Esto es decir bastante más de lo que parece a simple vista. Supone que no puede comprimirse en un programa más breve que él mismo. En otro post hablábamos de la aleatoriedad de pi, y de los posibles (seguros, más bien) mensajes en su interior. Decíamos allí que dado que en pi existía todo, incluso la codificación en bantú de “Lo que el viento se llevó”, en realidad no existía casi nada. No hay información, ni sustancia especial. Y explicábamos que Kolmogorov había ideado el concepto de complejidad (cantidad de información) de un objeto como el número de bits del programa más conciso capaz de generarlo. Existen programas muy cortitos que generan pi con sus infinitos decimales, luego la complejidad interior de pi es pequeña; no es algorítmicamente aleatorio. El conjunto de Mandelbrot, con sus recovecos infinitos y volutas bellísimas es generable también por programas muy cortitos, por lo tanto posee muy poca complejidad en el sentido de Kolmogorov.

Chaitin definió un objeto es algorítmicamente aleatorio como aquel imposible de generar por un programa más corto que sí mismo en la década de los 60 del siglo pasado, prácticamente a la vez que Kolmogorov. Demostró que todo número algorítmicamente aleatorio era normal (sus dígitos aparecían con igual frecuencia en el desarrollo decimal, y en cualquier base). Decididamente, este tipo de números es bastante “peor” que un trascendente como pi.

El trabajo de Chaitin es muy técnico, y tedioso. De hecho, si repasan la definición de omega, verán que la suma de las probabilidades extendida a todo n no tiene ni porqué ser convergente, se hacía necesaria una normalización para que el propio omega fuera una probabilidad, comprendida entre 0 y 1. Este “detalle” le costó diez años de trabajo. Vemos por tanto que desde aquí no podemos sino hacernos eco de las propias declaraciones del autor referentes al asunto. Esto no es más que un paseo, recuerden...

A pesar de que este número está perfectamente definido y acotado entre cero y uno, en palabras de Chaitin, referidas a la expansión decimal binaria de omega:

“No solamente no se puede calcular este número, sino que nunca se pueden saber cuáles son sus bits, porque esa información es matemáticamente incompresible... es incompresible e incomprensible; las palabras son muy semejantes.”
“Para obtener los n primeros bits de omega necesito una teoria de n bits, de complejidad igual al fenómeno que quiero estudiar. Eso significa que no gano nada razonando.”

Nuestro omega no tiene estructura: es puro azar a pesar de estar perfectamente definido.

Queda claro que nuestro diablo encierra muchos secretos, y digo bien al decir “encierra”: nunca los desenterraremos. La única forma de seguir a delante es incorporar como axiomas los sucesivos valores de los bits de omega, pero incorporando axiomas, podemos demostrar cualquier cosa...

No obstante, el trabajo de Chaitin es bastante más preocupante de lo explicado hasta aquí. En matemáticas es posible trasladar la formulación de un problema a otro ámbito, si se es capaz de demostrar que existe un isomorfismo que posibilita tal traslado. En teoría de la complejidad es práctica habitual hacerlo, reformulando problemas complejos en términos de otros problemas complejos.

Chaitin consiguió traducir el problema del enésimo bit de omega en una ecuación diofántica (de coeficientes enteros). que ocupaba 200 páginas, tenía 20.000 variables y un parámetro. Demostró que ambos problemas eran isomorfos, y que la pregunta ¿Es cero o uno el enésimo bit de la expansión decimal binaria de omega? en el primer problema correspondía a la pregunta ¿Tiene un número finito de soluciones la ecuación cuando hago el parámetro igual a n?

Entiendan bien esto, que es importante: Tenemos dos problemas, A y B que se han demostrado isomorfos. Tenemos la demostración de que el problema A es no computable, algorítmicamente aleatorio, caótico e irresoluble. Para nada ayuda el planteamiento B a encontrar solución en el A; pero hemos demostrado que B es igualmente aleatorio, y ESO es lo terrible. El azar está incrustado en el seno mismo de la aritmética, dominio de las ecuaciones diofánticas.

Todo esto viene a ser una tercera formulación de la maldición de Gödel. La pregunta la hizo Hilbert, la contestó Gödel , la replanteó Turing y ahora la vuelve a responder Chaitin.

Aquí teneis una página personal de Chaitin con acceso a sus documentos más importantes, de los que he sacado esta información.

Y aquí teneis una entrevista en castellano a Chaitin en la que se habla del número omega.

PD. Por cierto, revisando documentación para este post me he encontrado con que Chaitin utilizó el Teorema de Lucas para desarrollar su ecuación diofántica. Este bonito teorema habla de la paridad los coeficientes del triángulo de Tartaglia. Sobre este tema será el próximo post, por poner algo fresquito y alegre :)

Dios es un ludópata (1)

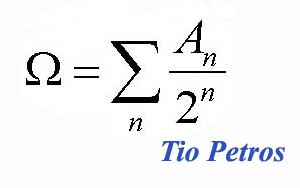A Einstein no le habría gustado este post. Uno de los padres de la mecánica cuántica renegaba de la criatura con la frase “Dios no juega a los dados”.

Churchil era un buen creador de frases de complejidad irreductible: pensamiento condensado en pocas palabras, y nuestro bienamado Albert no le iba a la zaga. A Einstein no le gustaba el azar, y creía en la existencia de variables ocultas, que es otra forma de decir que lo que parece azar no es sino falta de información por nuestra parte.

En el fondo, me parece a mi que la cuestión es muy poco científica: nos gusta o no nos gusta que el azar y el caos esté formando parte de la substancia misma de las cosas en función de nuestras apetencias, criterios, opiniones e ideología. Pero una de las pocas propiedades del universo de la que podamos estar seguros es la nula atención que presta a nuestros gustos particulares.

En una visión superficial del asunto, alguien podría decir que la matemática acepta desde siempre el azar; al fin y al cabo tenemos la teoría de probabilidades aceptada y bien establecida desde hace mucho tiempo. Pero la cosa no es tan sencilla.
La teoría de la probabilidad actual parte de la axiomatización de Kolmogorov, auxiliada por la teoría de la medida, y es un edificio muy bien construido; eso es cierto. Sin embargo, nada dice de el origen del azar, ni de la posibilidad de que tal azar sea desconocimiento por nuestra parte, existencia de variables ocultas, o que por el contrario sea parte integrante de la estructura de las cosas.

Aunque no lo parezca, el origen de esta historia está en el “Entseidungsproblem” de Hilbert. Cuando Hilbert puso los deberes para el nuevo siglo XX, una de la cuestiones planteadas era la siguiente:

¿Todo problema matemático tiene una solución algorítmica? O en otras palabras, a todo problema especificable formalmente, ¿se le podrá dar una solución mecánica en una cantidad finita de pasos?

En 1931, el matemático austríaco-alemán Kurt Gödel dio un paso fundamental para dar una respuesta cuando demuestra el celebrado Teorema de Incompletitud , ya hemos hablado de ello en este blog. Y fue Alan Turing en 1936 quien consigue dar la respuesta definitiva a la pregunta de Hilbert: No todo problema matemático tiene solución algorítmica. Para demostrarlo inventó la noción matemática de computadora de propósito general. Básicamente, Turing define la computadora y plantea un problema sobre ella para el cual demuestra que no hay ningún algoritmo que lo resuelva. Es el problema de la detención (en Inglés se llama “Halting problem”); informalmente ya lo conocen: es el problema de saber si un programa “se cuelga” cuando corre en la computadora. El problema de la detención es indecidible, como demostró Turing.

Así pues, debemos hacer un alto para recordar una verdad que muchas veces se olvida. Haré algo de cosmética para resaltar la siguiente frase lo suficiente:

*********************************************************************
*********************************************************************


Las computadoras no se idearon para meter videojuegos, ni para chatear con los amigos: se inventaron para responder a una importante pregunta filosófica


*********************************************************************
*********************************************************************

Un matemático norteamericano de ascendencia argentina, Gregory Chaitin, pensó en este asunto en términos de azar. ¿Dónde entra el azar en todo esto? Pues muy fácil.

De la imposibilidad dada por el teorema de Turing de resolver el problema de la detención, pasamos a preguntarnos por la probabilidad de parada de un algoritmo. Cada algoritmo es en definitiva una lista finita de ceros y unos. Con unos programas (los bien constituidos), la máquina se detendrá convenientemente, y con otros se quedará colgada. Supongamos que escribimos un programa a base de n ceros y unos tirando una moneda al aire n veces, existen 2 ⁿ programas posibles. Por lo tanto la probabilidad de obtener un programa concreto de n bits es 2 ^-n. De todos estos programas, una parte muy pequeña acabarán en la instrucción “FIN DE PROGRAMA” correctamente. Sea A _n el número de programas correctos desde este punto de vista, de n bits. La probabilidad de generar aleatoriamente un programa de n bits que detenga la máquina será:

P_n= A _n· 2 ^-n.

Y si extendemos a todos los programas posibles finitos obtenemos la constante Omega de Chaitin que cabeza este artículo.

En matemáticas, a diferencia de la física, las constantes fundamentales son pocas. Tenemos el número e, tenemos pi, la constante de Euler, la de Feigenbaum y ahora tenemos la constante de Chaitin.

Existe toda una jerarquía de números en cuanto a la “maldad” que exhiben (permítanme el antropomorfismo, estamos en el post cuarentaytantos, y ya habrán aprendido a leerme entre líneas... )

Algunos números exhiben poca maldad, como los enteros. Los irracionales son bastante traviesos, y entre ellos los trascendentes son los peores. Pues bien: la omega de Chaitin es el demonio en persona.

La constante de Chaitin nos introducirá en el caos, y nos hará volver a considerar el papel del azar en el centro mismo de la matemática, terminaremos afirmando que si Dios no juega a los dados es porque está muy ocupado con la ruleta y las cartas, pero eso será en el siguiente post.

Como siempre, si ustedes quieren.

Me gustan más los anillos que los cuerpos.

Recuerdo que cuando aprendí lo que era un anillo y lo que era un cuerpo,allá por el bachiller, no supe entender la diferencia. Era evidente que había por ahí una propiedad que cumplían los cuerpos y no los anillos, pero aquello no parecía ser interesante, ni divertido. Como todo cuerpo era un anillo, parecía que los cuerpos eran más completos, y los anillos eran meros aspirantes a cuerpos.

Restringiéndonos a conjuntos de números, y simplificando un poco un cuerpo es un conjunto de números en los que podemos sumar, restar, multiplicar y dividir los elementos sin salirnos del conjunto (salvo dividir por cero, que es cosa prohibida y muy castigada). Un anillo es lo mismo, pero falla la división. Tan sólo a veces podemos dividir dos elementos del anillo sin salirnos del mismo.

Al menos debiéran haberme dicho que esa diferencia era maravillosa, y que no tenía aún capacidad de apreciarla. No me lo dijeron.
Sucede que con los anillos ocurren cosas ideales que con los cuerpos se trivializan.

En cierta ocasión, un buen amigo me regaló un libro de apariencia inocente y contenido terrible. Su título era algo intimidatorio: Algebra homológica, cohomología de grupos y K-teoría algebraica clásica

Dado que el álgebra no es mi especialidad, pude saborear aún más la diferencia entre los anillos y los cuerpos. Aprendí que un tal Alexander Grothendieck hizo cosas maravillosas antes de abandonar repentinamente y para siempre las matemáticas por asuntos políticos.

Muchas de las cosas que hizo partían de la idea de imaginar anillos donde otros habían imaginado cuerpos. Conseguía tender así puentes entre áreas dispares de la matemática: al álgebra, la geometría y especialmente la topología. Parte del secreto del asunto está en el hecho de que la estructura de anillo es la natural de los números enteros. Y todos sabemos que si dividimos dos números enteros, a veces el resultado no lo es, ¿verdad?

A pesar de todo, no tengo nada en contra de los cuerpos. Sobre todo de algunos cuerpos.

Las sucesiones de Goodstein ( y 3)

Kurt Gödel entra en escena

La demostración que hemos visto es realmente sorprendente, pero no deja (a mí al menos) una sensación de plenitud. Hemos demostrado, efectivamente que cualquier sucesión de Goodstein termina por converger a cero, pero no nos da ninguna indicación de cuándo alcanza dicho valor, ni de cómo hallarlo.

Lo primero que debemos notar es que tratándose de sucesiones de números enteros finitos todos ellos (enormes, pero finitos), hemos demostrado su convergencia a cero utilizando la noción de infinito actual (el omega w). De alguna manera; nos hemos salido del tiesto.

Esto es una constante en la matemática y no debe sorprendernos: vimos en el artículo sobre Erdös que el teorema de los números primos fue demostrado en primer lugar por De la Vallee-Poussin y Hadamard utilizando poderosas herramientas de análisis complejo que en principio nada tienen que ver con la aritmética de los enteros. Luego Erdös consiguió una demostración elemental, en el sentido de que utilizaba nada más que herramientas propias de la aritmética de los enteros, sin salirse del tiesto.

¿Ocurrirá lo mismo con las sucesiones de Goodstein? Dicho de otra forma: ¿será posible demostrar la convergencia a cero sin apelar al infinito? Al fin y al cabo, dicho infinito no se alcanza en ningún momento en el problema original...

La respuesta, rotunda como una bofetada, la dieron los matemáticos Paris y Kirby ...:NO
Estos dos matemáticos demostraron en 1.981 (Kirby, L. and Paris, J. Accessible independence results for Peano arithemtic. Bull. London. Math. Soc., 14 (1982), 285-93. ) que es imposible demostrar la convergencia a cero de nuestra sucesión sin apelar al infinito actual (la omega de los cálculos del post anterior). Ahora tenemos un teorema que demuestra la imposibilidad de demostración de otro teorema sin apelar al infinito actual.

Esto es lo mismo que afirmar que lo que afirma el teorema de Goodstein es cierto pero indemostrable dentro de la aritmética de los enteros finitos, a pesar de que no compete más que a números enteros finitos.

Es una de las poquísimas situaciones concretas en las que se ve la potencia de la maldición de Gödel.

Kurt Gödel demostró en los años 30 del siglo pasado que para todo sistema axiomático suficientemente potente como para albergar la aritmética de los enteros existen proposiciones (afirmaciones) que son ciertas pero indemostrables dentro del mismo. Esto se llama el Teorema de incompletitud de Gödel .

Dicho teorema afirma que toda teoría aritmética recursiva consistente es incompleta , y un teorema hermano dice que si una teoría aritmética es consistente, no existe en su seno demostración alguna de que efectivamente lo es . La completitud es, por tanto, la posibilidad de demostrar toda afirmación cierta. La consistencia es la ausencia de contradicción. Una teoría es contradictoria cuando se puede demostrar en su seno una afirmación y también su contraria.

Sobre el mismo se han dicho muchas cosas ciertas y muchas chorradas, y éstas últimas parece que han sido las que más éxito han tenido. El propio Roger Penrose (el gran Penrose, amigo de Stephen Hawking) hace lecturas ilícitas del mismo para arrimar el ascua a su sardina en La mente del emperador, pero este es otro tema.

Gödel demostró lo anterior de una forma demoledora: construyendo efectivamente una proposición que era a la vez verdadera e indemostrable dentro del sistema axiomático. Uno de los problemas de Hilbert quedaba zanjado de forma negativa.

Pues bien: la convergencia de nuestra serie de Goodstein es el segundo ejemplo práctico de proposiciones de Gödel en la historia de la matemática. La primera fue en 1.978, y la demostración de Kirby y Paris coloca al Teorema de Goodstein en segundo lugar.

¿Implica esto que somos impotentes para acceder a ciertas demostraciones? En principio no. De hecho, la demostración de Goodstein la tenéis en el post anterior. Sólo hacía falta añadir un axioma más a la aritmética de Peano de los enteros: el que postula la existencia de w con la aritmética ordinaria de los conocidos enteros finitos. Tenemos ahora un sistema más potente, que a su vez tendrá sus afirmaciones de Gödel ciertas e indemostrables. ¿Qué haremos entonces? Pues ampliar otra vez el sistema axiomático y vuelta a empezar. El teorema de Gödel supone una limitación a lo que podemos esperar de todo sistema axiomático, pero no impide el quehacer matemático; podemos estar tranquilos. (Bueno, supongo que muy nerviosos tampoco se habían puesto al leer esto, verdad?)
___________________________________________________________________________

Bibliografía:

Lo que he encontrado en la web sobre este tema es muy repetitivo, y creo que lo mejor está condensado aquí.

De todas formas, teneis también información en los siguientes lugares:

Algo introductorio se encuentra aquí.
Teorema de Goodstein de convergencia a cero:aquí; aquí y aquí.
En este sitio se explica que la sucesión de Goodstein de semilla 4 tiene los primeros términos 4,26,41,60,83,109,139, ...; y demuestra de forma muy sencilla que alcanza el cero en el término k = 3 x 2^402653211 -1 , aproximadamente k= 10 ^121210695 .

Las sucesiones de Goodstein (2)

¿Cómo hizo Goodstein para demostrar su teorema?

Vamos a ver el asunto, si os parece.

(Se habrá hecho algo parecido en algún blog? Miedo me da a mi aburrir al personal...) .

Para ello necesitamos un concepto adicional: las superdilataciones . Simplifiquemos la nomenclatura, y llamemos d a la dilatación u operador salto visto en el artículo anterior, reservando D para la superdilatación.

Una dilatación, como vimos ,era un cambio de p por p+1 en la expresión normal de Cantor del número, ¿verdad? Pues una superdilatación no es más que un cambio de p por w en la expresión normal de Cantor del número; donde w (omega) es el primer ordinal infinito. Nos zambullimos así en la aritmética transinfinita de Cantor. En ésta aritmética, ajena a los axiomas de Peano sobre los que se basa la aritmética de toda la vida, w simboliza el primer (menor) ordinal mayor que cualquier número natural(y por lo tanto infinito).
Lo tenemos en la imagen siguiente:



Los ordinales se ordenan de la misma manera que los enteros ordinarios, de forma que tenemos una ordenación a su vez infinita de ordinales w, w+1,...w+w=2w, 2w+1,...

Varias cosas debemos notar a estas alturas:

1.- (Esta es paradójica a tope): Si comenzamos en un ordinal infinito cualquiera, toda sucesión estrictamente decreciente llega al cero en un número finito de pasos. ¡Esto es extrañísimo! Lo que estamos afirmando es que comenzando con un ordinal infinito, llegamos al cero en un número de pasos finito necesariamente.
Esto es así por la propia definición de w. Al ser el menor ordinal mayor que cualquier número natural, cuando lleguemos a w, para seguir teniendo una sucesión decreciente, el siguiente debe ser un natural finito a la fuerza, y de éste al cero, siempre habrá un número finito de términos!!

2.- (Esta no es menos atómica). Efectuar una superdilatación, por ejemplo D₂ es lo mismo que hacer una dilatación normal d₂, seguido de una superdilatación D₃. El motivo es claro, la dilatación cambia cada p de la forma normal de un número por p+1 , y la superdilatación D₃ cambia p+1 por w . En definitiva lo único que hemos cambiado es p por w, que es precisamente el operador D₂. Dicho de otra manera: la superdilatación de un número es igual a la superdilatación de la dilatación normal de un número .Sin embargo, si en vez de dilatarlo previamente, le restamos una simpleunidad, las superdilataciones no son iguales: con una unidad menos, tenemos una superdilatación menor que antes. El motivo es claro: el 1 que restamos “pasa” al resultado, sin transformarse ni en w ni en nada!!!

Miren ahora la figura de abajo:

.

Tenemos dos sucesiones: la de Goodstein normal, y al superdilatada, cuyos miembros son los correspondientes a la anterior por el operador D. Tenemos que la segunda es estrictamente decreciente , y en virtud del punto 1, llega a cero en un número finito de pasos.

Pero resulta que el cero ¡no puede sino ser la superdilatación de otro cero!, luego acabamos de demostrar que la sucesión de Goodstein inicial converge a cero.

Basta por hoy. En el siguiente post veremos las implicaciones filosóficas de todo esto, como siempre si ustedes quieren seguirme. Son más interesantes aún que la propia demostración... y entonces será cuando el bueno de Kurt Gödel entrará en escena.

Las sucesiones de Goodstein

Este artículo intenta explicar algo muy difícil de creer. Quizás requiera un poco más de esfuerzo que el resto de los artículos hasta ahora publicados en este blog; pero intentaré hacerlo ameno. Sé (y estoy encantado por ello) que entran en este blog lectores a los que la matemática les atrae pero les asusta un poco. No quisiera que la presencia de unas cuantas ecuaciones les espante. No será esta la tónica general del blog, pero es necesario comprender que la belleza está precisamente ahí, y lo que yo hago aquí no es sino un torpe intento de expresar lo mismo en palabras.

El “aroma” de lo que ahora quiero explicar se puede percibir sin las ecuaciones, de modo que si alguien se siente cohibido, que pase de ellas y lea el resto. Antes de enfrentarnos a la maravilla, debemos repasar varios conceptos previos:

Una sucesión numérica es una secuencia infinita de números uno detrás de otro. Para tener definida la sucesión, debemos conocer la regla de generación de los sucesivos elementos de la misma. Esta definición puede darse mediante el término general , que es una fórmula en función del puesto que ocupa cada número. Sustituyendo la variable que indica el puesto por cada valor n , obtenemos el enésimo miembro de la sucesión. También puede darse recursivamente: utilizando los valores anteriores de la misma para generar los nuevos.

Ejemplo el primer caso:

A_n= 4n
Estamos ante la sucesión de los múltiplos de 4. Efectivamente, si sustituimos n por 7 obtenemos el séptimo miembro de la sucesión, que es 7 x 4 = 28.

Ejemplo del segundo caso:

A₁=1; A₂=1; A_n=A(n-2)+A(n-1)

En este caso, estamos explicando que los dos primeros miembros valen la unidad, y que cada uno de los demás es igual a la suma de los dos anteriores. Estamos ante la famosísima sucesión de Fibonacci {1,1,2,3,5,8,13,...}.

Para generar la sucesión de Goodstein necesitamos varios conceptos más:

1.- Forma normal de Cantor en base 2 de un número entero.

De la misma forma en que cualquier número lo podemos expresar como potencias de diez (Por ejemplo: 266=2x10²+6x10¹+6x10⁰), podemos hacerlo en cualquier base. Hagámoslo en base 2, obteniendo:

266=1x2⁸+1x2³+1x2¹. (Esto no es sino otra forma de decir que en base dos, 266 se escribe 100001010 .

Pues bien, la cosa es expresar como potencias de dos tanto las bases como los sucesivos exponentes, obteniendo una “torre” de exponentes. Para nuestro número 266 tendríamos:
. =
Esto es precisamente la Forma normal de Cantor en base 2 del número 266.

2.- Operador salto de base.B[b](n), u operador “dilatación”.

Dado un número expresado Forma normal de Cantor en base b , el operador salto de base sustituye cada b por (b+1). No hace falta insistir mucho para comprender que esto es una barbaridad de cambio.

Operando con el 266 obtenemos:

.

y estamos frente a un número ciertamente monstruoso. Si aplicamos a este último el operador, tendríamos un cuatro en lugar de cada tres, y la cifra obtenida simplemente escapa de nuestra comprensión de puro grande.

Con este bagaje podemos acometer las sucesiones de Goodstein.

Comienzan con una “semilla”, un número natural de cualquiera de partida que en nuestro caso podría ser 266. Este sería el primer término de la sucesión, que denotaremos G₀(266)=266.

El segundo término (G₁(266))se obtiene mediante el operador cambio de base B[2] sobre el primer término, y restando uno al resultado. Esto es: en su forma normal de Cantor, sustituimos cada dos por un tres, y al resultado le restamos una unidad. Así habríamos obtenido la sucesión de Goodstein de semilla igual a 266. Para cada entero tendríamos una sucesión de Goodstein diferente.

Veamos una recopilación de todo esto en la siguiente imagen:



Es difícil imaginar una sucesión que crezca más rápido que ésta, verdad?

Pues bien, el Teorema de Goodstein dice (y demuestra) que para cualquier valor de la semilla, toda sucesión de Goodstein alcanza... ¡¡EL CERO!!

La explicación de esta alucinante verdad es que el responsable este comportamiento es la unidad que le vamos restando a cada paso . El número de pasos necesario para que, después de un crecimiento abrumador, la sucesión vaya declinando hasta el cero es de tal magnitud que no existe forma de escribirlo, ni de calcularlo. Salvo para semillas muy pequeñas, no hay humano que lo haga, pero tampoco hay ordenador que lo pueda hacer... y sin embargo ahí está el resultado demostrado.

¿Cómo consiguió Goodstein demostrar esta cuestión?

La forma en que lo hizo hace que las sucesiones de Goodstein sean más que una simple curiosidad. De hecho, es la demostración lo importante, y lo que tiene consecuencias incluso filosóficas. Todo esto tiene relación con los infinitos de Cantor, con el teorema de Gödel y con nuestra concepción de la matemática en general. Ni más ni menos.

De todo ello hablaremos en el próximo artículo. ¿Podrán esperar?
____________________________________________________________________________________________

* La dirección de este artículo es:
http://www.infoaragon.net/servicios/blogs/tiopetrus/index.php?idarticulo=200310211

* Ver esta historia sola

Obsesión india.

Algunas civilizaciones tuvieron una verdadera fascinación por los números grandes. La civilización india fue el mejor exponente de este amor por lo desmesuradamente grande, hasta el punto de tener nombres propios para números tan inmensos que rayan en el absurdo. Estos números enormes estaban más allá de toda aplicación práctica, como Asankhyeya , que es 10 elevado a 140.

Esta cifra es inconmensurablemente mayor que el número de átomos del universo entero. El simbolismo de estos números es normalmente religioso, indicando un acercamiento a la noción de infinito; pero también estaban presentes en tratados cosmológicos. Los tratados cosmológicos de los jaina , como el Anuyogadvarasutra por ejemplo manejan potencias de diez con exponentes de 190 o incluso 250, si bien no he encontrado referencias de nombres propios para ellas.

Para los curiosos, aquí tenéis un pequeño listado de los nombres propios de algunos de estos monstruos:

Pundarika: 10 elevado a 27.
Viskhamba: 10 elevado a 47.
Sarvajña: 10 elevado a 49.
Dhavajagravati: 10 elevado a 99.
Mahakathana: 10 elevado a 126
Asankhyeya: 10 elevado a 140.

Esta obsesión por las grandes cifras contrasta con la pobreza en nomenclatura numérica de otras culturas, que no tienen nombres para designar más de unos pocos números, dejando el vago “muchos” para los más grandes.
Parece ser que los matemáticos indios estaban decididos a ganar una batalla contra sí mismos en una especie de ”a ver quién la tiene más grande” , en versión numérica. Y parece ser que lo consiguieron. Nunca es fácil asegurar una cosa de estas, pero parece ser que el Asankhyeya es el mayor número que ha recibido nombre propio en la historia de la humanidad.

__________________________________________________________________________________________

Parece ser que ha ocurrido algún problema y se han borrado las estadísticas. Afortunadamente se han podido recuperar todos los artículos y vuestros comentarios. Lo cual es una suerte, porque los comentarios son parte importante de este vuestro blog.