Conceptos

¿0+0+...=0?

¿Se puede obtener algo a base de sumar cantidades nulas?

La pregunta parece ridícula...

Vayamos aproximándonos a la respuesta. Para empezar, si sumamos un número muy grande de cantidades muy pequeñas, podemos obtener cualquier cosa. Si el número de cantidades que sumamos tiende a infinito y el valor de cada cosa tiende a cero, estamos en la misma situación. Es lo que en el cole repetíamos; aquellos de cero por infinito es indeterminación .

Lo que queríamos decir con aquella frase no es sino algo obvio: cantidades muy pequeñas pueden dar como resultado cualquier cosa a condición de sumar las suficientes de ellas.Nada que viole la intuición ni las buenas costumbres.
Ya saben ustedes: tacita a tacita...

No es eso de lo que quiero hablar ahora. Quiero que las cantidades no sean despreciablemente pequeñas; quiero que sean estrictamente nulas. Cero patatero.

Ahora la cosa cambia, verdad?

En una primera aproximacion admitiremos que por mucho que añadamos nada a la nada que tenemos, seguiremos teniendo nada; y sin embargo, esto no es así. Todo depende de cuántas cantidades nulas estamos sumando.

Si la cantidad es finita; no hay nada que hablar: el resultado es cero. Si la cantidad es infinita, pues también. Puedo estar eternamente añadiendo ceros, que el resultado será siempre nulo. ¿O no?

Pues siento si rompo algún esquema, pero depende.

Recordarán si leyeron el artículo anterior, que había infinitos e infinitos. Si añadimos una cantidad infinita pero numerable (aleph-cero) de ceros, nuestra intuición sigue siendo correcta: resultado nulo. Pero si la suma se extiende a una cantidad no numerable de elementos (aleph-uno), la verdad es que podemos obtener un número tan grande como queramos, aunque cada uno de ellos sea estrictamente cero.

Tal es la potencia del primer infinito no numerable. ¿Les parece mentira? Fíjense en la figura. Tenemos un segmento de recta comprendido entre los puntos 0 y 1. Existe una noción muy concreta de medida para los conjuntos de elementos, que se llama medida de Lebesgue . Para nuestros propósitos actuales esta medida es idéntica a la longitud del segmento. Estaremos todos de acuerdo en que el segmento mide 1, y en que está formado por puntos. También estaremos de acuerdo en que la longitud de cada punto es EXACTAMENTE CERO. Pues eso, que la suma de todos esos ceros da uno.

Como vimos en el artículo anterior, el número de puntos de un segmento no sólo es infinito, sino que es un infinito no numerable, y ese es el quid de la cuestión.

______________________________________________________________________________________

PD. En una ocasión intenté convencer a un contertulio de esto que acabo de comentar, y no sólo no se lo creyó, sino que encima se enfadó conmigo. Espero que eso no me pase con ustedes...

Aleph

Miren un momento el símbolo que encabeza este artículo. Se trata de la primera letra del alfabeto hebreo; aleph . Detrás de este símbolo está el concepto más abismal de toda la matemática: el infinito, y un hombre: Georg Cantor.

Los números grandes nos abruman: el número de estrellas en el universo, la cantidad de granos de arena de todas las playas, el número de mentiras que nos cuentan los políticos, el número de partículas elementales del universo... sin embargo todos estos números son finitos.

Alexander Grothendieck decía que muchas de sus grandes ideas eran en realidad cosas muy sencillas; ramplonas incluso. Esas, cuando funcionan, son las grandes ideas que abren nuevos caminos. Georg Cantor tuvo una idea de este estilo, idea que he visto con mis propios ojos emplear a un niño de menos de un año.

Si un niño que no sabe contar tiene que elegir entre dos conjuntos de caramelos o de pequeños juguetes, es muy probable que comience a emparejarlos hasta que sobren los de una clase cuando están ocupados todos los de la otra. De esta forma, sabe qué conjunto es el mayor, y se lo queda. Cantor tuvo la idea de hacer lo mismo para comparar el tamaño (la potencia) de conjuntos infinitos. Si se podían poner relación uno-uno, es que eran del mismo tamaño. La cosa no parece muy revolucionaria, pero debéis pensar que a priori, parecería que dos conjuntos, por el hecho de ser infinitos, van a ser igual de grandes . Plantear siquiera el método de Cantor supone no aceptar esta intuición.

Uno de los primeros resultados de este método de conteo es que un conjunto infinito puede ponerse en relación uno-uno (biunívoca) con una parte de sí mismo. En efecto, tomemos el conjunto N de los naturales, y el conjunto M de los múltiplos de un millón. Es del todo evidente que a cada natural le corresponde un número de millones igual al valor de dicho natural, luego ambos son de mismo tamaño. De hecho, esta será a partir de ahora la caracterización de un conjunto infinito: un conjunto es infinito si y solo si puede establecerse una aplicación biunívoca entre él y un subconjunto de sí mismo.

Si esto les parece extraño, agárrense, porque lo peor está por llegar.

El resultado anterior en el fondo nos tranquiliza. Si N es del mismo tamaño que M, parece apoyar la idea de que dos conjuntos, siendo infinitos ambos, son del mismo tamaño, aunque M tenga un elemento por cada millón de elementos de N. Pero Cantor demostró que hay infinitos más insondables que el conjunto de todos los infinitos números enteros. Demostró que el conjunto de los números reales R es tan grande que su potencia es incomparable con la de N. No se puede numerar el conjunto R. De hecho, un minúsculo intervalo de R [0,e], donde e es positivo tan pequeño como queramos tiene un número insondablemente mayor de elementos que el infinito, inacabable, abrumador, inmenso conjunto N.

La demostración por el método diagonal original de Cantor la podeis encontrar sin dificultad en la red; por ejemplo aquí. pero una bonita demostración alternativa la teneis aquí.

La intuición se nos rompe cuando nos enteramos con Cantor de que el conjunto de los racionales, a pesar de ser tan denso, es de igual tamaño que N , y por lo tanto numerable; al igual que el conjunto de los números algebraicos de los que hemos hablado en otro post. El monstruoso tamaño de R se debe pues a los irracionales trascendentes ( no algebraicos). El infinito de toda la vida es una mierdecilla al lado de este nuevo infinito, como podéis ver.
Cantor había demostrado que hay infinitos e infinitos. Puesto que unos eran mayores que otros, se podían ordenar. Llamó Aleph-cero a la potencia de N y Aleph-uno a la potencia de R . Conjeturó además que entre ambos no había ningún numero transinfinito.(Hipótesis del continuo).

Si no han notado aún un escalofrío en la espalda al enfrentarse con Aleph-uno lean lo que sigue.

Cantor demostró que podía ponerse en relación biunívoca el conjunto de los puntos de una recta y el conjunto de los punto de todo el plano. “Lo veo y no lo creo” exclamó. Había demostrado que la potencia de R era idéntica a la de RxR , lo cual nos indicaba ciertamente que el espacio tridimensional euclídeo tenía la misma potencia. Esto es alucinante, y si no se sorprenden, es porque ya lo sabían, o porque no lo han entendido.
Dado que es muy fácil comprobar que un insignificante segmento tiene tantos puntos como la recta entera, resulta que el número de puntos de un segmentillo es igual al número de puntos del universo entero, considerado este como un espacio infinito tridimensional (o tetradimensional, no importa!!!).

¿Comprenden ahora la inmensidad de Aleph-uno ?

Parece ahora que nada pueda ser estrictamente mayor... pues bien: existe Aleph-dos; y hace que Aleph-uno palidezca como una damisela avergonzada. La jerarquía de monstruos transinfinitos es a su vez infinita.

Cantor intentó concebir el infinito de todos los infinitos, pero su mente se quebró. Yo no creo que fuera por esto, sino que el pobre andaba con muchos problemas mentales, pero la leyenda alimenta la idea de que se acercó demasiado a la verdad, como una polilla a la luz, y se quemó. Una bonita leyenda, sin más.

Cantor murió loco, escribiendo tratados religiosos y sin ser reconocido por la comunidad matemática. Hoy es uno de los pilares de la matemática moderna, hasta el punto que Hilbert exclamó en una ocasión:

“Nadie nos expulsará del paraíso que Cantor ha creado para nosotros”

pero esa es otra historia que me da para otro post. Si ustedes quieren, claro está.

Intuiciones y mentiras.

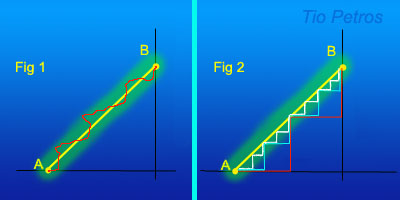Una constante en este blog será la insistencia en que la intuición por sí sola no es una buena guía en matemáticas. Afortunadamente, tenemos una herramienta que nos sirve de brújula: el razonamiento riguroso. Lo que sigue es una muestra de los errores de la intuición, que son siempre debidos a dar por sentado cosas que no son ciertas; quizás porque tenemos una tendencia mental a extrapolar nuestras vivencias diarias a lugares en los que las cosas son ligeramente más complicadas.

Miren ustedes la figura 1. Tenemos una recta que une los puntos A y B, cuya longitud es raíz de 2, en virtud del teorema de Pitágoras. Imaginen una banda de espesor e centrada en la recta AB. Consideremos todos los posibles caminos de A a B, completamente en el interior de la banda, que no tengan retrocesos. Unos serán más largos que otros, y el camino recto será, lógicamente el más corto. El que aparece en rojo en la figura es uno de los posibles.

Razonemos con “sentido común”:

Si vamos disminuyendo el espesor e de la banda, vamos obteniendo caminos cada vez más cercanos a la recta. Si el espesor de la banda tiende a cero, los caminos tenderán a la recta, y la longitud de los mismos tenderá a raíz de 2.

Podemos entonces enunciar la siguiente conjetura:

La longitud del camino más largo de A a B en el interior de una banda de espesor e centrada en la recta AB tiende a la longitud AB cuando el espesor de la banda tiende a cero.

¿Existe algo más lógico, coherente con nuestra experiencia cotidiana y racionalmente satisfactorio?

Pues bien, todo es mentira. Lo anterior es una llamada a la buena voluntad y al sentido común del futuro creyente en la conjetura, no una demostración. Y en matemáticas esto no sirve.

De hecho, existen caminos de longitud exactamente 2, mucho mayor que la distancia AB para cualquier espesor de la banda. Esto parece una afirmación extraordinaria, y en parte lo es pues parece contradecir el sentido común.

Afirmaciones extraordinarias requieren pruebas extraordinarias .

¿Con qué tipo de prueba podría un matemático avalar esta afirmación? Demostrar la falsedad de una conjetura admite dos estrategias: demostrar desde la generalidad que si fuera cierta, se caería en una contradicción (reducción al absurdo) o poner un contraejemplo.

Haremos lo segundo. Fíjense en la figura 2.

Tenemos una camino de A a B que va en horizontal hasta el origen y sube verticalmente hasta B, de longitud 2. Podemos complicar este camino añadiendo escalones intermedios, como se ve en color rojo , verde y blanco. Si repetimos este proceso, obtenemos caminos de A a B, todos ellos de la misma longitud 2. Por pequeño que sea el espesor de la banda, siempre podremos hacer que todo el camino esté dentro de ella. En el límite, a pesar de tener un camino infinitamente próximo a la recta AB, no es cierto que este camino comparta las propiedades de la recta: sigue siendo de longitud 2. Es una “curva” con infinitos puntos de no derivabilidad que nada tiene que ver con una recta, a pesar de su infinita proximidad.

La existencia de estas funciones "patológicas" tiene un puesto de honor en la historia de la matemática, y da paso al tópico por excelencia de la última década en matemáticas: los fractales.
_________________________________________________________________________________________________

El estudio de las funciones entre dos puntos dados que cumplen determinadas propiedades dio paso a la revolucionaria idea de espacios matemáticos en los que sus “puntos” no son los puntos del espacio, sino las propias funciones. Así nació el cálculo funcional, en el que se manejan espacios de infinitas dimensiones, fecundo campo de investigación matemático a lo largo de todo el siglo XX, cuyo origen podemos datar en los mismos nacimientos del análisis. Banach y Hilbert sentaron las bases modernas de los espacios normados y métricos generales, y hoy en día plantean multitud de problemas analíticos y sobre todo topológicos pendientes de resolver.

Confundir media y mediana, ¿es una moda?

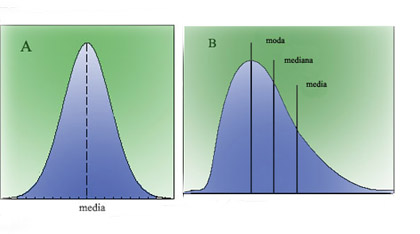Una de las formas más inconvenientes de buscar información fidedigna es buscarlo en internet. En otra historia comentábamos que dado que en el desarrollo decimal de pi está TODO, es lo mismo que decir que no hay nada. Nuestra querida web, en la que tantas horas metemos pone a nuestra disposición una parte importante de totalidad del saber humano, así como una gran parte de la imbecilidad humana. Al faltar un criterio de decisión fidedigno, estamos perdidos. Me gustaría poder decir que lo que ustedes lean aquí es básicamente correcto y honradamente escrito, pero al fin y al cabo, ustedes me encontraron en la calle. No se crean nada de lo que pone aquí, ni en ningún otro ciberlugar. Al menos, mantengan activa la hipótesis nula de que la web no es un buen lugar para buscar la verdad, sobre todo si no saben quién la ha escrito. Estaría bien recordar que hace muy pocos años; allá por la prehistoria, los escritos no firmados eran simplemente ignorados...

Todo esto viene a cuento de una frase que leí una vez en mi impulsivo navegar, y no he sido capaz de contrastar, ni de volver a encontrar. Esta frase me da pie a un artículo para el blog, así que lo contaré igual. No importa que sea cierta o no porque mil veces ocurren anumerismos similares, y lo importante es la reflexión subsiguiente, no la veracidad de la anécdota. Por lo tanto no mencionaré el país, ni el presidente concreto al que se atribuía la frase, que era más o menos esta:

El presidente se ha mostrado muy consternado al comprobar el resultado de una estadística fiable, según la cual la mitad de los ciudadanos tiene una inteligencia por debajo de la media.

No soy capaz de recordar si era inteligencia, nivel cultural u otra cosa similar, en todo caso era una cualidad positiva la que se estaba midiendo.

El resto de la noticia era una mofa hacia el compungido presidente, que se podía resumir así: ¡Qué burro el presidente, no sabe que por definición de la media, eso debe ocurrir necesariamente!

Es una confusión muy común. Además socialmente es muy excusable. Hoy en día es incluso de buen tono exhibir ignorancia en cuestión de números, y no digamos de estadísticas. En sin embargo ahí donde nos engañan todos los días. El anumerismo (de los demás, claro está) es una de las mejores herramientas de manipulación.

En el caso que nos ocupa, a mi no me queda claro que la estulticia presidencial estuviera por encima de la media, ni que la del comentarista estuviera por debajo.

Para empezar, debiera comentar que la intuición no es una herramienta de fiar en matemáticas. Es tan importante como la inspiración en los poetas, pero no más. No creo que con inspiración se pueda componer una gran obra, sino con mucho trabajo y sudor. Posiblemente el presidente caía en un error, pero el comentarista caía en otro con total certeza. Vamos a explicarlo.

Debido a una cosa muy interesante y muy profunda de la que me gustaría hablar otro día y que se llama el Teorema central del límite , estamos acostumbrados a las distribuciones simétricas, como la de la figura A. En ellas coincide la media ( que todo el mundo sabe lo que es), la moda (que es el valor con mayor frecuencia observado) y la mediana, que es el valor que deja tantas observaciones por arriba como por debajo. Si la distribución no es simétrica, tenemos situaciones como la de la figura B. La media está desplazada respecto a las demás medidas centrales, y es claro que en este segundo caso más de la mitad de la población está por debajo de la media. Siempre será la mediana, por su propia definición la que estará centrada respecto al número de observaciones a ambos lados, no la media.

¿Tenía nuestro hipotético presidente motivos de pesar?

Pues según se mire, sí. Si la distribución hubiera sido asimétrica en sentido contrario a la de la figura B, más de la mitad de la población hubiera tenido una inteligencia, cultura o educación superior a la media, puesto que la mediana sería de valor superior a la media. Esto supone un desplazamiento de la masa total hacia valores más altos, y es claramente positivo para la población, si el parámetro que se mide es una cualidad positiva para la misma. Eso no se producía, pues la noticia implicaba una distribución simétrica.

¿Se refería a eso el presidente? Lo dudo.
¿Tenía motivos de mofa el comentarista? Pues realmente, si los tenía no era por lo que él creía...

Probabilidades extrañas

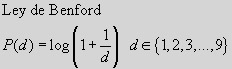Los matemáticos se parecen a los niños en muchos aspectos. No hay nada que impulse tanto al trabajo como una pregunta sin responder. ¿Y eso porqué? parece ser la pregunta preferida. Algo así es lo que debió sentir el bueno de Simon Newcomb allá por 1.881 cuando observando distraídamente su libro de tablas de logaritmos, se dio cuenta de que estaba mucho más desgastada por las primeras páginas que por las últimas.

Newcomb era astrónomo y matemático, y por aquella época, las tablas de logaritmos eran el libro de cabecera de cualquier manipulador de cifras que se preciara. El desgaste diferencial del libro sólo podía tener una explicación: a lo largo de los años había consultado mucho más el logaritmo de los números que comenzaban por 1 que de los que comenzaban por números más altos.

Aquello parecía una hipótesis extraña: ¿porqué iban a ser más abundantes los números cuya primera cifra es 1, ó 2 que aquellos que empezaban por 8 ´0 9?

Nuestro astrónomo no pudo dar con razón alguna: sus números provenían de la observación de los astros principalmente: eran números sacados del espacio físico, y no debían tener ningún sesgo en su primera cifra. Se limitó a constatar que “la ley de probabilidad de ocurrencia de números es tal que las mantisas de sus logaritmos son equiprobables”.

El asunto no avanzó mucho hasta 1.938; año en el que el físico Frank Benford estudió 20.229 números provenientes de 20 muestras variopintas: constantes y magnitudes físicas, longitudes de ríos, direcciones de personas... incluso cifras sacadas de portadas de revistas. A partir de los datos extraídos del mundo real, postuló la llamada “ley de los números anómalos de Benford”expresable por la fórmula que abre este artículo.

Podemos ver en una gráfica las probabilidades de ocurrencia de cada dígito en primera posición, y veremos que la unidad ocurre casi un tercio de las ocasiones, y el 9 no llega al 5%.



Los números obtenidos del mundo real suelen ser dimensionales: podemos estar hablando de la renta per cápita de los nepalíes medida en rublos, de la superficie de los cráteres lunares en pies cuadrados o de la edad de los árboles de un bosque en quincenas. Si la distribución de Beford aparece en todas ellas, es evidente que debe ser invariante por cambio de escala. Si multiplicamos todos los datos por una constante, no se modifica la ley de aparición de la primera cifra. Por eso, son indiferentes las unidades de medida utilizadas. Esto es menos trivial de lo que parece: si multiplicamos por dos, todos los unos de primera cifra, que serán el 30% se nos van al garete; pero la cosa se compensa pues los cincos, seises, sietes, ochos y nueves...¡se convierten en unos!

Está claro que no siempre aparece esta ley: si tomamos los teléfonos de una provincia, no la encontraremos; y si medimos la longitud de las calles de una ciudad racionalmente urbanizada de cabo a rabo, tampoco: es donde más azar existe donde más fácil la encontramos.

¿Porqué funciona la ley de Benford en el mundo real¿

Se me ocurre un ejemplo para ver una explicación, sacado de la vida real:

Supongamos que en correos hacen una estadística sobre los números de portal de los destinatarios de las cartas a nivel nacional. Si todas las calles tuvieran 99 portales, 11 de ellos empiezan por 1 ( el portal 1 y los portales del 11 al 19) lo mismo podríamos decir de todos los demás números. Pero es que las calles tienen cada una un número de portales distinto; si la calle tuviera 19 portales, de ellos 11 empiezan por 1!!!

Vemos pues que salvo calles excepcionales de 9, 99, 999 portales, todas las demás favorecen los primeros dígitos pequeños, algunas extraordinariamente. Por ello, el fenómeno observado tiene su origen en la contribución de todos los casos posibles... y es la ley logarítmica de Benford.

En una ciudad artificial, que se hubiera construído racionalmente, con calles idénticas de 99 portales esto no ocurriría, pero la realidad es más compleja, y esta complejidad favorece a la ley de Benford.

Hay otro motivo matemático, pero es de bastante alto nivel. Sucede que la distribución de tiene una propiedad curiosísima: si un determinado fenómeno tiene n causas aleatorias y una de ellas sigue la distribución de Benford, la general también. La distribución de Benford es una especie de distribución que contamina a las demás. Así pues, cuanto más batiburrillo haya en la generación del fenómeno y más complejo e intratable sea, más fácil es que aparezca el 1 en primer lugar de los resultados obtenidos.

De hecho, existe una técnica de detección de fraude en declaraciones de renta basada en esto: si donde debiera aparecer Benford no aparece es un síntoma (que no una demostración categórica) de que los datos han sido amañados.

Para saber más podeis consultar aquíen castellano y
aquí en inglés.

Mensajes ocultos en pi

Un número trascendente es un número real que no es raíz de ningún polinomio. Los que sí lo son se denominan algebraicos, y pueden ser tanto racionales como irracionales. Es curioso que siendo tan grande el número de polinomios posibles (de cualquier grado), casi todos los reales son trascendentes.

Esta último frase parece vaga y fuera del rigor matemático (“casi todos”), pero no lo es en absoluto. Cuando decimos que “casi todos” los reales cumplen una propiedad, cuando decimos que una propiedad se cumple casi por doquier, o cuando decimos que un suceso se producirá casi seguro estamos afirmando que tal cosa se cumple, o se produce para todo número, en todo punto o en todo caso excepto en un conjunto de medida cero. Y es que una vez más, la teoría de la medida está detrás de este asunto.

El motivo por el que casi todo número real es trascendente es que el conjunto de todos los polinomios es numerable, y como cada polinomio tiene una cantidad numerable de raíces, el conjunto de éstas también lo es. Dado que el conjunto de los reales NO es numerable, la potencia de los trascendentes es mayor, y de hecho, copa toda la medida de R. Los algebraicos son humo fractal dentro de los reales.

Nuestro protagonista, pi; además de trascendente parece ser que es normal, lo que quiere decir que en su expansión decimal, los diez dígitos aparecen con igual frecuencia. Esto es una conjetura pendiente de demostrar. Demostrar la normalidad de un número no es cuestión sencilla. No obstante, el número de decimales conocido demuestra que la truncación de pi a esos decimales es normal. La verdadera sorpresa sería la demostración futura de la no normalidad de pi.

Pues bien; toda esta introducción viene a propósito de la existencia de mensajes en el interior de pi. Que yo sepa, la popularización de esta idea viene de la novela CONTACT, de Carl Sagan, pasada al cine con relativo éxito con la cara amable de Jodie Foster. Actualmente existe gente buscando mensajes extraterrestres en el interior de pi, o incluso mensajes de Dios.Lo curioso es que estos mensajes realmente existen dentro de pi. Vamos a explicar porqué.

Admitamos la conjetura de normalidad en pi. La infinita ristra de dígitos de la expansión decimal es aleatoria, en el sentido de que tiene las mismas propiedades que una ristra conseguida al azar. Imaginemos que estamos buscando una secuencia concreta de n dígitos en pi. Tomada una secuencia cualquiera de n dígitos, la probabilidad de que coincida con la que buscamos es de una entre 10 elevado a n. Probabilidad pequeña para n grande, pero mayor que cero. Es muy fácil demostrar que un suceso de probabilidad mayor que cero llega a producirse si se efectúan suficientes pruebas, de hecho, se produce infinitas veces si las pruebas son infinitas . Así pues, podemos asegurar que tal secuencia existe realmente en algún sitio dentro de pi. Lo extraordinario sería que no existiera, suponiendo la normalidad de pi.

Así pues, la codificación completa de “Lo que el viento se llevó” en estéreo y en idioma bantú está dentro de pi, además está infinitas veces, incluso con finales espurios en los que los protagonistas se quedan juntos. También está el número de la lotería de la semana que viene, la historia universal del siglo XXII, y este mismo artículo que estoy escribiendo ahora. Así como todas las historias, novelas y poemas producidos por la humanidad, que no son sino ristras de n dígitos en algún código.

El gran Kolmogorov postuló como definición de complejidad de un objeto matemático la longitud de mínimo algoritmo necesario para producirlo. Pi puede generarse con programas muy cortitos, luego encierra muy poca complejidad, y por tanto poca información. ¿Cómo podemos conjugar ambas visiones tan contrapuestas en apariencia.?

Se me ocurre una forma muy sencilla de verlo. Hace poco ví en la red un archivo con el primer millón de cifras de pi. Busqué en su interior mi número de teléfono(sin prefijo) usando Edición/buscar con el word de Microsoft, y ¡allí estaba!

Puedo dar mi teléfono de dos formas: comunicando las seis cifras del mismo, o diciendo el puesto del primer dígito del mismo en el desarrollo de pi. Pero para ambas cosas necesito el mismo número de cifras, puesto que mi teléfono se encontraba hacia la mitad del primer millón de dígitos, luego no ahorro información. La codificación de la película mencionada más arriba comenzará en un puesto tal que necesitaré aproximadamente la misma cantidad de dígitos para decirlo que para tener la película codificada por otro medio. Ahora es más fácil comprender que pi no encierra mucha información. Al estar TODO en pi, no hay nada en pi.

Decididamente, pi es fascinante, pero no es en la posible existencia de mensajes ocultos donde reside la fascinación.

Lo preocupante es que algún día alguien encontrará el puesto en el que comienza alguna codificación de la frase “Yo soy el camino, la verdad y la vida” en hebreo, y entonces, a ver quien es el guapo que consigue convencer a la gente que nosotros ya sabíamos que esa frase estaba dentro de pi, pero que no significa nada.

La entropía de Kolmogorov

Para un servidor una de las mayores incógnitas del concepto de entropía es el motivo por el que tantas veces se emplea como comodín para las más peregrinas explicaciones. El concepto tiene un feeling indiscutible, pero lo malo es que transciende al mundo coloquial sin rigor alguno. Es de “buen tono” introducir la palabra entropía, aunque no se sepa muy bien a qué nos estamos refiriendo. Así, pude oír hace algunos años al escritor Fernando Sánchez Dragó manifestarse contra las corridas de toros porque añadían sufrimiento a la entropía del universo. El concepto al que hacía referencia de forma inadecuada, pueril y sin rubor alguno era evidentemente el concepto físico. En este ámbito, si un tertuliano quiere destacar no tiene más que unir el vocablo ciertamente eufónico de entropía al vocablo universo para obtener ...una frase redonda sin sentido alguno. (Me temo que este comentario es un poco off topic en Tio Petros).

Tenemos también el concepto de entropía en laTeoría de la información de Claude E. Shannon. Es una extrapolación del concepto a otro ámbito, y tampoco de esta entropía queremos hablar ahora.

Cuando Shannon publicó sus trabajos hacia 1.948, a los matemáticos en general les pareció algo excesivamente orientado a la tecnología como para tener interés en matemática pura. El gran Andrei Nikolaievich Kolmogorov fué la excepción, escribiendo en una ocasión:

“La importancia del trabajo de Shannon para los matemáticos puros no fue totalmente apreciada desde el comienzo. Recuerdo cuando, en el Congreso Internacional de Matemáticos celebrado en Ámsterdam en 1.954, mis colegas norteamericanos, especialistas en probabilidades, creían que mi interés por los trabajos de Shannon eran algo exagerado ya que esto era más tecnología que matemática. Ahora, tales opiniones ni siquiera necesitan ser refutadas”

De esta forma, y dada la inmensa y merecida reputación de Kolmogorov, le fue posible extender las nociones de Shannon a la matemática más abstracta. Concretamente estableció la definición de entropía en el interior de un conjunto.

Dado un conjunto, es necesario utilizar cierta cantidad de información para delimitar sin ambigüedad cualquiera de sus subconjuntos propios. Kolmogorov entendió que aquí era donde podía entrar el concepto de entropía. Definió la entropía de un subconjunto en función del hecho anterior, y la llamó e-entropía. (Léase épsilon-entropía).

Si C es un conjunto finito, podemos expresar por enumeración la lista de sus subconjuntos. A cada subconjunto le corresponderá simplemente su número de orden en la lista. El tamaño de la lista es de 2 elevado a N subconjuntos. Lo que expresado en sistema binario nos ocupa precisamente N bits. (Otra forma de verlo es teniendo en cuenta que podemos hacer corresponder un bit a cada posible elemento de los N en C , y para un subconjunto concreto, el j-ésimo bit vale 1 si está presente en el subconjunto, y 0 en caso contrario).

Kolmorogov definió la entropía de un subconjunto como

H(C)= log (N)

donde el logaritmo está en base 2.

Para conjuntos no numerables su táctica fue el uso de e-recubrimientos de radio e (épsilon) arbitrario. La epsilon-entropía del subconjunto era al igual que en el caso numerable, el logaritmo en base 2 del número de elementos del e-recubrimiento mínimo para cubrir totalmente al conjunto. Un e-recubrimiento del conjunto C es un recubrimiento por conjuntos de diámetro menor o igual a 2e. En el caso se un segmento de recta, el número de elementos de un e-recubrimiento es precisamente (L/2e), de donde su e-entropía será:

H(C)=log (L/2e) , fórmula que adorna la foto que encabeza este artículo, en la que aparece el gran Kolmogorov, de quien nos ocuparemos en un artículo futuro.

De esta manera, Kolmogorov hecha un puente entre la teoría de la información y la abstracta teoría de conjuntos.

La paradoja de Tarski - Banach

Las paradojas no existen. Existen resultados que nos parecen paradójicos por que habíamos supuesto erróneamente que el resultado iba a ser otro. Y es que a partir de cierta hondura matemática, la intuición suele ser mala consejera.

La llamada paradoja de Tarski-Banach dice la siguiente barbaridad:

“Es posible partir una esfera maciza en seis trozos disjuntos de forma que recomponiéndolos mediante movimientos rígidos obtengamos dos esferas macizas de las mismas dimensiones que la original”.

Este enunciado y su demostración fue presentado en 1.924 por los matemáticos Alfred Tarski y Stephan Banach. En 1.944 el número de piezas fue reducido a cinco por R.M.Robinson, y en la actualidad bastan cuatro a condición de olvidarse tan sólo del punto central de las esferas.

¿Dónde está el truco? Bueno, en realidad las demostraciones son rigurosas y habría que decir que no hay truco; sin embargo el asunto va contra todas las intuiciones que uno pueda tener. Para empezar, si las esferas son materiales, y no ideales, estamos ante una violación del principio de conservación de la materia. Dado que no es probable que el proceso de partición implique reacciones nucleares, la materia debería conservarse...

Olvidémonos por un momento de esferas materiales y pensemos tan solo en subconjuntos del espacio ordinario tridimensional en forma de esfera. Aunque no lo mencionemos, estamos en terrenos de la Teoría de la medida. Todo el mundo tiene nociones intuitivas de lo que es una medida: es un número asociado a un objeto que indica la cuantización de alguna de sus propiedades; el volumen en este caso. Toda medida que se precie debe tener tres propiedades de “sentido común”, sin entrar en los formalismos de la Teoría de la medida:

1.- No puede ser negativa.
3.- Debe ser invariante por movimientos rígidos.
2.- Debe ser aditiva. (Esto quiere decir que la medida de la unión de varios objetos sin partes comunes debe ser igual a la suma de las medidas de los objetos por searado).

Siendo así, parece una aberración la afirmación de Tarski y Banach. ¿Hay una explicación satisfactoria de este resultado?

Bueno, la buena noticia es que hay explicación, y la mala es que no es satisfactoria (al menos para un humilde servidor).

La culpa la tiene el axioma de elección, que dice la "obviedad" siguiente:

Si tenemos una colección A de conjuntos no vacíos, es posible formar un conjunto tomando exactamente un elemento de cada uno de los conjuntos que forman la colección A.

Pues bien, utilizando dicho axioma, cuya consistencia con la Teoría de Conjuntos ha sido probada, es posible demostrar que existen subconjuntos no medibles en la recta R, en el plano y por extensión en el espacio tridimensional. Pero entiendanme bien, por favor: “no medible no quiere decir de medida cero, como un punto: no medible quiere decir que no se le puede asociar ningún valor a la medida.

Además, la demostración de esto último es constructiva: se construye un subconjunto que no puede tener por su propia construcción ninguna medida asociada. Esto se hace utilizando el axioma de elección.

Ahora podemos comprender que si podemos partir una esfera en trozos no medibles, la aditividad de la medida de volumen se nos va al traste. ¿Porqué tendrían que cumplirla unos trozos que nada saben de medidas? Lo que consiguen Tarski y Banach sobre el papel y en teoría es trocear una esfera de forma que los trozos no son medibles. Esto no deja de ser un experimento mental, desgraciadamente: las formas deben ser irrealizablemente complejas para ser no medibles; algo tan imposible de realizar en la práctica como esculpir un conjunto realmente fractal...

En este direcciónteneis un maravilloso libro de texto sobre Teoría de Conjuntos y lógica matemática. Allá se habla con extensión y enorme rigor de los axiomas de la teoría de conjuntos y sus aplicaciones. Es gratis bajarlo, pero no sale gratis comprenderlo. Si bien no es necesario ningún conocimiento previo, requiere un gran esfuerzo... pero algunos pensamos que merece la pena.
Sobre la paradoja de Tarski-Banach no he encontrado en la red nada interesante, más allá de cuatro tópicos. Si algún lector sabe alguna dirección complementaria a lo que aquí se ha dicho, sería de agradecer que la expusiera en los comentarios.

Hormigas computacionales.

Uno de los problemas básicos en matemática es el de optimización. Encontrar el punto en el que una determinada función alcanza el máximo (maximización) o el mínimo (minimización). Es tan obvio el interés de las técnicas de optimización que no vale la pena insistir en ello. Sin embargo, el problema es muy general, y no admite un tratamiento global. Para empezar, “el punto” que se quiere encontrar puede ser cualquier cosa, dependiendo del problema. Los alumnos de bachiller hallan puntos en los que una función real de variable real tiene un extremo, pero la vida real es mucho más diversa. Vamos a hablar de un problema concreto que es un paradigma de complejidad computacional: el Problema del Agente Viajero, conocido en computación como el problema STP, por sus siglas en inglés.

Un agente debe recorren n ciudades, y entre los posibles recorridos, debe elegir el más corto que pase por todas ellas para volver a la primera. Se conoce la matriz de distancias cruzadas entre las n ciudades, obviamente. Es muy fácil hacer un programa que de con la solución óptima: existen n! recorridos, y si no es importante la ciudad de comienzo (n-1)! recorridos diferentes. Basta hallar la distancia de todos los caminos posibles y tomar el mínimo. El problema es que la función factorial crece endiabladamente, y con un puñado de ciudades necesitaríamos años de computación para encontrar el camino más corto. Con sesenta ciudades, el número de caminos es comparable al de partículas atómicas del universo, y procesando un billón de ellas al segundo necesitaríamos más tiempo que la edad del cosmos para computarlas todas. No se conocen algoritmos que den la solución en tiempo polinómico (pero esa es otra historia que contaremos más adelante). Es evidente que necesitamos atajos.

Afortunadamente, estos existen, y sin bien no necesariamente nos proporcionan el óptimo, nos devuelven soluciones cercanas en tiempos aceptables. Vamos a hablar de uno de ellos, vistoso a más no poder, y de buenos resultados. Está inspirado en la naturaleza debido a la obviedad de que la evolución biológica lleva miles de millones de años ensayando estrategias para solucionar problemas (perdónenme los lectores la personalización de la evolución como algo capaz de tener intenciones y deseos de solucionar cosas, nada más lejos de mi intención; es sólo una metáfora).

Aquí es donde entran las hormigas. Cuando estos himenópteros van de un lugar a otro, podemos comprobar que siguen caminos muy cercanos al óptimo. Si un obstáculo impide el paso normal, tras ciertos titubeos iniciales se termina por rodear el obstáculo por el camino más corto. ¿Cómo lo consiguen?

La respuesta es decepcionante de puro simple. No hay inteligencia alguna tras esto: las hormigas siguen el camino de sus predecesoras porque huelen las feromonas que éstas van depositando a su paso. Ante una bifurcación, tienden a elegir el camino de más olor a hormiga. Entre varios caminos alternativos el más corto o más fácil estará más transitado por ser necesario menos tiempo en recorrerlo, y por ello, la exploración de los otros más penosos es un fenómeno transitorio: cada vez más hormigas tenderán a recorrer el más transitado, creando una realimentación positiva que solo cesará cuando los demás caminos sean olvidados. Además, las feromonas son volátiles: en cierto tiempo no quedará rastro de otro camino que el óptimo.

¿Cómo funciona un algoritmo de búsqueda basado en hormigas? Pues se ponen cierto número de “hormigas” a recorrer caminos entre las ciudades. Cada hormiga desde una ciudad elige la próxima de forma probabilística (las ya visitadas están excluidas de la búsqueda en cada ciclo) en función de la distancia entre sus vecinas, premiando las más cercanas ( es evidente que el recorrido óptimo no irá saltando entre ciudades lejanas unas de otras, pero no es claro que debo elegir siempre la más cercana, no mucho menos) y en función de la cantidad de feromona que hay entre ambas ciudades, premiando las rutas más olorosas. El programador debe ejustar la importancia relativa de estos dos aspectos con sendos parámetros. El nivel de olor no es sino un valor asociado a cada par de ciudades, que se ve incrementado cada vez que es elegido por una hormiga, y se ve decrementado en cierto porcentaje para simular la volatilidad. En cada ciclo computacional las hormigas avanzan un paso, y al cabo de n ciclos similares, cada hormiga ha regresado a la ciudad de la que partió.

Y vuelta a empezar. Se irán consolidado rutas, se irán olvidando otras, y al final; tras un criterio de parada establecido tendremos una buena aproximación al recorrido mínimo. El criterio de parada puede ser que se llegue al número máximo definido de ciclos completos, o que todas las hormigas sigan el mismo camino. En este último caso queda claro que no vale la pena continuar: la convergencia del algoritmo es clara. Ni siquiera en este caso tenemos asegurado que el recorrido obtenido será el óptimo, pero habremos obtenido una buena aproximación en un tiempo razonable.

Este tipo de técnicas nació con la tesis doctoral de Marco Dorigo en 1992 (Ant colony system). Actualmente existe toda una batería de métodos basados en esta idea, que difieren en la forma de actualizar el nivel de feromonas en cada tramo, principalmente. Dado que cada hormiga actúa con independencia (relativa) de las demás, se trata de computación en paralelo, y existen varias formas de paralelización; síncrona y parcialmente asíncrona.

Teneis una buena introducción a estos métodos en esta dirección

Los primos de Mersenne y los números perfectos.

Es bastante habitual encontrarse con reseñas científicas en las que se explica que se acaba de encontrar el mayor número primo conocido. Se suele tratar de un número expresable como una enorme potencia de dos menos una unidad. ¿Es que todos los primos grandes son de esta forma?

Vamos a comentar por encima la fascinante historia de los primos de Mersenne y su asociación con los números perfectos.

Un primo de Mersenne es un número primo expresable de la forma arriba citada. Ni todos los primos tienen esa forma ni todos los números de esta forma son primos. ¿Qué importancia tienen entonces son primos de Mersenne? Pues matemáticamente son los protagonistas de una apasionante historia que se mezcla con la de los llamados números perfectos . Pasamos a reseñarla.

Un número se denomina perfecto cuando es igual a la suma de sus divisores propios (exceptuando al propio número, que también es divisor de sí mismo). Así, el 28 es perfecto, pues sus divisores propios son 1,2,4,7 y 14; y suman precisamente 28
Después del 28, no aparece ningún número perfecto hasta el 496, el cuarto número perfecto es el 8.128, el quinto perfecto es 33.550.336. Se observa que cada número perfecto es mucho mayor que el anterior.El problema de encontrar estos números fue propuesto por Mersenne en una carta a Descartes.

La conexión entre los primos de Mersenne y los números perfectos era conocida desde muy antiguo: Euclides descubrió la fórmula para obtener números perfectos. Se trata de la fórmula que encabeza este artículo. Así pues, el número encerrado entre paréntesis es un primo de Mersenne. Encontrado uno de estos, tenemos irremisiblemente un nuevo número perfecto.

Euclides demostró que todos los números proporcionados por esta fórmula eran perfectos si el paréntesis era un primo de Mersenne, pero no se sabía si había números perfectos de otra índole. Dicho de otra manera: no se sabía si podían existir números perfectos que obedecieran a “otras fórmulas”. Esta situación cambió con Euler , que demostró que un número par es perfecto si Y SOLO SI se puede expresar de esta forma, con el paréntesis primo. Una condición suficiente y necesaria es lo más que puede pedir un matemático: es una caracterización. Así pues, en esta fórmula se encontraba todo el misterio de los perfectos, y de los primos de Mersenne.

Todo el misterio? Todo no, ni mucho menos. Euler demostró la caracterización de todos los números perfectos pares; pero no pudo conseguir ninguna caracterización de los números perfectos impares. Hoy no se conoce ningún número perfecto impar, pero nadie ha demostrado que no existan. De hecho, se sabe que en caso de existir debieran cumplir ciertas propiedades; propiedades que en todo caso son insuficientes para encontrarlos.

Tampoco se sabe si el número de primos de Mersenne es finito o infinito , y por lo tanto el de números perfectos. A la fecha de hoy el mayor primo de Mersenne conocido es dos elevado a 13466917 menos 1. Haría falta un grueso libro para escribirlo, pues tiene 4053946 cifras, y el perfecto asociado tiene 8107892 cifras.Hace falta un volumen de más de dos mil páginas para escribir este último número, a cincuenta renglones por página y 80 dígitos por renglón.

La forma utilizada hoy en día para encontrar primos de Mersenne y perfectos es el llamado teste de Lucas- Lehmer que dice que para p impar, el número de Mersenne asociado es primo (es un primo de Mersenne) si y solo si divide a S(p-1), siendo S una función definida recursivamente como sigue:

S(n+1) = S(n).S(n) -2,
S(1) = 4.

Existe un plan para encontrar primos de Mersenne mediante computación distribuida por PC’s particulares, al igual que el proyecto SETI . (The Great Internet Mersenne Prime Search GIMPS) La dirección del proyecto es esta.

Y una página muy interesante sobre dichos números está aquí.