Confundir media y mediana, ¿es una moda?
Una de las formas más inconvenientes de buscar información fidedigna es buscarlo en internet. En otra historia comentábamos que dado que en el desarrollo decimal de pi está TODO, es lo mismo que decir que no hay nada. Nuestra querida web, en la que tantas horas metemos pone a nuestra disposición una parte importante de totalidad del saber humano, así como una gran parte de la imbecilidad humana. Al faltar un criterio de decisión fidedigno, estamos perdidos. Me gustaría poder decir que lo que ustedes lean aquí es básicamente correcto y honradamente escrito, pero al fin y al cabo, ustedes me encontraron en la calle. No se crean nada de lo que pone aquí, ni en ningún otro ciberlugar. Al menos, mantengan activa la hipótesis nula de que la web no es un buen lugar para buscar la verdad, sobre todo si no saben quién la ha escrito. Estaría bien recordar que hace muy pocos años; allá por la prehistoria, los escritos no firmados eran simplemente ignorados...Todo esto viene a cuento de una frase que leí una vez en mi impulsivo navegar, y no he sido capaz de contrastar, ni de volver a encontrar. Esta frase me da pie a un artículo para el blog, así que lo contaré igual. No importa que sea cierta o no porque mil veces ocurren anumerismos similares, y lo importante es la reflexión subsiguiente, no la veracidad de la anécdota. Por lo tanto no mencionaré el país, ni el presidente concreto al que se atribuía la frase, que era más o menos esta:
El presidente se ha mostrado muy consternado al comprobar el resultado de una estadística fiable, según la cual la mitad de los ciudadanos tiene una inteligencia por debajo de la media.
No soy capaz de recordar si era inteligencia, nivel cultural u otra cosa similar, en todo caso era una cualidad positiva la que se estaba midiendo.
El resto de la noticia era una mofa hacia el compungido presidente, que se podía resumir así: ¡Qué burro el presidente, no sabe que por definición de la media, eso debe ocurrir necesariamente!
Es una confusión muy común. Además socialmente es muy excusable. Hoy en día es incluso de buen tono exhibir ignorancia en cuestión de números, y no digamos de estadísticas. En sin embargo ahí donde nos engañan todos los días. El anumerismo (de los demás, claro está) es una de las mejores herramientas de manipulación.
En el caso que nos ocupa, a mi no me queda claro que la estulticia presidencial estuviera por encima de la media, ni que la del comentarista estuviera por debajo.
Para empezar, debiera comentar que la intuición no es una herramienta de fiar en matemáticas. Es tan importante como la inspiración en los poetas, pero no más. No creo que con inspiración se pueda componer una gran obra, sino con mucho trabajo y sudor. Posiblemente el presidente caía en un error, pero el comentarista caía en otro con total certeza. Vamos a explicarlo.
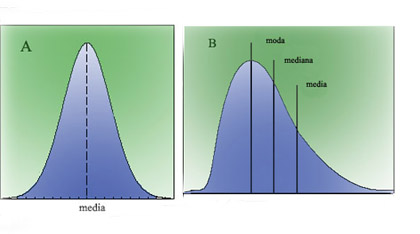
Debido a una cosa muy interesante y muy profunda de la que me gustaría hablar otro día y que se llama el Teorema central del límite , estamos acostumbrados a las distribuciones simétricas, como la de la figura A. En ellas coincide la media ( que todo el mundo sabe lo que es), la moda (que es el valor con mayor frecuencia observado) y la mediana, que es el valor que deja tantas observaciones por arriba como por debajo. Si la distribución no es simétrica, tenemos situaciones como la de la figura B. La media está desplazada respecto a las demás medidas centrales, y es claro que en este segundo caso más de la mitad de la población está por debajo de la media. Siempre será la mediana, por su propia definición la que estará centrada respecto al número de observaciones a ambos lados, no la media.
¿Tenía nuestro hipotético presidente motivos de pesar?
Pues según se mire, sí. Si la distribución hubiera sido asimétrica en sentido contrario a la de la figura B, más de la mitad de la población hubiera tenido una inteligencia, cultura o educación superior a la media, puesto que la mediana sería de valor superior a la media. Esto supone un desplazamiento de la masa total hacia valores más altos, y es claramente positivo para la población, si el parámetro que se mide es una cualidad positiva para la misma. Eso no se producía, pues la noticia implicaba una distribución simétrica.
¿Se refería a eso el presidente? Lo dudo.
¿Tenía motivos de mofa el comentarista? Pues realmente, si los tenía no era por lo que él creía...
12 comentarios
maria -
isbelia -
°_° Tu -
asgard -
Te hubiera enviado un mail pero no he encontrado datos de contacto ;)
Un saludo,
Asgard
margarita -
Profe -
nataly fuentes garcia -
BERENICE MAÑON MORENO -
Luiz -
luis -
alejandra -
Chewie -