Intuiciones y mentiras.
 Una constante en este blog será la insistencia en que la intuición por sí sola no es una buena guía en matemáticas. Afortunadamente, tenemos una herramienta que nos sirve de brújula: el razonamiento riguroso. Lo que sigue es una muestra de los errores de la intuición, que son siempre debidos a dar por sentado cosas que no son ciertas; quizás porque tenemos una tendencia mental a extrapolar nuestras vivencias diarias a lugares en los que las cosas son ligeramente más complicadas.
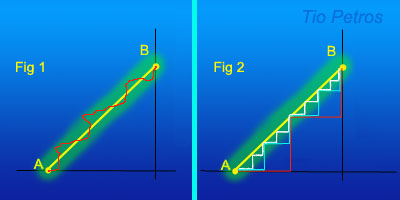
Una constante en este blog será la insistencia en que la intuición por sí sola no es una buena guía en matemáticas. Afortunadamente, tenemos una herramienta que nos sirve de brújula: el razonamiento riguroso. Lo que sigue es una muestra de los errores de la intuición, que son siempre debidos a dar por sentado cosas que no son ciertas; quizás porque tenemos una tendencia mental a extrapolar nuestras vivencias diarias a lugares en los que las cosas son ligeramente más complicadas.Miren ustedes la figura 1. Tenemos una recta que une los puntos A y B, cuya longitud es raíz de 2, en virtud del teorema de Pitágoras. Imaginen una banda de espesor e centrada en la recta AB. Consideremos todos los posibles caminos de A a B, completamente en el interior de la banda, que no tengan retrocesos. Unos serán más largos que otros, y el camino recto será, lógicamente el más corto. El que aparece en rojo en la figura es uno de los posibles.
Razonemos con sentido común:
Si vamos disminuyendo el espesor e de la banda, vamos obteniendo caminos cada vez más cercanos a la recta. Si el espesor de la banda tiende a cero, los caminos tenderán a la recta, y la longitud de los mismos tenderá a raíz de 2.
Podemos entonces enunciar la siguiente conjetura:
La longitud del camino más largo de A a B en el interior de una banda de espesor e centrada en la recta AB tiende a la longitud AB cuando el espesor de la banda tiende a cero.
¿Existe algo más lógico, coherente con nuestra experiencia cotidiana y racionalmente satisfactorio?
Pues bien, todo es mentira. Lo anterior es una llamada a la buena voluntad y al sentido común del futuro creyente en la conjetura, no una demostración. Y en matemáticas esto no sirve.
De hecho, existen caminos de longitud exactamente 2, mucho mayor que la distancia AB para cualquier espesor de la banda. Esto parece una afirmación extraordinaria, y en parte lo es pues parece contradecir el sentido común.
Afirmaciones extraordinarias requieren pruebas extraordinarias .
¿Con qué tipo de prueba podría un matemático avalar esta afirmación? Demostrar la falsedad de una conjetura admite dos estrategias: demostrar desde la generalidad que si fuera cierta, se caería en una contradicción (reducción al absurdo) o poner un contraejemplo.
Haremos lo segundo. Fíjense en la figura 2.
Tenemos una camino de A a B que va en horizontal hasta el origen y sube verticalmente hasta B, de longitud 2. Podemos complicar este camino añadiendo escalones intermedios, como se ve en color rojo , verde y blanco. Si repetimos este proceso, obtenemos caminos de A a B, todos ellos de la misma longitud 2. Por pequeño que sea el espesor de la banda, siempre podremos hacer que todo el camino esté dentro de ella. En el límite, a pesar de tener un camino infinitamente próximo a la recta AB, no es cierto que este camino comparta las propiedades de la recta: sigue siendo de longitud 2. Es una curva con infinitos puntos de no derivabilidad que nada tiene que ver con una recta, a pesar de su infinita proximidad.
La existencia de estas funciones "patológicas" tiene un puesto de honor en la historia de la matemática, y da paso al tópico por excelencia de la última década en matemáticas: los fractales.
_________________________________________________________________________________________________
El estudio de las funciones entre dos puntos dados que cumplen determinadas propiedades dio paso a la revolucionaria idea de espacios matemáticos en los que sus puntos no son los puntos del espacio, sino las propias funciones. Así nació el cálculo funcional, en el que se manejan espacios de infinitas dimensiones, fecundo campo de investigación matemático a lo largo de todo el siglo XX, cuyo origen podemos datar en los mismos nacimientos del análisis. Banach y Hilbert sentaron las bases modernas de los espacios normados y métricos generales, y hoy en día plantean multitud de problemas analíticos y sobre todo topológicos pendientes de resolver.
4 comentarios
Adolfo -
AM -
Tio Petros -
Un saludo.
PD.Yo también creo que el entrenamiento matemático te cambia la intuición con estas cosas.Ya se sabe: cuando uno ha caído ya muchas veces en la misma piedra... espabila-
[Quique] -