Ramsey y grafos
Los últimos post del mes de Febrero trataban de explicar el enunciado (que no la demostración) del Teorema de Ramsey . Comentamos entonces que dedicaríamos varios comentarios a aplicaciones prácticas del mismo, para acabar de comprender el sentido profundo del teorema. Para ello, vamos a apoyarnos en la teoría elemental de grafos. Un grafo no es más que una colección de puntos, junto con aristas que unen unos puntos a otros. Vamos a restringirnos a grafos simples no orientados, en los cuales los lazos entre puntos no tienen dirección, y no existen lazos múltiples entre la misma pareja de puntos; ni lazos que vayan de un punto al mismo punto. Cada arista por tanto une dos puntos, y es una buena representacione de una relación entre los mismos.
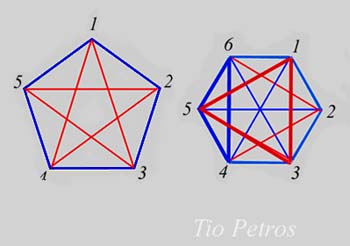
Un grafo es completo cuando toda pareja de puntos tiene una arista que los une. El grafo completo de n vértices se denomina Kn. En la figura tenemos dos grafos completos: K5 y K6. Sus aristas han sido coloreadas de dos colores: rojo y azul.
Veamos el siguiente enunciado:
En un grupo de seis personas, o se cumple que tres se conocen entre sí, o se cumple que tres no se conocen entre sí
En las figuras, cada persona del grupo es un punto, y las aristas representan la relación de conocimiento o desconocimiento mutuo entre ellos. Digamos que rojo indica que sí se conocen y azul lo contrario.
Una alternativa al enunciado anterior es la siguiente:
Si en un grafo completo K6 coloreamos sus aristas de dos colores, siempre encontraremos un subgrafo K3 monocolor.
Espero que sea evidente para el lector la equivalencia entre ambos enunciados, y espero también que aprecie el "sabor a Ramsey" de este último.
En efecto, tenemos una aplicación directa del teorema de Ramsey: tenemos un conjunto X de seis puntos; tenemos el conjunto de todos sus subconjuntos de dos elementos (R=2), que no son sino las aristas del grafo , y coloreamos todas ellas usando dos colores. Ahora, dados los números tres y tres , el teorema de Ramsey nos asegura que si el conjunto X es suficientemente grande, existirá en su seno un conjunto de tres puntos unidos tan sólo por aristas de color rojo, o un conjunto de tres puntos unidos tan sólo por aristas de color azul.
Las figuras nos demuestran que para el caso de cinco personas, no es obligado el cumplimiento. Es muy fácil demostrar que con seis sí. En el caso concreto que presento, aparecen regruesados dos subrafos de orden tres monocromáticos: los que tiene como vértices (1,3,5) rojo; y los que tienen como vértices (4,5,6) azul.
El Teorema de Ramsey nos dice que si el número es suficientemente grande, en un grupo habrá, por ejemplo 20 personas que se conozcan entre sí dos a dos, o 15 personas que no se conozcan mutuamente. Para cualquier par de números, existirá un número mínimo R(m,n;2) por encima del cual, un conjunto de personas tendrá en su seno m personas que se conozcan todas ellas dos a dos, y n personas que no se conozcan. R(3,3;2) = 6, como acabamos de ver. En general, los valores de los números de Ramsey son desconocidos; pero hablaremos de ello en próximos días.
Volvemos a poner el enunciado para animarles a releerlo. Seguramente ya no parece tan extraño como hace unos días...
2 comentarios
Tadalafil -
blabla -
CHAO