Cosas de los espacios infinitodimensionales
Nos es imposible visualizar un espacio de más de tres dimensiones, y sin embargo no tenemos ningún problema para trabajar con espacios de más dimensiones. Muchas veces, la extrapolación a mayor número de dimensiones es tan trivial, que en los libros de texto se omiten los detalles...La cosa cambia sin embargo de forma drástica cuando el número de dimensiones es infinito.
Vamos a comentar una aspeto curioso y sorprendente de dos cuerpos infinitodimensionales: la esfera y el cubo.
No nuestra esfera ni nuestro cubo (hexaedro), ciertamente, sino el equivalente en espacios de dimensiones cada vez mayores, hasta llegar al infinito numerable.
Una esfera se define en cualquier espacio como el conjunto de puntos que equidistan de otro dado. Pasaremos por alto el "detalle" de que debemos tener definida una distancia entre cada pareja de puntos, y supondremos que estamos hablando de la distancia euclídea normal; esa que todos conocemos.
En dos dimensiones tenemos círculo, que es una superficie plana. En tres, tenemos la esfera de toda la vida; una superficie cerrada en forma de balón. Para treinta y cinco dimensiones, la definición es la misma; a pesar de que seamos incapaces de visualizar el objeto.
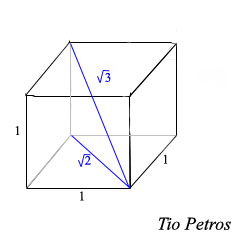
Un cubo unidad lo podemos definir como el conjunto de puntos generados por vectores unitarios de una base ortonormal del espacio, mediante combinaciones lineales en las que los coeficientes van de cero a uno. Este galimatías no quiere decir otra cosa que lo que todos ustedes saben: dado un punto de origen, que será uno de los vértices del cubo, dibujamos tantas flechitas perpendiculares entre sí como dimensiones tengamos, y ya tenemos las aristas del cubo que convergen en ese vértice... lo demás es dibujo lineal.
Pues bien: ¿Cuál es la longitud del mayor segmento que cabe dentro de un cubo y dentro de una esfera?
Para una esfera, es evidente que el mayor segmento pasa por el centro, y tendrá una longitud de dos veces el radio. Eso sucede con la esfera de en un espacio de dos dimensiones(círculo), y con la esfera en un espacio de tres (nuestra esfera de toda la vida). Por la propia definición de esfera, no importa la dimensión del espacio, del centro a cualquiera de sus puntos la distancia es constante e igual al radio, y el mayor segmento que cabe en el interior es un diámetro, de longitud doble al radio.
¿Y qué sucede con el cubo?
Pues la sorpresa es que el cuadrado, el cubo y las demás figuras correspondientes a máyores dimensiones tienen diagonales, cuyas longitudes son mayores que los lados. Para el cuadrado, la diagonal vale raiz de dos, y para el cubo vale raíz de tres. Una diagonal en un hipercubo n-dimensional mide raíz de n, que es una función creciente de n, y por lo tanto, en un espacio de infinitas dimensiones dentro de un cubo cerrado CABE UNA RECTA INFINITA.
8 comentarios
La cruz -
el Menex -
el cojo -
ToReK -
Shunt -
He leido que todo el universo podría ser un simple punto en un espacio de infinitas dimensiones pero no sé si tiene mucho que ver.
Carlos -
Crystal -
rimblow -