El calendario (4)

Hemos comentado en posts anteriores que el concepto de congruencia era imprescindible en este estudio, vayamos con él:

CONGRUENCIAS

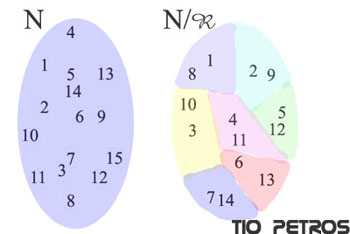
Supongamos que tenemos el conjunto N de todos los números naturales. Tomemos un natural cualquiera, por ejemplo el siete. Cuando dividimos por siete, el resto de la operación es un número comprendido entre 0 y 6. Pues bien, vamos a asociar a cada número natural el resto de su división por siete. Y ahora agrupamos los naturales en siete compartimentos; según los restos de la división realizada.

Esto que hemos hecho es establecer una relación de equivalencia (reflexiva, simétrica y transitiva). Todo número da el mismo resto al dividir por siete que sí mismo, si a da el mismo resto que b , entonces b lo dará igual que a , y si a da el mismo resto que b , y b da el mismo resto que c , entonces a dará el mismo resto que c . Cuando una relación tiene estas tres propiedades, se denomina de equivalencia, y cristaliza el conjunto original en una serie de compartimentos estancos dentro de cada uno de los cuales están todos los elementos relacionados entre sí, y solamente entre sí.

Estos compartimentos se denominan clases de equivalencia, en nuestro caso clases de restos módulo 7 , y clases de restos módulo p en el caso general. El conjunto de las siete clases se denomina conjunto cociente por la relación dada, y es un conjunto con p elementos(7 en el ejemplo que nos ocupa) , cada uno de los cuales es una clase, cada una de las cuales tiene dentro los elementos originales. Dicho conjunto cociente se denota N/R, siendo R la relación de equivalencia que hace cristalizar el conjunto original en clases, y en nuestro ejemplo concreto, se denominará N/p: conjunto cociente de clases de resto módulo p. Cada clase se expresa poniendo entre corchetes uno cualquiera de sus elementos; así en nuestro conjunto cociente de restos módulo 7, se cumple que [1]=[8]; la clase del 1 y la del 8 son la misma (lo cual es normal, dado que el 1 y el 8 son congruentes módulo 7.

Dos elementos que pertenecen a la misma clase, se denominan congruentes módulo p. En nuestro caso, vemos que el 9 y el 2 son congruentes módulo 7. Los números 16, 23,30, 37,...(7k+2),... también son congruentes módulo 7 con el 2 y el 9. Efectivamente, todos ellos dan un resto de 2 al dividir por 7. Cada clase de restos módulo p es representada por uno de sus elementos, normalmente el más pequeño, que se denomina el representante canónico de la clase. Así, el 1 es el representante de la clase [1],

La frase Los números a y b son congruentes módulo p se escribe de la siguiente manera:



Aunque en sentido estricto no lo son, podemos trabajar con las congruencias como si de ecuaciones se tratara, e incluso podemos formar sistemas de congruencias, de esta forma:



El teorema chino del resto nos da las pautas para saber cuándo un sistema de este tipo tiene solución. En efecto, aunque estamos acostumbrados a decir que un sistema de n incógnitas necesita n ecuaciones para tener solución, las cosas son más complicadas. El Teorema de Rouché-Frobenius da las condiciones suficientes y necesarias para que tal cosa ocurra, pero de ello ya hablaremos en otra ocasión. Baste decir que el teorema chino del resto nos dice que un sistema de congruencias como el anterior tiene solución si los módulos p ₁, p ₂,..., p _n son primos entre sí dos a dos. Esto quiere decir que tomando dos de ellos cualesquiera, no existe ningún número que divida exactamente a ambos, salvo la unidad.

Cuando esto ocurre, el sistema tiene solución única módulp p ₁x p ₂x...x p _n.

Si lo piensan un poco, esto es lo esperable. Pero si no les apetece pensarlo, hablaremos de ello en otro momento.

Por ahora, el lector se preguntará qué relación tiene esto con los días julianos.

Pues bien: hemos dicho que Scaliger quería encontrar un origen para su sistema; un año x en el pasado que fuera a la vez inicio de los tres ciclos.

Scaliger sabía que el año 1.560 tenía 1 como número del ciclo solar. También sabía que el año 532 fue el que Dionisio el Exiguo introdujo el sistema del ciclo lunar, y que tenía dicho año número áureo igual a 1. Sabía asimismo que el ciclo fiscal de indicción romana se instituyó el año 313 por Constantino, con lo que dicho año tenía número 1 en su correspondiente ciclo.

Los tres ciclos tienen módulos 28,19 y 15 respectivamente, luego el año inicial buscado deberá ser congruente con las tres fechas citadas vía sus respectivos módulo(pues cada uno de ellos era el primero de su correspondiente ciclo). Esto es:



Simplificamos este sistema: lo explico para la primera congruencia: 1560 es congruente módulo 28 con muchos números. Si los ordenamos todos, veremos que están separados 28 unidades cada uno del siguiente, porque estamos trabajando en módulo 28. Se trata de encontrar el más bajo congruente con 1560. Esto se hace buscando el múltiplo de 28 más cercano a 1560 por debajo, que es 55x28=1540. Como nos faltan 20 para llegar a nuestro 1560, resulta que 20 es el número buscado, congruente con 1.560 módulo 28. Luego podemos sustituir 1560 por 20 en la primera congruencia, sin variar el contenido de la misma.


Espero que el lector se de cuenta de que esta simplificación no es otra cosa que sustituir los números 1560,532 y 313 por los representantes canónicos de sus clases respectivas.

En definitiva, obtenemos:



Tenemos suerte: los tres módulos son primos entre sí por parejas, luego el Teorema Chino del resto es de aplicación:

Lo haremos pormenorizadamente en el próximo post, que será un mero desarrollo de los cálculos, por aquello de que lo hemos prometido. Así pues, el siguiente post sólo tendrá interés para los que quieran llegar hasta el final; el resto, simplemente puede obviarlo.