Los números de Catalán
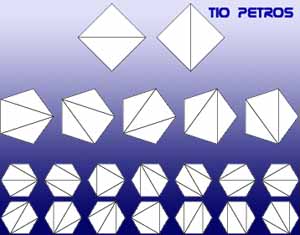
La combinatoria es una de las ramas más arduas de la matemática (al menos desde mi humilde entender). No es otra cosa que el arte (o la técnica) de contar. Conforme se va complicando lo que queremos contar, es lógico que se vaya complicando proporcionalmente la forma de contarlo. Sin embargo, a veces la complicación es muy grande cuando lo que contamos no es tampoco nada del otro mundo. Me explico: en este momento tratamos de contar triangulaciones de polígonos, que supondremos regulares, o al menos convexos.Una triangulación de un polígono es una partición del mismo en triángulos disjuntos cuyos vértices coinciden con los vértices del polígono. En la figura pueden ver todas las posibles triangulaciones de un cuadrado, un pentágono y un hexágono. Denominaremos C n al número de posibles triangulaciones diferentes de un polígono utilizando n triángulos.
Si el polígono en cuestión tiene m lados, necesitaremos m-2 triángulos para hacerlo. En efecto, es fácil convencerse de esto comprobando que sólo dos de los triángulos comparten dos lados con el polígono, y todos los demás comparten necesariamente un lado tan sólo. Por tanto, C n denotará tanto el número de triangulaciones de un polígono para el que se necesitan n triángulos, como el número de triangulaciones de un polígono de un polígono de n-2 lados.
En la figura se muestra que C 2=2; C 3=5 y C 4=14.
El lector puede intuir que el procedimiento de contar exhaustivamente todas las triangulaciones deja de ser factible enseguida: debemos encontrar atajos, y en la búsqueda de atajos es donde se expresa el genio matemático, porque contar de uno en uno lo sabemos hacer todos, y no tiene gracia alguna.
Estudiaremos la recursividad de la sucesión de Catalán C 0, C 1, C 2,...en la que obviamente C 1=1, C 2=2, y haremos C 0=1.
Este método de encontrar los valores de C n basándonos en valores anteriores, que se consideran ya conocidos es el método de recurrencia que ya explicamos en su día.
El conocimiento de la fórmula de recurrencia de una sucesión no nos ofrece simplemente la posibilidad de encontrar más fácilmente los elementos de la sucesión: también nos dice muchas cosas más. Por ejemplo: si demostramos que varios problemas de conteo, aparentemente dispares obedecen a la misma ley de recurrencia, hemos demostrado que en ambos problemas subyace el mismo concepto matemático. En el caso que nos ocupa, el de los números de Catalán (1), se han encontrado hasta 66 problemas geométricos de conteo accesibles mediante dichos números.
Lo vemos en el siguiente post.
____________________________________________________________________
Así denominados en honor a Eugene Catalán (1814,1894), matemático belga.
3 comentarios
ary -
n es 4 para el hexagono no¿?
Me encanta tu web
p.d: viva Euler y los Bernoulli!
TioPetros -
juan -
cada dia me sorprendes mas, tio petros.
lo unico que se respecto a triangulaciones es su relacion con la topologia de superficies, pero este nuevo enfoque seguro que es excelente.
espero con ansia la ley de recurrencia. hay que ver que fantasticas y sorprendentes son a veces las matematicas que nos dan estos ejemplos tan enigmaticos.