Blogia
Tio Petros

Recurrencia de Catalán

- Conceptos
Recurrencia de Catalán Vamos a obtener la fórmula de recurrencia de los números de Catalán. Para ello, fijemos la nomenclatura: Cn es el número de triangulaciones con n triángulos, o lo que es lo mismo, de un polígono convexo de n+2 lados. Visto de otra forma: un polígono con i lados tendrá Ci-2 triangulaciones posibles.

Dado que el mínimo polígono existente tiene 3 lados, y se trata del triángulo, con una única triangulación (valga la redundancia y nunca mejor dicho), tenemos que C1=1. Haremos C0=1, como caso inicial.

Supongamos conocidos los valores de los primeros Cn.Intentaremos hallar Cn+1. Esto equivale a suponer conocidas las triangulaciones de polígonos hasta (n+2) lados e intentar conocer las del polígono de (n+3) lados.

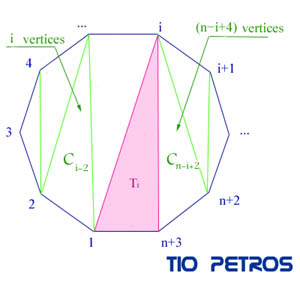
Sea P un polígono de (n+3) lados, que numeraremos 1,2,3,…,n+2,n+3. Elegimos uno de los lados, el que tiene como vértices {1,(n+3)}. Una vez elegido este lado, tomamos uno de los vértices restantes (que llamaremos vértice i ) para formar un triángulo. (En rosa, el triángulo Ti en la figura). Dicho triángulo divide al polígono P en tres partes: un subpolígono P1de vértices {1,2,3,…,i}; el propio triángulo Ti y otro subpolígono P2 de vértices {i,i+1,i+2,…n+2,n+3}.

P1 tiene obviamente i vértices. P2 tiene (n-i+4) vértices. Esto quizás no es tan fácil de ver. Se comprende mejor al ver que la suma de los vértices de P1 y P2 debe ser una unidad superior a los vértices de P, puesto que el vértice i lo tomamos dos veces, una para cada subpolígono. Así pues deben sumar entre ambos (n+4) vértices, y por lo tanto P2 tendrá (n-i+4) vértices.

Sabiendo el número de vértices de P1 y P2, sabemos automáticamente sus respectivos números de triangulaciones: Ci-2 y Cn-i+2 respectivamente. Luego para el triángulo Ti escogido tenemos Ci-2 .Cn-i+2 posibles triangulaciones.

Resulta que el vértice i lo podemos elegir desde i=2 hasta i=(n+2) para formar el triángulo Ti, luego tendremos tenemos que las posibles triangulaciones del polígono P, de (n+3) lados será dicho producto Ci-2 .Cn-i+2 extendido a todos los posibles valores de i:

Esto es:

Cn+1=C0 Cn+ C1 Cn-1+ C2 Cn-2+…+ Cn-2 C2+ Cn-1 C1+ Cn C0

Que es la fórmula de recurrencia deseada.

Dado que conocíamos los primeros casos:

C0=1
C1=1
C2=2 triangulaciones de un cuadrado

Ahora podemos fácilmente ir hallando los siguientes:

C3=1.2+1.1+2.1=5 triangulaciones de un pentágono
C4=1.5+1.2+2.1+5.1=14 triangulaciones de un hexágono,… etc.

10 comentarios

TioPetros -

:)

juan -

gracias, ya puedo ver los archivos hasta ahora prohibidos para mi!!!!!!!!!!!!!!!!!

TioPetros -

Me alegro que te haya gustado, JuanPablo. Respecto a la pregunta de Juan, creo que la respuesta de JuanPablo es la más acertada. Buscando en el oráculo (google, claro) "GhostView" podrán bajarte un programita para visualizar los archivos de extesión .ps, y buscando "DVIscope" te podrásn bajar el correspondiente para los archivos de tipo .dvi
Junto con los .pdf de Acrobat reader, creo que son los tres formatos en los que se encuentra casi todo en la web.

JuanPablo -

TioPetros, excelente el link!

El post también, pero ahora me quedé pensando en el tablerito de ajedrez... Cómo habrán llegado a ese problema?

JuanPablo -

juan, en latex no pueden 'verse' las fórmulas

(claro, con entrenamiento uno reconoce que $C_{n+1} = C_n + ldots $ es Cn+1 = Cn + ... , pero cuesta).

Tendrías que bajar un compilador, que cree un archivo dvi, ps o pdf (el mejor, para mi, es el MikTex, y como procesador del texto, el WinEdt, o el TexNicCenter (buscando en google, aparecen las páginas de donde descargarlos).

Para ver un archivo ps, sólo hace falta instalar un programita como el GhostView (otra vez, es mas fácil que lo busques por google, es gratuito, y ahí vas a tener las instrucciones para instalarlo).

juan -

muchas gracias, tio petros, pero me temo que aun soy lego en materia de articulos cientificos digitales. como abro ese archivo? y ya de paso otra pregunta, existe algun visualizador de archivos de latex que realmente funcione? aun no he encontrado ninguno.

TioPetros -

Hola Juan.
En la siguiente dirección:
http://www-math.mit.edu/~rstan/ec/catalan.ps.gz
tienes 66 interpretaciones geométricas de los números de Catalán, que corresponden a 66 situaciones en las que dichos números aparecen para contabilizar disposiciones geométricas.
(El archivo está en formato Post_Script)

TioPetros -

Hola Jorge. C0=1, no por un capricho,, y no se toma dicho valor en base a la función de recurrencia, sino antes. Verás: si has seguido el método para encontrar la función de recurrencia, habr´ñas visto que el vértice móvil "i" va tomando valores desde 2 hasta (n+2).
En los casos extremos, para i=2 y para i=n+2, no tenemos la división del polígono inicial en tres partes; dos subpolígonos y el triángulo Ti, según habíamos visto.
Tenemos sólo dos partes: el triángulo Ti y el resto del polígono. Para dicho caso,el número de triangulaciones posibles (con Ti fijo, claro está) es simplemente el número de triangulaciones del resto del polígono. Llamando CO a las "triangulaciones" del otro polígono (inexistente en estos casos extremos), y haciendo C0=1, podemos incluir dichos casos extremos en la fórmula de recurrencia respetando la factura de los demás casos, para compactificar la fórmula. Se trata de una arbitrariedad convenida en aras de la claridad. No obstante, si lo prefieres, podemos no suponer valor alguna para C0, y expresar la fórmaula de recurrencia así:
Cn+1=Cn+C1Cn-1+...+C1Cn-1+Cn.
Sin expresar los dos sumandos extremos como productos, sino simplemente como Cn.
A mi me parece más redonda la fórmula con C0; pero ya tre digo, no aporta "substancia matemática" al asunto...

Jorge -

"Haremos C0=1, como caso inicial." ¿Y por qué no otro valor?

Está claro que se toma ese valor en base a la función de recurrencia, y no antes.

juan -

fantastico, sencillamente fantastico.
es una deduccion que me parece muy interesante. alguna aplicacio a algun roblema concreto de los numeros de catalan? no es que sea necesaria, su belleza no necesita de necesidad.