Blogia
Tio Petros

Continuidad

- Conceptos
Continuidad
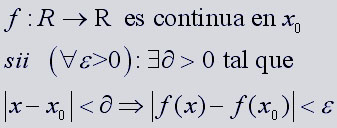
La ciencia se puede aprender de memoria, pero la sabiduría no.

Laurence Sterne
(1713-1768) Novelista británico

Miren la ilustración que encabeza el post.

Este galimatías suele ser el primer encuentro de un estudiante de bachiller (o como lo quieran llamar ahora, porque sólo los profesionales del ramo saben cómo coño se denominan en cada momento los estudios que cursan los adolescentes)...decía que este aparente galimatías suele ser el primer encuentro de un chaval con la matemática de verdad.

Dicho encuentro es invariablemente traumático. Y la verdad es que parece mentira que tras estas cadenas de símbolos se encuentre tanta sutileza, tanta belleza y tanta historia.

No es por casualidad que hablamos de ello ahora. Si el lector ha seguido los últimos post, aunque nada supiera del tema tiene las herramientas conceptuales necesarias para hacer muchas cosas interesantes.

Como en otras ocasiones, detrás de estos símbolos están ideas topológicas mucho más profundas que las que sospechan los estudiantes de BUP.

El hecho de que tantos estudiantes se hayan estrellado contra estos dos renglones, poniendo ojos como platos y decidiendo aprenderlos de memoria, como única alternativa a la locura es doblemente penoso. Por un lado, todas las grandes ideas son muy sencillas, y esta también lo es; por otro lado, sin entender BIEN esto, poco análisis matemático se puede comprender realmente. Y créanme que sé de lo que hablo: durante años estuve dando clases particulares a chavales y bien raro era encontrarse con alguno que supiera exactamente qué significaba todo esto.

Esta definición es la superación de la fase intuitiva en el cálculo. La mayoría de edad de la matemática, debida a inmensos cerebros que se llamaron Cauchy, Weierstrass, y un largo etcétera. Es una expresión estática, sin frases vagas del tipo " cuando la x tiende a tal cosa" o " cuando tal distancia se hace infinitamente pequeña ". Es estática como estático es un cristal natural perfecto o una obra de arte escultórica.

Como es tan importante, y no tenemos prisa, le dedicaremos varios post. Al final, nos parecerá tan clara como si estuviera escrita en castellano; y si no es así, será exclusivamente por mi culpa.

Hasta la semana que viene.

18 comentarios

Jordan 11 -

Time cures sorrows and squabbles because we all change, and are no longer the same persons. Neither the offender nor the offended is the same.

jose -

La primera definición que yo vi con existes, para todo's y epsilones fue la de límite de una sucesión. Al principio te desesperas pero al coger costumbre te das cuenta de que definir cosas con palabras normales es mucho más difícil que hacerlo con la notación si no quieres perder precisión. Es como aprender a usar LaTeX (¿y qué creen que hago a esta hora precisamente?). Cuando te acostumbras te es imposible volver al editor de ecuaciones del Word.

TioPetros -

Sergi; efectivamente, a mi me gusta más explicar la continuidad sin la noción previa de límite. Creo que la definición por entornos (o la épsilon-delta; que es lo mismo) captura exactamente la idea de continuidad.

Sergi -

Tio Petros: Perdón por responder a tu comentario con tanto retraso. He estado "missing" unos días. Por supuesto, estoy de acuerdo con tu enfoque. El comentario iba más bién en la línea de que al meter primero el concepto de límite y después el de continuidad las cosas se hacen más enrevesadas.

Cluje -

Por cierto samu, lo de la aorta del análisis, sencillamente brillante!

Cluje -

Qué maravilla, Tío Petros, al final vas a contar la historia! :D Yo no sabía que te habías puesto manos a la obra tan pronto (llevo unos días sin poder bloguear), y he hablado un poquitín de este tema en el Lolaberinto y en el Musolari errante.

De todas maneras, me encanta conocer la historia y saber que la vas a contar tú. Es como cuando vas a ver una adaptación de Shakespeare hecha por Welles o Kurosawa: sabes que el sustrato es genial, y también que el director va a hacer otra (no la misma) maravillla con ella. Mmm el placer previo es el mejor...

samu -

Hicieron falta muchos siglos de historia para poder alcanzar una definicion tan depurada como esta.
Solo un detalle, esta definicion no es mas que un caso particular de otra mas general en la que se utilizan espacios metricos cualesquiera.
En mi caso solo al ver la definicion general pude comprender su verdadera magnitud.
Me atreveria a decir que esta definicion es la aorta del analisis. no podriamos vivir sin ella.

Palimp -

Recuerdo cuando leí está definición, me pareció curiosa. Sólo muchos años después supe que, como dice jezk con las palabras de Jardiel Poncela, eran fruto de mucho esfuerzo.
Es una pena que a los estudiantes se les planten las definiciones así, a bocajarro, sin explicar un poco de donde vienen y por qué son así. Supongo, ya que soy profesor y puedo entenderlo, que en primer lugar no hay tiempo, y en segundo que a los alumnos tampoco les interesaría. Pero se entendería mucho mejor.

jezk -

Frase de Enrique Jardiel Poncela, leída hoy mismo en un periódico local: "Lo que se lee sin esfuerzo ninguno, se ha escrito muchas veces con un gran esfuerzo".
Sólo tú sabrás, Tiopetros, todo el esfuerzo que pones en la redacción de tus artículos. Ya sólo por ello merecen una lectura más atenta. Gracias!.

Tiopetros -

Tranquilo, jezk. Ahora eres más sabio que hace media hora...

jezk -

Perdón, me he precipitado.
Acabo de descubrir la abreviatura de "si y sólo si".
Novatada!.

jezk -

Creo que hay alguna errata en la ilustración del post, no?
Respuesta: "sii..."

Akin -

Bueno, asistiré con interés. En su momento conseguí comprenderlo pero hace ya tanto... :)))

(Y sí, me parece precioso)

Carlos -

La verdad es que a mi me gusta más la noción de límite puramente topológica... pero vamos, que lo de aritmetizar el análisis fue todo un hito, pero lo de la topología, bueno, aún costó más tiempo llegar ...

juan -

una definicion de epsilon-delta?
hacia tiempo que no veia alguna...
siempre hace ilusion recordar estas cosas. vamos, tio petros, que tenemos que llegar hasta la homologia de las esferas...

TioPetros -

Sergi: creo que es mucho mejor, y parece que estás de acuerdo, plantear PRIMERO la idea de continuidad, sin hacer mención de límite alguno. De hecho, así lo voy a hacer.
Creo que es la forma natural de hacer las cosas.

Lola -

es más que cierto que algunos conceptos que se ven en 1º de carrera, que se aprueban en el examen, que sabemos hacer los ejercicios con los ojos cerrados.... se revelan ante uno más tarde. A mí me pasó con varias cosas, una de ella el concepto de límite, cierto. Otra las aplicaciones inyectivas, sobreyectivas y biyectivas y otra lo de pasar a cociente. Pero cuando las ves, mientras andas por calle aparecen y ¡¡¡plof!!! ¡¡claaaaaaro!!. Es maravilloso. Ejem... somos un poco incomprendidos con este sentido de belleza que tenemos, eso sí.

Sergi -

Solamente una precisión. Para acabar de desalentar a los pobres muchachos, el galimatías del principio de explica normalmente en dos etapas. Primero la enrevesada definición delta-epsilon de límite y a continuación la definición de continuidad a partir de la igualdad entre límite y valor de la función en ese punto. En cualquier caso, coincido plenamente con todas y cada una de las ideas del post. Es imposible que ningún adolescente sea capaz de intuir toda la belleza y profundidad de pensamiento que esta definición encierra cuando el único esfuerzo que realiza el docente para facilitar esa comprensión es dibujar una función claramente discontinua (con un salto finito, normalmente) y alguna idea del tipo "una función es continua si puedes dibujarla sin levantar el lápiz del papel".