¿Qué es una función medible?
Viene de aquí.
Vamos a fijar un poco la nomenclatura para entendernos. Hemos afirmado que la integral de Lebesgue es aplicable a un mayor número de funciones que la de Riemann. Este conjunto de funciones es el de las funciones medibles. Una función medible está definida en un espacio de medida, en el que "todos" los subconjuntos tienen asociado un número, que es la medida del mismo. La palabra todos aparece entrecomillada porque en realidad no son todos , sino un número muy grande de ellos, que forman una estructura denominada sigma-algebra de los conjuntos medibles del espacio dado. Una sigma-algebra no es sino una colección de subconjuntos tales que toda unión, intersección o paso al complementario así como uniones numerables de subconjuntos es un nuevo subconjunto que también de la misma pertenece a ella, .
Cuando estuvimos hablando de variables aleatorias mencionamos el concepto, que no vendrá mal recordar aquí. Allí venía a cuento porque los espacios probabilísticos son espacios medibles, y las variables aleatorias son precisamente funciones medibles en dichos espacios. Ahora hablaremos con toda generalidad, sin mencionar qué tipo de espacio medible es en el que estamos trabajando.
Un espacio de medida, recordamos, es una tríada (X,A,M), donde X es un conjunto cualquiera, A es una sigma-álgebra (la de los subconjuntos medibles) subre X y M es una medida definida en A.
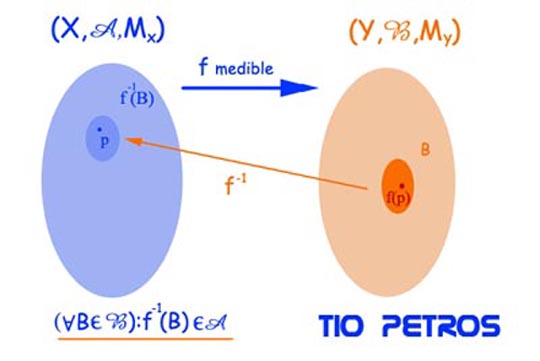
Supongamos que tenemos dos espacios de medida: (X,A,MX) y (Y,B,MY); y una aplicación f de X a Y. Diremos que f es una función medible cuando la antiimagen de todo subconjunto de Y que sea elemento de B es un subconjunto de X que es a su vez elemento de A.
De esta forma, la función “es respetuosa” con las sigma-álgebras de partida y de llegada.
Este aparente galimatías esconde una idea extremadamente sencilla: los elementos de las respectivas sigma-álgebras son simplemente aquellos subconjuntos para los cuales tiene sentido aplicar el concepto de medida, y por ello se denominan conjuntos medibles . La propiedad pedida a las funciones medibles exige que cada medible del conjunto de llegada tenga un alter ego medible en el conjunto de partida del cual es imagen por dicha aplicación.
Fijémonos en la figura: un punto p del espacio de partida tiene su imagen por la función f en el punto f(p) del espacio imagen. Dado un sunconjunto medible (con la medible definida en la imagen), existe otro medible en el origen (ahora con la medida definida en el espacio de origen) tal que es la contraimagen por la función f del primero.
Es fácil comprender que este tipo de funciones son las interesantes entre espacios medibles. Nuestra meta será definir una integral que sirva para todas las funciones medibles que se puedan construir en un espacio de medida.
El tipo más sencillo de funciones medibles es el de las funciones indicatrices.
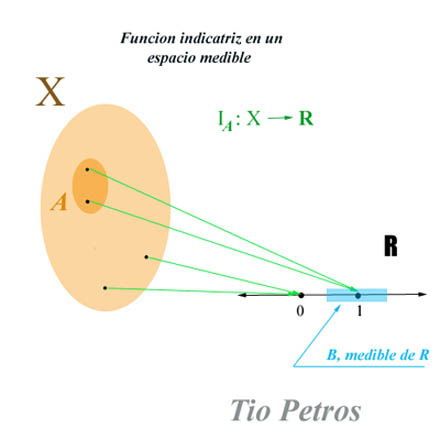
Una función indicatriz de un subconjunto no es sino una función que vale uno para todos los puntos de un subconjunto dado, valiendo cero para el resto. Es indicatriz de este subconjunto dado. Es importante señalar que la función no está definida sólo en dicho conjunto, sino en todo el espacio de partida.
Dado un subconjunto medible A de un conjunto medible X, la función indicatriz de A es:
IA(x)= 1 si x pertenece a A
IA(x)= 0 si x no pertenece a A
Demostremos que toda función indicatriz es medible:
La función indicatriz sólo toma dos valores, uno o cero. Dado un subconjunto B medible de R , que es el espacio de llegada, sólo pueden darse tres casos:
1.- que B contenga al uno y no al cero,
2.- que contenga al cero y no al uno,
3.- que contenga a ambos y
4.- que no contenga a ninguno.
En el primer caso, la contraimagen de B es precisamente A, porque por definición la contraimagen de B será el conjunto de todos aquellos puntos que toman valores en B, y de todos los posibles valores de B, sólo el uno tiene posibilidad de ser el valor asignado a puntos del origen. Como por definicion de la función indicatriz, los puntos que tienen asociado el valor unidad son los pertenecientes a A, tenemos el resultado. Razonando de la misma manera llegaremos a la conclusión de que en el segundo caso, la contraimagen de B es el complementario de A, en el tercero es el conjunto de origen entero y en el cuarto es el conjunto vacío. Todos ellos son conjuntos medibles por ser medible A, por lo que ya tenemos demostrado el resultado.
Continuaremos construyendo funciones más complicadas a partir de las indicatrices manteniendo la medibilidad de las mismas y definiendo la integral de Lebesgue enseguida.
Seguimos en breve.
7 comentarios
Fass Egos -
jose -
Jose Brox -
Aparte cuando consideras los distintos casos para la función indicatriz dices "hay tres casos" y luego describes cuatro xD
Jose Brox -
Magda -
Es interesante lograr que los estudiantes tengan curiosidad por la matemática.
Soy profesora universitaria en carreras de Economía y me cuesta enganchar a mis alumnos con el saber matemático
Felicitaciones, te visitaré a menudo.
Tio Petros -
Estamos hablando de un tipo de funciones muy general, de modo que es normal que al principio no quede claro del todo el concepto. Buscar funciones no medibles no es sencillo, precisamente porque queremos que bajo el concepto queden englobadas todas las funciones que puedan ser interesantes de algún modo, y poder integrarlas.
El ejemplo más claro de una función no medible es el de una función indicatriz de un subconjunto A no medible (¿ves porqué?). Es la existencia de conjuntos no medibles la que hace que existan funciones que no lo sean. Ahora la pregunta se traslada poner algún ejemplo de conjunto no medible. Hablaremos de ello en breve,te lo prometo.
Luisca -