Funciones simples
Viene de aquí.
Seguimos en nuestra intención de difinir un número cada vez más amplio de funciones que caigan dentro de lo que hemos definido como funciones medibles. Hemos visto que las funciones indicatrices son funciones medibles. Ahora utilizaremos aquellas para definir unas funciones, también medibles, que serán un poco más complejas que las indicatrices: las funciones simples.
Llamaremos función simple a toda función que tome un número finito de valores diferentes. Es fácil de comprender que las funciones simples se pueden expresar como combinación lineal de funciones indicatrices, por lo que adoptarán la siguiente forma general:
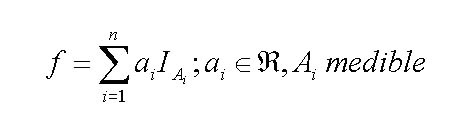
En la definición anterior no hemos especificado que los conjuntos Ai deban ser disjuntos, pero aunque no lo sean, toda función simple se puede poner como combinación lineal de funciones indicatrices de subconjuntos disjuntos, de modo que supondremos que lo son, sin pérdida de generalidad, y que forman un recubrimiento del espacio origen en su totalidad.
No demostraremos aquí, pero un resultado crucial que atañe a funciones medibles es que si f y g son dos funciones medibles, y c es una constante, entonces las funciones c.f, f+c, f+g, f.g, 1/f, max(f,g), min(f,g) y /f/ también son medibles.
En función de este resultado, las funciones simples serán medibles.
Será para estas funciones para las que definamos en primer lugar la integral de Legesgue, de la forma siguiente:

Así pues, definimos la integral de una función como una suma de productos. Cada producto está formado por el coeficiente correspondiente a cada subconjunto en la definición de la función y por la medida del mismo. Esto tiene enormes consecuencias: cualquier conjunto de medida cero, que influirá en las propiedades topológicas de la función y que incordiará mucho a la hora de integrar en el sentido de Riemann, aquí tiene un peso nulo en la integral, por lo que simplemente no será considerado. ¿Para qué íbamos a considerarlo, si está definido sobre un conjunto de medida nula?
Estaría bien reflexionar un poco sobre esta definición. Para empezar, la función de Dirichlet se convierte en integrable con ella, sin necesidad de mayor aparato matemático. Lo veremos en el siguiente post.
Posteriormente, como habíamos anunciado, veremos las excelentes propiedades de las funciones medibles, y la forma en que la definicion de la integral de Lebesgue se extiende a todas ellas.
3 comentarios
DIANA FAISURY -
Generic Cialis -
delfina tibur0na -