Mi primer "descubrimiento"
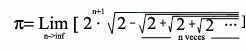 Fué con diecisiete años. Encontré una expresión de pi utilizando sólo doses. Como método de hallar el valor de pi no era gran cosa: estaba formada por dos factores, uno de ellos tendía a infinito y el otro lógicamente a cero, por lo que con cualquier sistema de cómputo la tendencia de los errores de redondeo a acumularse era enorme y daba al traste cualquier cálculo más allá del séptimo decimal. Pero la fórmula era cierta. Las matemáticas que utilicé (recuerden mis diecisiete años) eran lógicamente limitadas: trigonometría y cálculo de límites. Pero la sensación de triunfo fué inmensa. Me fuí creyendo poco a poco que mi "descubrimiento" era importante. La ilusión por aportar algo personal en matemáticas es una constante entre los aficionados, y rara vez se ve colmada por el éxito... mi caso no fué diferente: ¡se me habían adelantado!
Fué con diecisiete años. Encontré una expresión de pi utilizando sólo doses. Como método de hallar el valor de pi no era gran cosa: estaba formada por dos factores, uno de ellos tendía a infinito y el otro lógicamente a cero, por lo que con cualquier sistema de cómputo la tendencia de los errores de redondeo a acumularse era enorme y daba al traste cualquier cálculo más allá del séptimo decimal. Pero la fórmula era cierta. Las matemáticas que utilicé (recuerden mis diecisiete años) eran lógicamente limitadas: trigonometría y cálculo de límites. Pero la sensación de triunfo fué inmensa. Me fuí creyendo poco a poco que mi "descubrimiento" era importante. La ilusión por aportar algo personal en matemáticas es una constante entre los aficionados, y rara vez se ve colmada por el éxito... mi caso no fué diferente: ¡se me habían adelantado!El bueno de Arquímedes me había robado la gloria muchos siglos antes. Tardé años en ver mi fórmula en un libro de divulgación soviético, pero allá estaba. ¡El bueno de Arquímedes!.
La buena noticia es que nadie pudo quitarme el placer de "descubrir" por mí mismo algo que llevaba dos milenios y medio en poder de la comunidad matemática
14 comentarios
UlisesWainsteinHaimovichi -
Supra Vaider High -
UlisesWainsteinHaimovichi -
ROBERTO -
jairo -
otero -
NUEVA FORMULA PARA EL NUMERO PI
el metodo se basa en ir dividiendo en dos partes iguales un
triangulo rectangulo
Estos triangulos rectangulos contienen una circunferencia
en este caso toma como valor radio 1
Partiendo como valor inicial un triangulo rectangulo de 45
grados y lado 1 se itera la siguiente formula
2^(n + 2) * A[n]
en la que A[n] es igual a la formula iterativa
H[n] / ( 1 + ( 1 + H[n]^2 )^(1/2) )
en la que el valor inicial de H[n] es igual a 1.Este valor
inicial 1 es igual radio de la circunferencia.
Al ir dividiendo en dos partes iguales un triangulo rectangulo
sucesivamente averiguamos un valor determinado de la tangente
de un angulo que es resultado de dividir en partes iguales un
triangulo rectangulo inicial de 45 grados y lado 1 que multiplicado
por el numero de lados nos da una aproximacion sucesiva del
numero pi
para cualquier duda o consulta contactar con oteropera@hotmail.com
rosario -
Anónimo -
jose -
En los libros de dibujo técnico de secundaria que he consultado dan unas recetas para dibujar un óvalo, dado
a) el eje mayor,
b) el eje menor, o
c) ambos ejes,
y lo explican como si fuesen soluciones únicas. Quizá así pretendan ser pedagógicos (porque simplifican), pero a mí me parece un error: mostrar la solución general es igual de sencillo (es también una receta), y se enseña que los tres casos tienen infinitas soluciones.
¿Acaso tienen los autores miedo de que sean tantas?
Yo creo que así sólo logran ocultar la esencia perfumada y embriagadora de las matemáticas.
cero -
Hay otra cosa qeu todavia no se pq,que estudiando por qué la relacion entre el lado del un pentagono y el de la estrella inscrita en el da el numero aureo.Bien,lo que encontré esque es pq el seno72/sena36 es el numero aureo,mi pregunta es,pq esa fraccion da el numero aureo?
Enrique Blanco -
Yo soy músico, y en mi caso, inventé la escala octatónica unos 90 años después de Musorsgski, así qué algo puedo entender. Pero en realidad sólo escribo para agradecer la existencia y mantenimiento de esta bitácora, que he disfrutado mucho y a la que espero volver a menudo.
Lola -
Nicolas Bourbaki -
Tío Johnny -