Sangaku
Cuenta Julio A. Miranda Ubaldo que durante el Periodo EDO (1603-1867) Japón se encontraba aislado del mundo occidental, durante este periodo el acceso a todas las formas de cultura occidental y afluencia de ideas científicas occidentales fue suprimido con eficacia. En este periodo de la historia japonesa gente docta de todas las clases, desde comerciantes y granjeros hasta samurais(¿?) descubrían y solucionaban una amplia variedad de problemas geométricos, luego inscribían sus trabajos en tablillas de madera, (usando en muchos casos vivos colores) que después eran colgadas en las azoteas de santuarios shintoistas y templos budistas como una forma de agradecer a sus dioses. La palabra Sangaku significa algo así como tablilla matemática . Los problemas planteados en la tablillas Sangaku pueden perfectamente inscribirse en la matemática recreativa, y plantean endiablados problemas en los que aparecen invariablemente círculos tangentes unos a otros, o polígonos inscritos en otros polígonos y en círculos. También aparecen problemas con esferas tangentes a otras esferas, interior y exteriormente. Sin embargo no todos los problemas se ocupan sólo de la geometría, sino también de problemas aritméticos y algebraicos.
Rescato la siguiente información de la página de Julio A. Miranda Ubaldo:
El Sangaku más antiguo que sobrevive hasta hoy fue encontrado en la prefectura de Tochigi y es del año 1683.
Aunque muchos sangakus se han perdido o quemado todavía existen alrededor de 820 de estas tablillas.
Un notable investigador de los sangakus fue el matemático japonés Yoshio Mikami (1875-1950) quien en sus trabajos: "A history of Japanese mathematics" (Historia de las matematicas japonesas) de 1914 y "The Development of mathematics in China y Japon" (El Desarrollo de las Matemáticas en China y Japón) de 1974 realizó importantísimos estudios sobre estas tablillas matemáticas.
Hidetoshi Fukagawa es un matemático contemporáneo que ha viajado extensamente por todo el Japón para estudiar estas tablillas y tiene una prolífica colección de libros que se ocupan no sólo de los sangakus sino también de otros aspectos de las matemáticas japonesas.
En 1989 Fukagawa junto con Daniel Pedoe publicó un trabajo titulado "Japanese temple goemetry problems: Sangaku" que constituye la primera colección de sangakus en inglés.
Otros matemáticos japoneses como Tatsuhiko Kobayashi y Shigeyuki Takagi también han hecho contribuciones importantes al desarrollo de los problemas sangakus. Sin embargo no todos los problemas se ocupan sólo de la geometría, sino también de problemas aritméticos y algebraicos.
A modo de ilustración, vean ustedes estos dos bellísimos problemas:
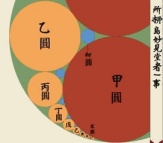
Dado un círculo (verde) de radio r con dos círculos menores interiores tangentes entre sí y tangentes tangentes al grande de radio r/2 (rojos), formamos un rosario de círculos (naranjas) tangentes cada uno al siguiente y a los círculos verde y rojo como se muestra en la figura. En los espacios intersticiales de la figura colocamos círculos tangentes a los tres círculos que delimitan el intersticio (azules). Encontrar el radio del enésimo círculo azul en función de r.
La resolución completa de este hermosísimo problema se encuentra (en inglés) aquí
_____________________________________________________________
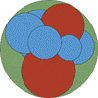
Este problema que data de 1822 está inscrito en una tablilla localizada en la prefectura de Kanagawa.
Dos esferas rojas son tangentes exteriormente y ambas son tangentes interiormente a la esfera grande de color verde. Un collar de esferas azules de diferentes tamaños rodea el "cuello" entre las esferas rojas. Cada esfera azul en el "collar" es tangente a sus vecinos próximos, a la vez que son tangentes a las dos esferas rojas y a la esfera verde.
¿Cuántas esferas azules conforman el collar?
¿Cómo los radios de las esferas azules se relacionan entre sí?
Pueden comprobar la magnitud de los problemas Sangaku, y también su extraordinaria belleza.
43 comentarios
Sabandre -
Isidoro -
Lomego -
Chico -
sexy black lesbian
free lesbian video trailer
fat black lesbian
free teen lesbian porn
lesbian strap on video
free lesbian porn trailer
black lesbian clip
black strap on lesbian
lesbian nude picture
black lesbian porn movie
asian lesbian video
lesbian having sex video
lesbian kiss video
Zamba -
Yocasta -
Nelia -
Fecha: 06/07/2006 19:35.
gravatar.com
Autor: Lizzy
Lizzy -
Peter -
AL -
Isabella -
Cristinne -
Mabel -
Ortino -
Blore -
James -
Jayor -
Pocho -
Macanno -
Milagro -
Jana -
Victor -
Chimmi -
Fey Arter -
Caracol -
Portada
Manni -
Geeni -
Cris -
Garrilo -
Divine -
Roque -
Natty -
Anetta -
Rose -
Macalla -
Jimmy -
Djenka -
Lauretta -
Jime -
redfre -
Ricardo -
Googleando he descubierto que el de 1974 es una segunda edición: «[...] 2nd edition, Chelsea Publ., New York, 1974. (1st ed. Leipzig, 1913.)»
Vailima -
1/r1+1/r4=1/r2+1/r5=1/r3+1/r6
un saludo
JuanPablo -