Blogia
Tio Petros

La proyección estereográfica de Riemann

- Conceptos
La proyección estereográfica de Riemann Un lector me pregunta por la equivalencia topológica entre la esfera y el plano. Intuitivamente, parece ser que ambas superficies no son equivalentes. Después de todo, la esfera es una superficie muy diferente a un plano; no sólo por su forma (cosa poco importante en topología) sino por propiedades globales, como acotamiento.
En efecto, ambas superficies son distintas a nivel topológico. Lo que ocurre es que basta con eliminar un punto a la esfera para que dejen de serlo.
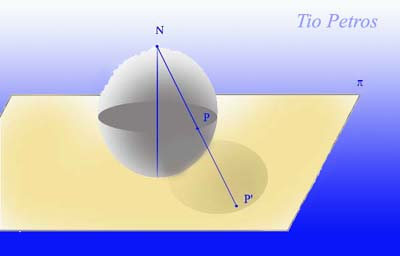
Supongamos una esfera descansando sobre un plano. Llamaremos punto S (sur) al único punto de contacto entre ambos, y punto N (norte) a la antípoda del punto S. Haremos corresponder cada punto P de la esfera con cada punto P’ del plano de la siguiente forma: unimos el punto N de la esfera con el punto P, y prolongamos la recta de unión hasta que corte al plano. Ese punto de corte es el punto P’, imagen de la proyección.
Es fácil darse cuenta de que cada punto de la esfera tiene su fiel reflejo en el plano, y viceversa; si exceptuamos el propio punto N, que no tiene correspondencia. Esta proyección se denomina proyección estereográfica de la esfera en el plano, o proyección de Riemann .
Los círculos de la esfera paralelos al ecuador se convierten en círculos en el plano con centro en el punto S, pero no se respetan las distancias (después de todo, la topología es lo que queda de la geometría cuando hemos suprimido la noción de distancia! ): cuanto mayor latitud norte tenga el paralelo, mayor es el radio del círculo proyectado en el plano. Un minúsculo paralelo muy cercano al punto N tendrá como reflejo un enorme círculo en el plano.
Un meridiano ( círculo máximo de la esfera que pasa por los puntos N y S, y es perpendicular al ecuador) se reflejará como una circunferencia degenerada en una recta que pasa por el punto S, y cualquier círculo máximo en la esfera intermedio se reflejará como una elipse más o menos excéntrica.
Ahora sí lo podemos decir: una esfera menos un miserable punto es topológicamente equivalente a un plano.

También podemos hacer que la esfera y el plano sean equivalentes de otra forma: en vez de eliminar un punto de la esfera, añadimos un punto al plano. Parece una estupidez añadir un punto a un plano (¿Dónde lo ponemos?) Sin embargo, no lo es. Se puede definir perfectamente un "punto en el infinito" que será el reflejo (a estas alturas espero que lo hayan adivinado) del puñetero punto N de la esfera; el único que quedaba sin emparejar. Esta construcción se denomina compactificación del plano mediante la adición de un punto en el infinito.

29 comentarios

victor -

tienes alguna explicación de cómo termino la geometría de riemann, convertida en geometría esférica. Por que el en su trabajo habla de una métrica para superficies en espacios n-dimensionales.

Air Force Ones -

Every day is blue day. If you encounter a setback, please look up to the sky, if only the sky is blue, you don't lose the hope.

Jordan Spizikes -

The answer is extremely straightforward. It is allin how they understand their troubles. Yes, each and every dwelling person has problems. A problem-free existence is an illusion-a mirage inside the desert. Accept that fact.

María josé -

muy buen tema

Tadalafil -

Yo necesito saber cual es la equivalencia topologica entre es una esfera y un plano ya que estoy estudiando astronomia.

S. Amoretty H. -

la informacion encontarda es buena!, me gustaria aprender a proyectar diferentes tipos de figuras geométracas, a treves de la proyección estereografica

Samuel Amoretty -

como se proyecta un plano, el traingulo, cuadrado, linea u otra figura, a travez de la proccion de Rieman

juan -

alguien me podria ayudar a enteder la proyeccion estereografica o algun sitio donde pueda investigar sobre el mismo

aJ -

dios, cuanto friki!

Isi-TioTaum -

Cuanto mas, curioso, curioso

cesar -

necesito hacer un trabajo de proyeccion estereografica de los puntos de una esfera sobre un plano y viceversa pero ocupo un programa que me haga poder explicarlo de manera dinamica, si alguien puede ayudarme, le estoy nuy agradecido.

gustavo -

disculpen mi ignorancia,pero porque se toma al punto N como equivalencia del infinito?

otroIgnorante -

Qué curioso, yo también he llegado aquí porque no entiendo la explicación de Penrose en su libro, y también me ha ayudado bastante

ben. -

estoy leyendo a penrose " el camino de la realidad" y no le entiendo casi nada. lo que acabo de encontrar aquí me da un poco de luz en la tiniebla de mi ignorancia

oscar martinez -

muy buenos comentarios pero tengo una inquietud como se demostraria la biyeccion entre la esfera y el plano

Zero_Mat -

Es interesante todo lo que trataban de dar a entender, pero el problema de la proyeccion estereografica de riemman no termina hay.
hace un par de dias compartia con unos compañeros informacion sobre diche tema.
Ahora supongan que la esfera esta como se trata en variable compleja, o sea que el plano corta a la esfera en el ecuador, y no en el punto S, antes mensionado.
Esto quiere decir que si la relacion que hay entre el polo Norte (punto N) y cualquier punto de la esfera P se refleja en el plano.
Bueno lo interesante es que si existen el mismo numero de puntos en la parte inferior como en la parte superior de la esfera entonces el numero de puntos reflejados dentro como fuera de la esfera en el plano deverian de ser iguales. lo cual deja no muy claro este consepto ya que la esfera tiene como condicien que es una esfera unitaria. y por lo tanto no puede de ninguna forma haber el mismo numero de puntos dentro como fuera de ella.

Roberto Quiñones -

Me interesa compatir ideal sobre la proyeccion estereografica.

daniela -

bobos

JAIR VALLE -

VIVO EN BRAZIL
SOY ESTUDIANTE DE MATEMATICA
ME GUSTA LA GEOMETRIA ESFERICA

- LOBACHEVISKI

- RIEMANN

Y OTROS

ME GUSTO ENCONTRAR TU TRABAJO

QUIERO APRENDER MUCHO SOBRE GEOMETRIAS.

SUERTE
J.

victor montilva -

por favor necesito informaciòn sobre geometria esferica, soy estudiante de matemaicasde la ULA en Mèrida - venezuela y aca no vemos geometria esfèrica como materia, es decir no la estudiamos, sin embargo necesito hacer untrabajo muy importante de geometria esferica, pero en la universidad no hay informacion, por favor, necesito ayuda

Crystal -

Me alegro de haber entendido por fin la dichosa proyección de Riemann (se me ocurrió faltar justo ese día clase...), ahora todos mis conocimientos de variable compleja se reordenan de forma casi mágica.

Gracias, Tio Petros!

Félix -

Qué recuerdos de mis días estudiando Variable Compleja. Apenas quedan vagos recuerdos de aquello... La figura que aquí nos muestras es uno de ellos. Otro creo que tenía que ver con Planos de Riemann...

Carlos -

Está claro, al insertar el nuevo punto si quieres que el nuevo espacio sea compacto, tienes que contruir una nueva topología T* que haga que el espacio X* sea compacto. Lo que se hace en sentido abstracto es construir una nueva base de abiertos B= T U { {p}U (X-L): L compacto en (X,T)}. De aqui ya construimos T*. Y por eso surge de forma natural un nuevo entorno de {p} que tu decias, que es precisamente B(p)= {{p}U(X-L): L compacto en (X,T)}. Lo que pasa, de aqui, como le das un sentido geométrico de que el punto está en el infinito ???

Tio Petros -

Vale. Entre Fernand0 y Rimblow me habeis convencido. Además, ese viaje aunque infinito, no tiene pérdida: cualquier dirección es la buena!!!

rimblow -

Estoy de acuerdo totalmente con Fernand0, y creo que el punto N, es con el que me quedo, ya que hay que ir hasta el infinito para buscar su punto en el plano, y me parece un viaje fascinante, por que su camino es mayor....

Tio Petros -

Para Fernand0: Es verdad, tan miserable no puede ser... sin embargo, todos los puntos de la esfera tienen la misma potencialidad, con lo que tampoco se le deben subir excesivamente los humos a nuestro {p}. :)

Para Carlos:Es exactamente como dices, Carlos. Sin embargo, además de añadir el punto {p} hay que definir correctamente una base de entornos del "nuevo" punto {p} que añadimos para tener compactificado el espacio topológico ampliado. Esa base de entornos es la que nos legitima visualizar dicho punto como un punto en el infinito, pero en espacios más generales no tendrá interpretación geométrica (en el sentido clásico del término) alguna, y funcionará igual de bien.

Carlos -

Esto de la compactificación por un punto o de Alexandrov, fijate que casualidad que lo estuvimos dando la pasada semana en clase, evidentemente, desde un punto de vista más abstracto y general, para cualquier espacio topológico (X,T). El caso es que añadir un punto, realmiente tiene que tener un sentido geométrico, es decir, que esté en el infinito ? Yo creo que no es necesario, que esa es una interpretación para hacerlo más intuitivo. Yo opino, si tengo un espacio (X,T) , construyo X*=XU{p}donde p es un punto que no está dentro de el espacio topológico. Si X=R^3, pues vale, añadimos un punto que no está en R^3, no hace falta verle ningun sentido geométrico, solo topológico, en términos de espacio como conjunto. Me parece que esto da mucha potencia, aunque entiendo que se intente hacer mas intuitivo, resulta menos impactante y ahuyenta menos a la gente que no esta metida en esto.

Un Saludo.

fernand0 -

No puede ser miserable alguien que marca semejante diferencia!

;)

Shunt -

¡Fascinante! Se le denomina también punto impropio, ¿no? Parece mentira que sea común a cualquier recta del plano, sin importar la dirección. Gracias por la explicación. También se me ocurre si, topológicamente hablando, daría igual estar dentro de una esfera hueca que estar fuera.